24 г.Йошкар-Олы»
учитель математики
Горлова М.Х.
- Главная
- Разное
- Образование
- Спорт
- Естествознание
- Природоведение
- Религиоведение
- Французский язык
- Черчение
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, фоны, картинки для презентаций
- Экология
- Экономика
Презентация, доклад к уроку геометрии в 10 классе Теорема о трех перпендикулярах
Содержание
- 1. Презентация к уроку геометрии в 10 классе Теорема о трех перпендикулярах
- 2. ТЕМА УРОКА: РАССТОЯНИЕ ОТ ТОЧКИ ДО ПЛОСКОСТИ. ТЕОРЕМА О ТРЕХ ПЕРПЕНДИКУЛЯРАХ.
- 3. Цели урока:Ввести понятие расстояния от точки до
- 4. Актуализация опорных знанийУгол между прямыми равен 90
- 5. Перпендикуляр к плоскости, наклонная, проекция наклонной на
- 6. Слайд 6
- 7. Расстояние между параллельными плоскостямиРасстоянием между параллельными плоскостями
- 8. Расстояние между прямой и плоскостью, расстояние между
- 9. Расстояние между скрещивающимися прямымиα || β, а
- 10. Теорема о трех перпендикулярах Прямая, проведенная
- 11. Решение задач. Задача 1Через вершину А
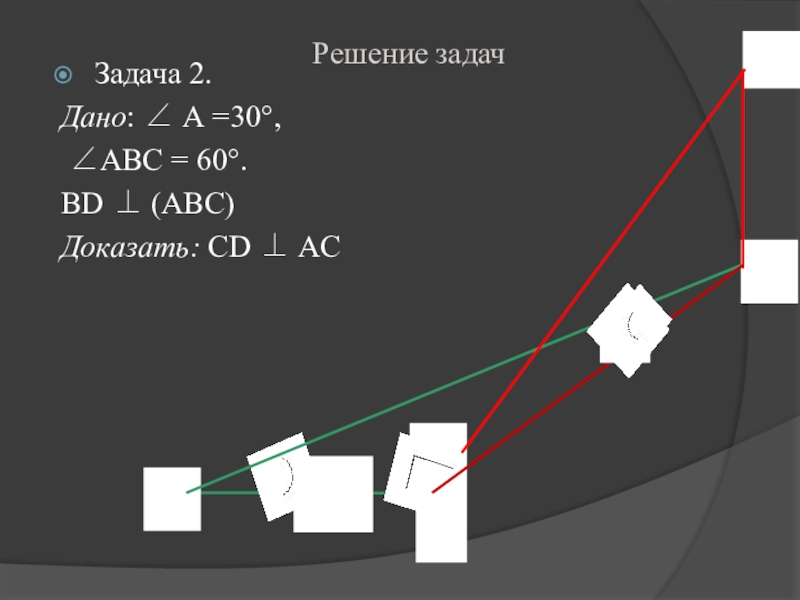
- 12. Решение задачЗадача 2.Дано: ∠ А =30°, ∠АВС = 60°. ВD ⊥ (АВС) Доказать: СD ⊥ АC
- 13. Домашнее задание:Пункты 19, 20.Самостоятельно – обратную теорему.Решить задачи № 140, 143.
- 14. Список литературы: 1. Геометрия: Учеб. Для
ТЕМА УРОКА: РАССТОЯНИЕ ОТ ТОЧКИ ДО ПЛОСКОСТИ. ТЕОРЕМА О ТРЕХ ПЕРПЕНДИКУЛЯРАХ.
Слайд 1Название презентации:
Теорема о трех перпендикулярах
геометрия 10 класс
МБОУ «Средняя общеобразовательная школа №
Слайд 3Цели урока:
Ввести понятие расстояния от точки до плоскости ;
Доказать теорему о
трех перпендикулярах. Показать применение этой теоремы при решении задач.
Слайд 4Актуализация опорных знаний
Угол между прямыми равен 90 ⁰. Как называются такие
прямые?
Верно ли утверждение: «Прямая называется перпендикулярной плоскости, если она перпендикулярна некоторой прямой, лежащей в этой плоскости»?
Что можно сказать о двух прямых, перпендикулярных к одной плоскости?
Две прямые, перпендикулярные третьей прямой, ….
Как определяется расстояние от точки до прямой на плоскости?
Как определить расстояние от точки до плоскости?
Верно ли утверждение: «Прямая называется перпендикулярной плоскости, если она перпендикулярна некоторой прямой, лежащей в этой плоскости»?
Что можно сказать о двух прямых, перпендикулярных к одной плоскости?
Две прямые, перпендикулярные третьей прямой, ….
Как определяется расстояние от точки до прямой на плоскости?
Как определить расстояние от точки до плоскости?
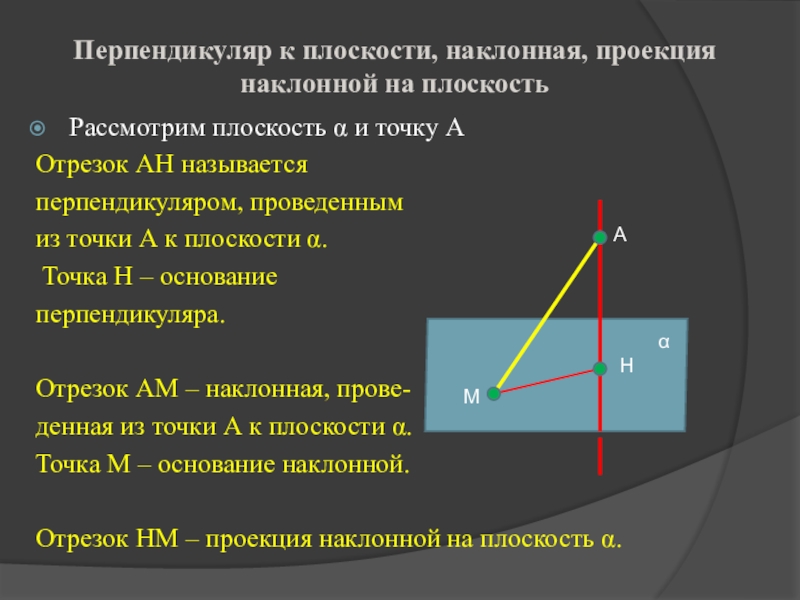
Слайд 5Перпендикуляр к плоскости, наклонная, проекция наклонной на плоскость
Рассмотрим плоскость α и
точку А
Отрезок АН называется
перпендикуляром, проведенным
из точки А к плоскости α.
Точка Н – основание
перпендикуляра.
Отрезок АМ – наклонная, прове-
денная из точки А к плоскости α.
Точка М – основание наклонной.
Отрезок НМ – проекция наклонной на плоскость α.
Отрезок АН называется
перпендикуляром, проведенным
из точки А к плоскости α.
Точка Н – основание
перпендикуляра.
Отрезок АМ – наклонная, прове-
денная из точки А к плоскости α.
Точка М – основание наклонной.
Отрезок НМ – проекция наклонной на плоскость α.
А
Н
М
α
Слайд 6
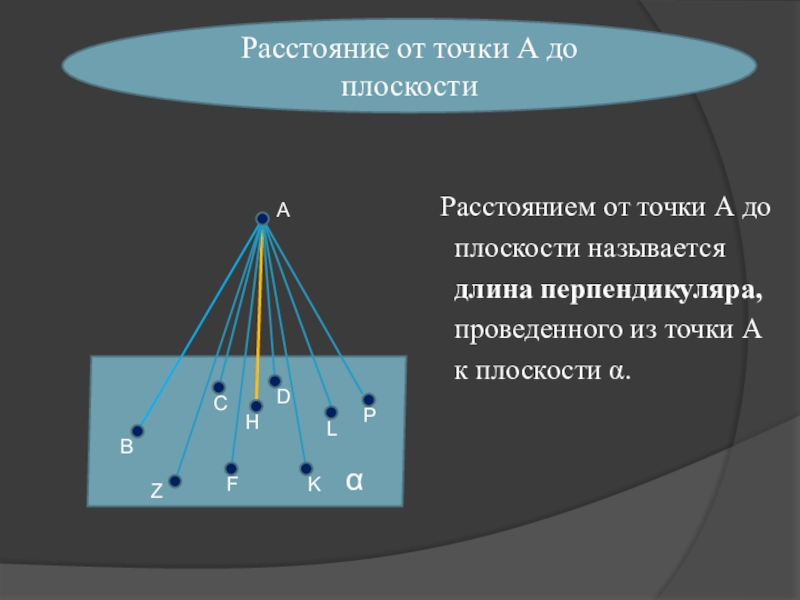
Расстоянием от точки А до
плоскости называется
длина перпендикуляра,
проведенного из точки А
к плоскости α.
А
В
С
D
H
L
P
K
F
Z
Расстояние от точки А до плоскости
α
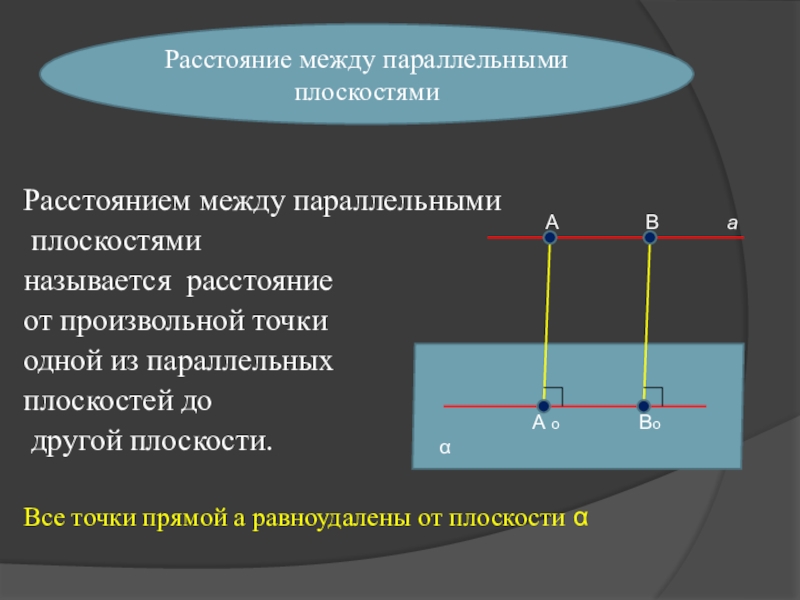
Слайд 7Расстояние между параллельными плоскостями
Расстоянием между параллельными
плоскостями
называется расстояние
от произвольной точки
одной из параллельных
плоскостей до
другой плоскости.
Все точки прямой а равноудалены от плоскости α
А
В
А о
Во
α
а
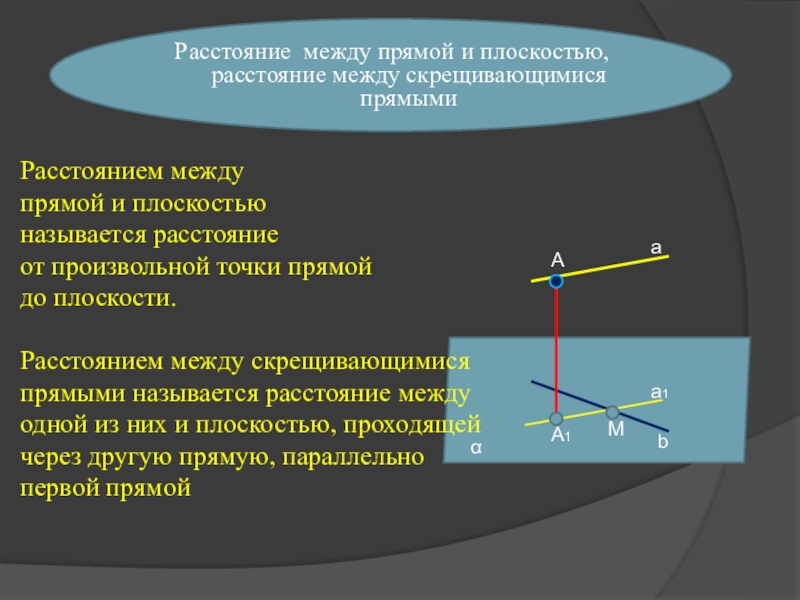
Слайд 8Расстояние между прямой и плоскостью, расстояние между скрещивающимися прямыми
А
А1
М
b
a
a1
α
Расстоянием между
прямой
и плоскостью
называется расстояние
от произвольной точки прямой
до плоскости.
Расстоянием между скрещивающимися прямыми называется расстояние между одной из них и плоскостью, проходящей через другую прямую, параллельно первой прямой
называется расстояние
от произвольной точки прямой
до плоскости.
Расстоянием между скрещивающимися прямыми называется расстояние между одной из них и плоскостью, проходящей через другую прямую, параллельно первой прямой
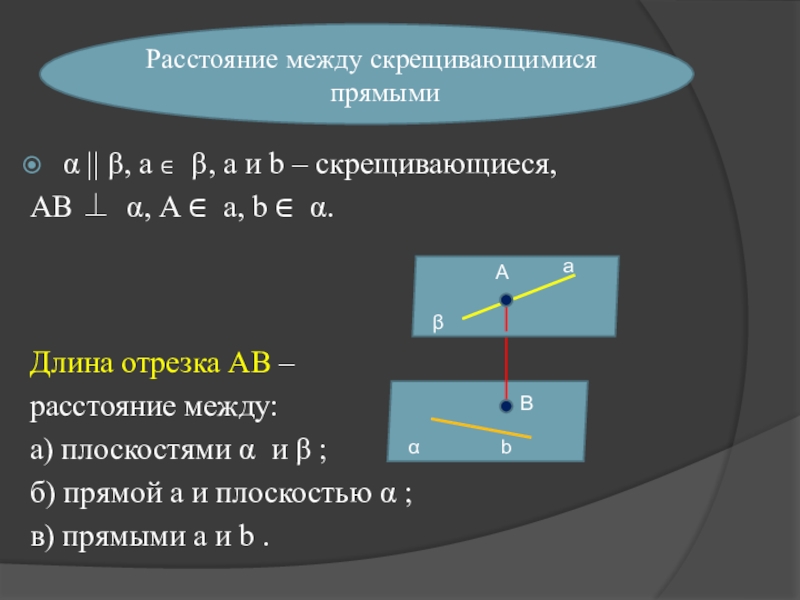
Слайд 9Расстояние между скрещивающимися прямыми
α || β, а ∈ β, а
и b – скрещивающиеся,
АВ ⊥ α, А ∈ а, b ∈ α.
Длина отрезка АВ –
расстояние между:
а) плоскостями α и β ;
б) прямой а и плоскостью α ;
в) прямыми а и b .
АВ ⊥ α, А ∈ а, b ∈ α.
Длина отрезка АВ –
расстояние между:
а) плоскостями α и β ;
б) прямой а и плоскостью α ;
в) прямыми а и b .
А
В
а
b
α
β
Слайд 10Теорема о трех перпендикулярах
Прямая, проведенная в плоскости через основание
наклонной перпендикулярно к ее проекции на эту плоскость, перпендикулярна и к самой наклонной
Дано: АН ⊥ α, АМ – наклонная к
плоскости α, НМ – проекция наклонной,
а ∈ α, а ⊥ НМ.
Доказать: а ⊥ АМ.
Доказательство: Т.к. АН ⊥ α,
то АН ⊥ а ⇒ а ⊥ β ⇒ а ⊥ АМ.
Три перпендикуляра: AH, НМ, АМ
Дано: АН ⊥ α, АМ – наклонная к
плоскости α, НМ – проекция наклонной,
а ∈ α, а ⊥ НМ.
Доказать: а ⊥ АМ.
Доказательство: Т.к. АН ⊥ α,
то АН ⊥ а ⇒ а ⊥ β ⇒ а ⊥ АМ.
Три перпендикуляра: AH, НМ, АМ
А
Н
М
а
α
β
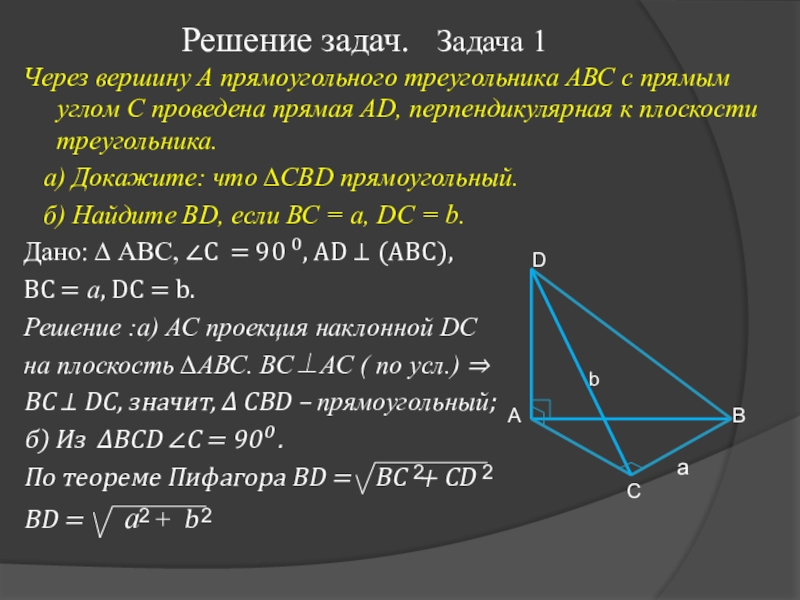
Слайд 11Решение задач. Задача 1
Через вершину А прямоугольного треугольника АВС с
прямым углом С проведена прямая AD, перпендикулярная к плоскости треугольника.
а) Докажите: что ∆CBD прямоугольный.
б) Найдите BD, если ВС = а, DC = b.
Дано: ∆ АВС, ∠С = 90 ⁰, AD ⊥ (ABC),
ВС = а, DC = b.
Решение :а) АС проекция наклонной DC
на плоскость ∆АВС. ВС⊥АС ( по усл.) ⇒
ВС ⊥ DС, значит, ∆ CBD – прямоугольный;
б) Из ∆ВСD ∠С = 90⁰ .
По теореме Пифагора BD = ВС + CD
ВD = а + b
а) Докажите: что ∆CBD прямоугольный.
б) Найдите BD, если ВС = а, DC = b.
Дано: ∆ АВС, ∠С = 90 ⁰, AD ⊥ (ABC),
ВС = а, DC = b.
Решение :а) АС проекция наклонной DC
на плоскость ∆АВС. ВС⊥АС ( по усл.) ⇒
ВС ⊥ DС, значит, ∆ CBD – прямоугольный;
б) Из ∆ВСD ∠С = 90⁰ .
По теореме Пифагора BD = ВС + CD
ВD = а + b
А
В
С
D
b
2
2
2
2
a
Слайд 14Список литературы:
1. Геометрия: Учеб. Для 10-11 кл. сред. шк./
Л.С. Атанасян,
В.Ф. Бутузов, С.Б. Кадомцев.
2. Поурочные разработки по геометрии: 10 класс/ Сост.
В.А. Яровенко. – М.: ВАКО, 2011.
В.Ф. Бутузов, С.Б. Кадомцев.
2. Поурочные разработки по геометрии: 10 класс/ Сост.
В.А. Яровенко. – М.: ВАКО, 2011.