Презентация, доклад к уроку геометрии в 10 классе Углы в пространстве

МКОУ «Островская СОШ» учитель математики Варёшина Елена Александровна

Урок изучение нового материала.

Урок геометрии в 10 классе
На тему «Углы в пространстве»

Геометрия есть искусство правильно рассуждать на неправильных чертежах. Д. Пойа.

Изучая геометрию в пространстве много нового узнали мы. Параллельность плоскостей, и их пересечение. А сегодня тема про углы.

Тема урока:
Угол между скрещивающимися прямыми.
Угол между прямой и плоскостью.
Угол между плоскостями.

Мы поставим цель урока, всё по пунктикам разложим, все понятия изучим. А потом всё подытожим.

. 1.Повторить всё, что изучено в планиметрии про углы.
2.Изучить новые определения, замечания.
3. Рассмотреть задачи на применение новых понятий.
4. Научиться решать, делать соответствующие чертежи и оформлять решение.

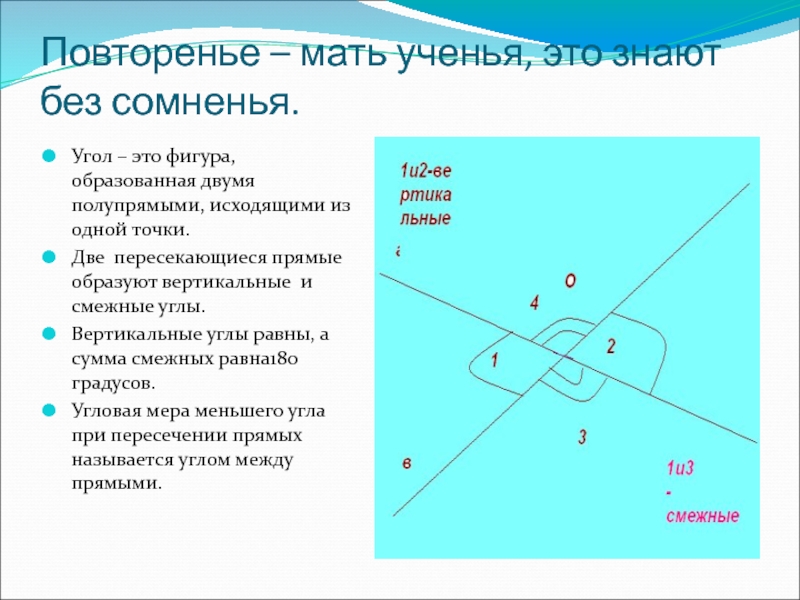
Повторенье – мать ученья, это знают без сомненья.

Угол – это фигура, образованная двумя полупрямыми, исходящими из одной точки.
Две пересекающиеся прямые образуют вертикальные и смежные углы.
Вертикальные углы равны, а сумма смежных равна180 градусов.
Угловая мера меньшего угла при пересечении прямых называется углом между прямыми.

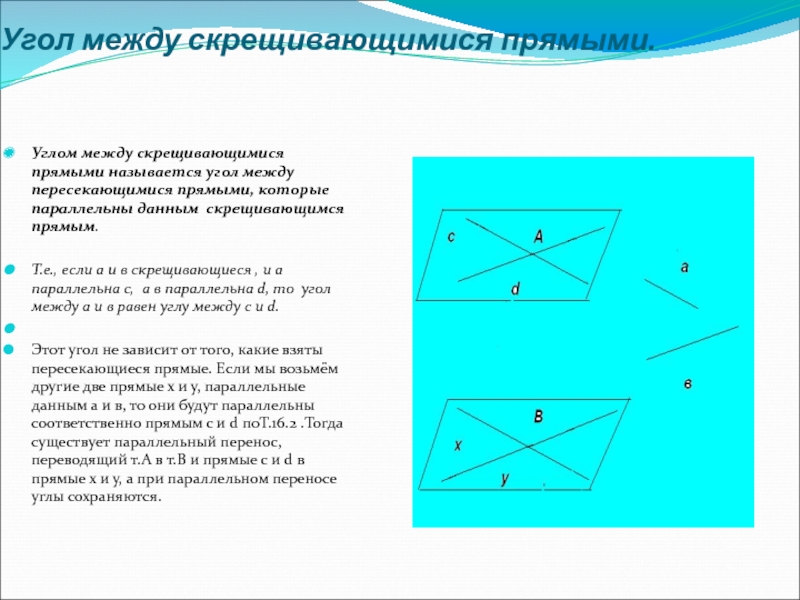
Угол между скрещивающимися прямыми.

Углом между скрещивающимися прямыми называется угол между пересекающимися прямыми, которые параллельны данным скрещивающимся прямым.

Т.е., если а и в скрещивающиеся , и а параллельна с, а в параллельна d, то угол между а и в равен углу между с и d.

Этот угол не зависит от того, какие взяты пересекающиеся прямые. Если мы возьмём другие две прямые х и у, параллельные данным а и в, то они будут параллельны соответственно прямым с и d поТ.16.2 .Тогда существует параллельный перенос, переводящий т.А в т.В и прямые с и d в прямые х и у, а при параллельном переносе углы сохраняются.

Понятие узнали, имеем представление и надо рассмотреть нетрудное решение.

З а д а ч а.
Докажите, что любая прямая на плоскости перпендикулярная проекции наклонной на эту плоскость, перпендикулярна и наклонной.
Дано:
АВ - перпендикуляр.
АС - наклонная
ВС – проекция.
у – прямая плоскости j, перпендикулярна ВС
Доказать, что у перпендикулярна АС.
Доказательство:
1. Проведем через т. С прямую х параллельную у.
2.. По теорем о трёх перпендикулярах х перпендикулярна АС.
3. Т.к. угол между х и АС равен углу между у и АС, то у и АС перпендикулярны.

Угол между прямой и плоскостью.

Углом между прямой и плоскостью называется угол между прямой и проекцией этой прямой на плоскость.
Х – данная плоскость.
а – прямая, пересекающая эту плоскость.
в – проекция этой прямой.
Z – угол между прямой и плоскостью.

Мы должны задачу решить, синусы, косинусы повторить.

Найти длины наклонных, проведенных из точки А к плоскости под углами 30, 45, 60 градусов, если т. А отстоит от плоскости на расстояние 6 сантиметров.

Решение:
1. Проведём из точки А перпендикуляр на плоскость у.
2. Построим проекцию наклонной АВ - ВС.
3. Найдём АВ как гипотенузу прямоугольного треугольника: катет разделим на синус противолежащего угла.

Угол между плоскостями.

Пусть две плоскости v и jпересекаются. Проведём плоскость g, перпендикулярную линии их пересечения с. Она пересечёт их по прямым а и в.
Угол между этими прямыми а и в называют углом между данными плоскостями vи j.

Что бы определение закрепить надо также задачку решить.

Даны две пересекающиеся плоскости под углом 30 градусов. Точка А лежащая в одной из этих плоскостей отстоит от другой на расстоянии 4 сантиметра. Найти расстояние от этой точки до линии пересечения этих плоскостей.

Задачу решили мы, построили все в ней углы, но надо проверить решение, а так же её оформление

Дано:
Угол АСВ =30 градусов.
АВ = 4 сантиметра.
АС - ?
Решение:
АС =4 : sin 30 = 8
Ответ: АС 8 сантиметров.

Подведем итог урока. Поработали неплохо. Изучили мы углы, очень сложные они.

Углом между скрещивающимися прямыми называется угол между пересекающимися прямыми, которые параллельны данным скрещивающимся прямым.
Углом между прямой и плоскостью называется угол между прямой и проекцией этой прямой на плоскость.
Углом между двумя плоскостями называется угол, образованный двумя прямыми, полученными при пересечении этих плоскостей третей, перпендикулярной линии их пересечения.

Геометрия в жизни пригодится, поэтому надо ребята учиться.

Теорию изучать, задачек как можно больше решать и решать.