- Главная
- Разное
- Образование
- Спорт
- Естествознание
- Природоведение
- Религиоведение
- Французский язык
- Черчение
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, фоны, картинки для презентаций
- Экология
- Экономика
Презентация, доклад к уроку геометрии
Содержание
- 1. Презентация к уроку геометрии
- 2. Треугольник – это многоугольник с тремя сторонами
- 3. Если все три угла острые ( рис.20
- 4. Треугольник ABC ( рис.23 ) - равнобедренный,
- 5. 1. Против большей стороны лежит больший угол,
- 6. 4. Продолжая одну из сторон треугольника (AC,
- 7. Треугольники равны, если у них соответственно равны:
- 8. Два прямоугольных треугольника равны, если выполняется одно
- 9. Высота треугольника - это перпендикуляр, опущенный из
- 10. Медиана – это отрезок, соединяющий любую вершину
- 11. Срединный перпендикуляр – это перпендикуляр, проведенный из
Слайд 2Треугольник – это многоугольник с тремя сторонами (или тремя углами). Стороны
Треугольник
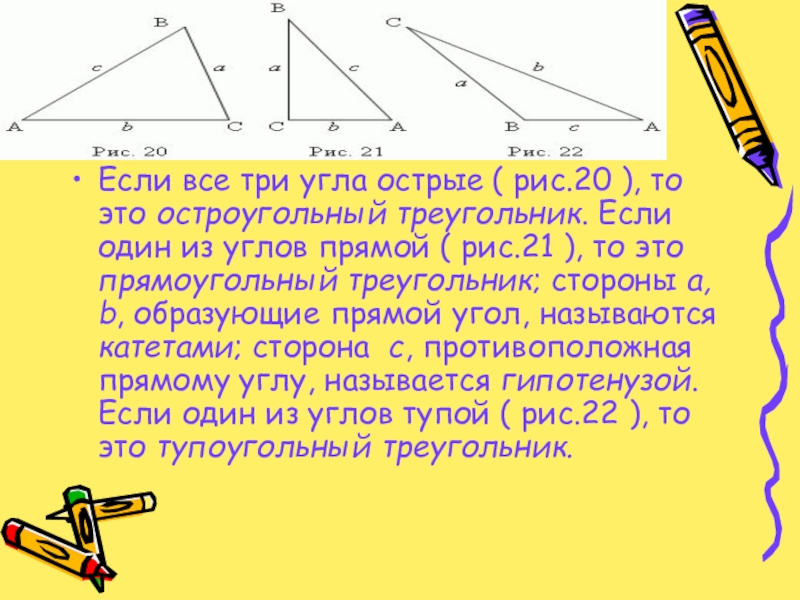
Слайд 3Если все три угла острые ( рис.20 ), то это остроугольный
Слайд 4Треугольник ABC ( рис.23 ) - равнобедренный, если две его стороны
Слайд 51. Против большей стороны лежит больший угол, и наоборот.
2. Против равных
В частности, все углы в равностороннем треугольнике равны.
3. Сумма углов треугольника равна 180 º .
Из двух последних свойств следует, что каждый угол в равностороннем треугольнике равен 60 º.
Основные свойства треугольников
Слайд 64. Продолжая одну из сторон треугольника (AC, рис.25), получаем внешний угол
5. Любая сторона треугольника меньше суммы двух других сторон и больше их разности ( a < b + c, a > b – c; b < a + c, b > a – c; c < a + b, c > a – b ).
Слайд 7Треугольники равны, если у них соответственно равны:
b) два угла и прилегающая к ним сторона;
c) три стороны.
Признаки равенства треугольников
Слайд 8Два прямоугольных треугольника равны, если выполняется одно из следующих условий:
1) равны
2) катет и гипотенуза одного треугольника равны катету и гипотенузе другого;
3) гипотенуза и острый угол одного треугольника равны гипотенузе и острому углу другого;
4) катет и прилежащий острый угол одного треугольника равны катету и прилежащему острому углу другого;
5) катет и противолежащий острый угол одного треугольника равны катету и противолежащему острому углу другого.
Признаки равенства прямоугольных треугольников
Слайд 9Высота треугольника - это перпендикуляр, опущенный из любой вершины на противоположную
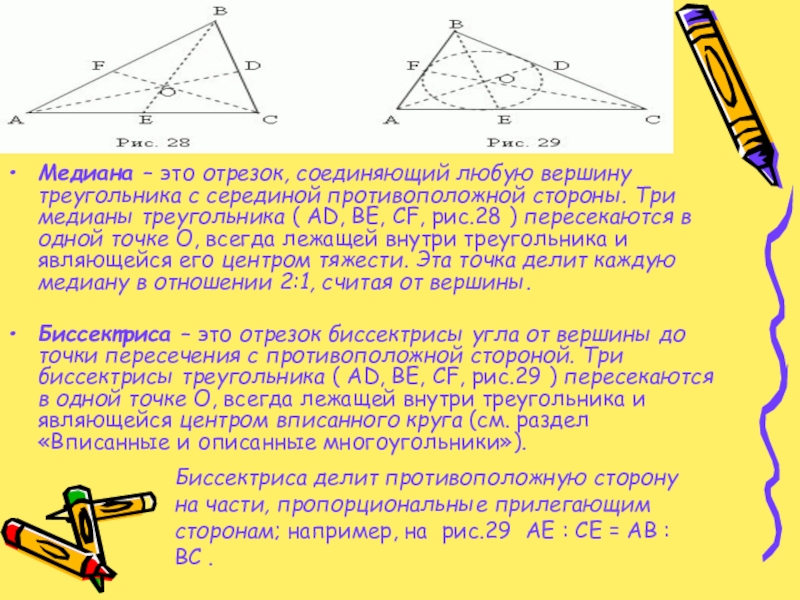
Слайд 10Медиана – это отрезок, соединяющий любую вершину треугольника с серединой противоположной
Биссектриса – это отрезок биссектрисы угла от вершины до точки пересечения с противоположной стороной. Три биссектрисы треугольника ( AD, BE, CF, рис.29 ) пересекаются в одной точке О, всегда лежащей внутри треугольника и являющейся центром вписанного круга (см. раздел «Вписанные и описанные многоугольники»).
Биссектриса делит противоположную сторону на части, пропорциональные прилегающим сторонам; например, на рис.29 AE : CE = AB : BC .
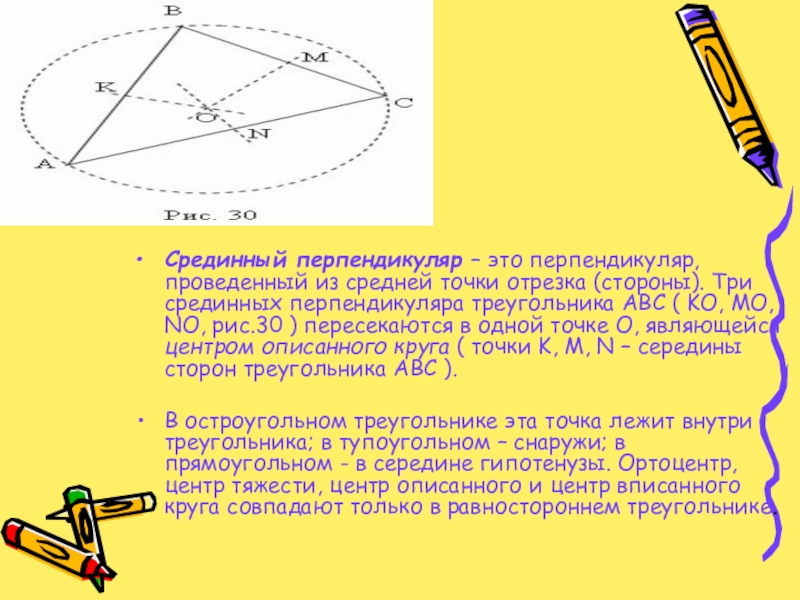
Слайд 11Срединный перпендикуляр – это перпендикуляр, проведенный из средней точки отрезка (стороны).
В остроугольном треугольнике эта точка лежит внутри треугольника; в тупоугольном – снаружи; в прямоугольном - в середине гипотенузы. Ортоцентр, центр тяжести, центр описанного и центр вписанного круга совпадают только в равностороннем треугольнике.