- Главная
- Разное
- Образование
- Спорт
- Естествознание
- Природоведение
- Религиоведение
- Французский язык
- Черчение
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, фоны, картинки для презентаций
- Экология
- Экономика
Презентация, доклад к уроку геометрии (10 класс, Атанасян)
Содержание
- 1. Презентация к уроку геометрии (10 класс, Атанасян)
- 2. Проверка домашнего задания
- 3. Дайте определение призмы.Какую призму называют правильной?Площадь боковой
- 4. Математический диктантВерно ли, что куб является правильной
- 5. Математический диктантОпределите количество сторон многоугольника, лежащего в
- 6. «Что может быть больше похоже на мою
- 7. Симметрия в пространстве. Правильные многогранники
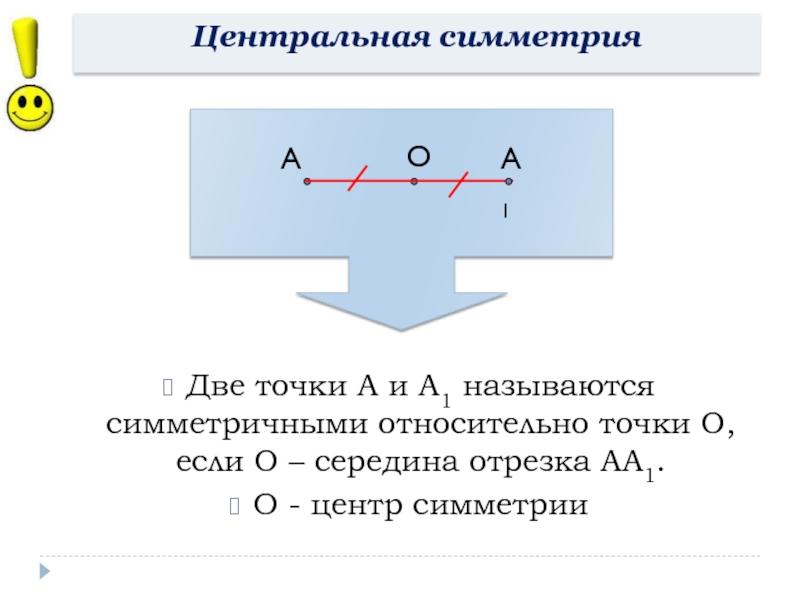
- 8. Центральная симметрияДве точки А и А1 называются
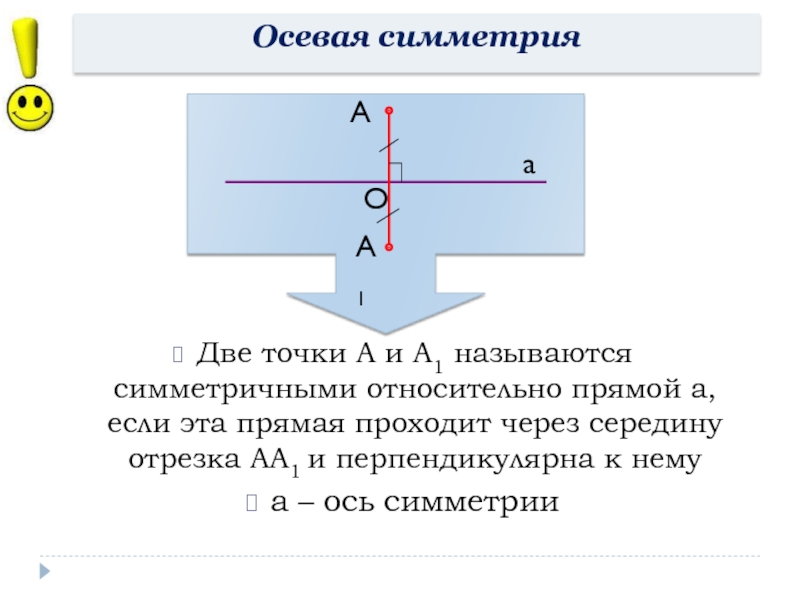
- 9. Осевая симметрияДве точки А и А1 называются
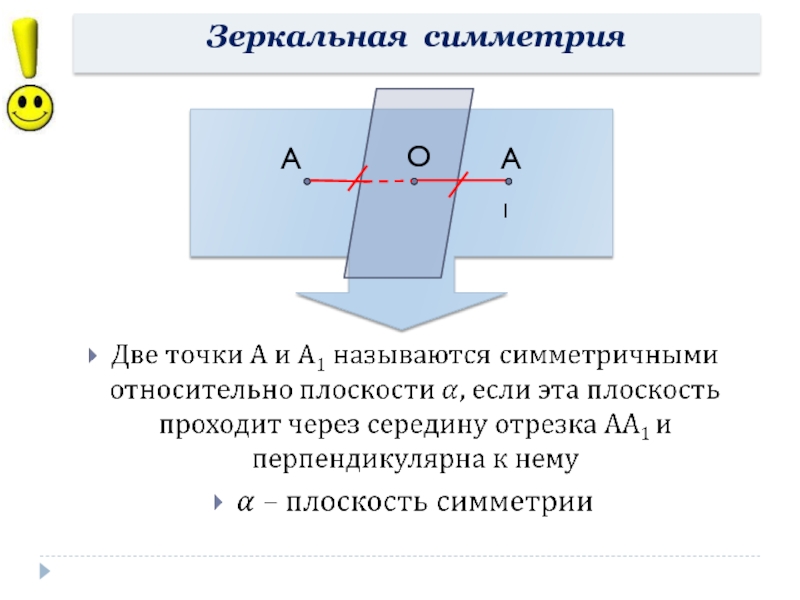
- 10. Зеркальная симметрияАОА1
- 11. Энантиоморфы – это пара зеркально асимметричных объектов
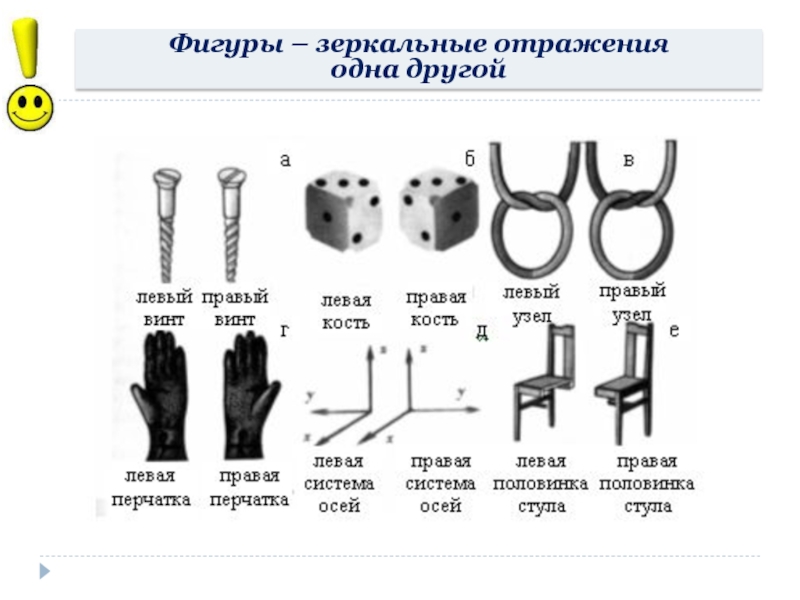
- 12. Фигуры – зеркальные отражения одна другой
- 13. Зеркальная симметрия (ее ещё называют
- 14. Двуглавый орел хорошо послужил государству Российскому как
- 15. Изображения на плоскости многих предметов окружающего нас
- 16. Центральная, осевая симметрия в окружающем мире
- 17. Фигуры, обладающие осевой, зеркальной симметрией
- 18. Слайд 18
- 19. Существуют пять видов правильных выпуклых многогранников (тела
- 20. пришли из Древней Греции, в них указывается
- 21. Что такое правильный многогранник?Правильных многогранников вызывающе мало,
- 22. Правильные многогранники иногда
- 23. «Космический кубок» Кеплера Кеплер
- 24. Правильный тетраэдр Составлен из четырёх равносторонних
- 25. Правильный тетраэдр
- 26. Правильный октаэдрСоставлен из восьми равносторонних треугольников. Каждая
- 27. Правильный икосаэдрСоставлен из двадцати равносторонних треугольников. Каждая
- 28. Составлен из шести квадратов. Каждая
- 29. Куб
- 30. Правильный додекаэдр Составлен из двенадцати правильных пятиугольников.
- 31. Правильного многогранника, гранями которого являются правильные шестиугольники,
- 32. Определите количество граней, вершин и рёбер многогранника,
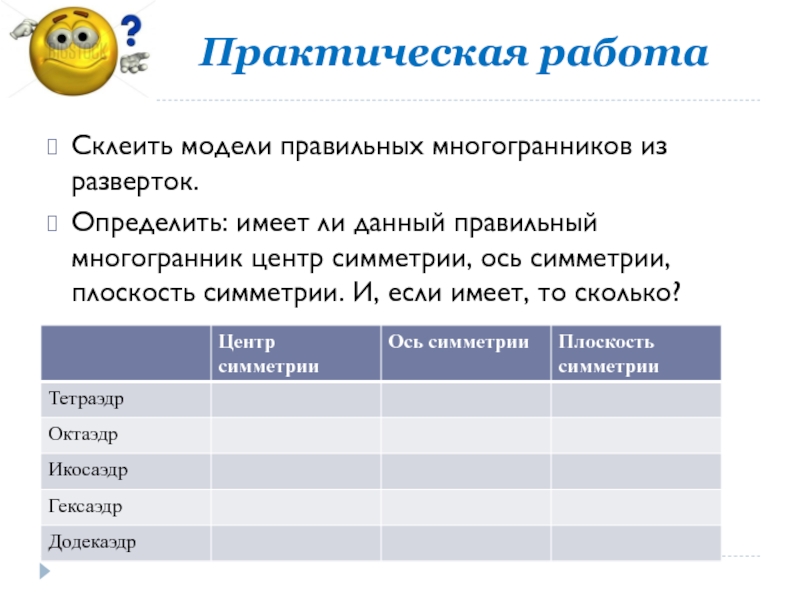
- 33. Практическая работаСклеить модели правильных многогранников из разверток.Определить:
- 34. П. 35-37. № 276-279.Домашнее задание
Слайд 1Симметрия в пространстве. Правильные многогранники
Преподаватель высшей категории, Паневина А.В.
Слайд 3Дайте определение призмы.
Какую призму называют правильной?
Площадь боковой поверхности прямой призмы.
Площадь боковой
Дайте определение пирамиды.
Какую пирамиду называют правильной?
Площадь боковой поверхности правильной пирамиды.
Дайте определение усеченной пирамиды.
Площадь боковой поверхности правильной усеченной пирамиды.
Теория
Слайд 4Математический диктант
Верно ли, что куб является правильной четырехугольной призмой?
Может ли боковая
Могут ли два боковых ребра пирамиды быть перпендикулярны к плоскости основания?
Верно ли, что прямая призма, все боковые грани которой – квадраты, является правильной?
Даны правильная 4-уг. призма, прямоугольный параллелепипед и куб. Определите в каких из этих многогранников ребра могут быть неравными?
Слайд 5Математический диктант
Определите количество сторон многоугольника, лежащего в основании пирамиды, если она
Определите вид четырехугольника, который является сечением правильной треугольной призмы, если это сечение параллельно боковому ребру.
Высота пирамиды проходит через точку пересечения диагоналей параллелограмма, лежащего в основании. Определите вид параллелограмма, если все боковые ребра пирамиды образуют равные углы с плоскостью основания.
Слайд 6«Что может быть больше похоже на мою руку или мое ухо,
Иммануил Кант
Слайд 8Центральная симметрия
Две точки А и А1 называются симметричными относительно точки О,
О - центр симметрии
А
О
А1
Слайд 9Осевая симметрия
Две точки А и А1 называются симметричными относительно прямой а,
а – ось симметрии
А
А1
а
О
Слайд 11Энантиоморфы – это пара зеркально асимметричных объектов (фигур), являющихся зеркальным изображением
Энантиоморфы
Слайд 13 Зеркальная симметрия (ее ещё называют геральдической) использовалась разными народами
Геральдическая симметрия
Слайд 14Двуглавый орел хорошо послужил государству Российскому как символ объединения русских земель
Из истории Российского герба
Слайд 15Изображения на плоскости многих предметов окружающего нас мира имеют ось симметрии:
Симметрия вокруг нас
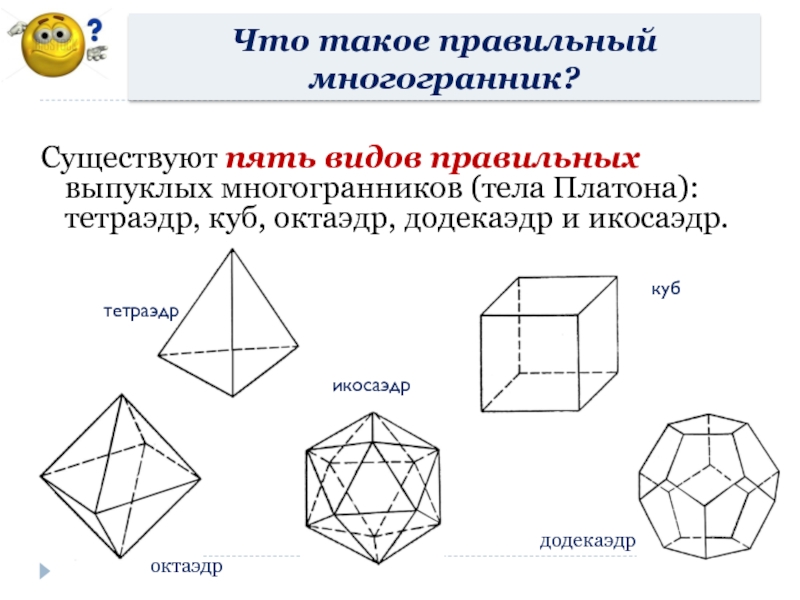
Слайд 19Существуют пять видов правильных выпуклых многогранников (тела Платона): тетраэдр, куб, октаэдр,
Что такое правильный многогранник?
додекаэдр
октаэдр
икосаэдр
куб
тетраэдр
Слайд 20пришли из Древней Греции,
в них указывается число граней:
«эдра»
«тетра» 4;
«гекса» 6;
«окта» 8;
«икоса» 20;
«додека» 12.
Названия многогранников
Слайд 21Что такое правильный многогранник?
Правильных многогранников вызывающе мало, но этот весьма скромный
Л. Кэрролл
Слайд 22 Правильные многогранники иногда называют Платоновыми телами, поскольку
Платон считал, что мир строится из четырёх «стихий» – огня, земли, воздуха и воды, а атомы этих «стихий» имеют форму четырёх правильных многогранников.
Тетраэдр олицетворял огонь, поскольку его вершина устремлена вверх, как у разгоревшегося пламени.
Икосаэдр – как самый обтекаемый – воду.
Куб – самая устойчивая из фигур – землю.
Октаэдр – воздух.
В наше время эту систему можно сравнить с четырьмя состояниями вещества – твёрдым, жидким, газообразным и пламенным.
Пятый многогранник – додекаэдр символизировал весь мир и почитался главнейшим.
Это была одна из первых попыток ввести в науку идею систематизации.
Слайд 23«Космический кубок» Кеплера
Кеплер предположил, что существует связь
Согласно этому предположению, в сферу орбиты Сатурна можно вписать куб, в который вписывается сфера орбиты Юпитера. В неё, в свою очередь, вписывается тетраэдр, описанный около сферы орбиты Марса. В сферу орбиты Марса вписывается додекаэдр, к который вписывается сфера орбиты Земли. А она описана около икосаэдра, в который вписана сфера орбиты Венеры. Сфера этой планеты описана около октаэдра, в который вписывается сфера Меркурия.
Такая модель Солнечной системы получила название «Космического кубка» Кеплера. Результаты своих вычислений учёный опубликовал в книге «Тайна мироздания». Он считал, что тайна Вселенной раскрыта.
Год за годом учёный уточнял свои наблюдения, перепроверял данные коллег, но, наконец, нашёл в себе силы отказаться от заманчивой гипотезы. Однако её следы просматриваются в третьем законе Кеплера, где говориться о кубах средних расстояний от Солнца.
Модель Солнечной
системы И. Кеплера
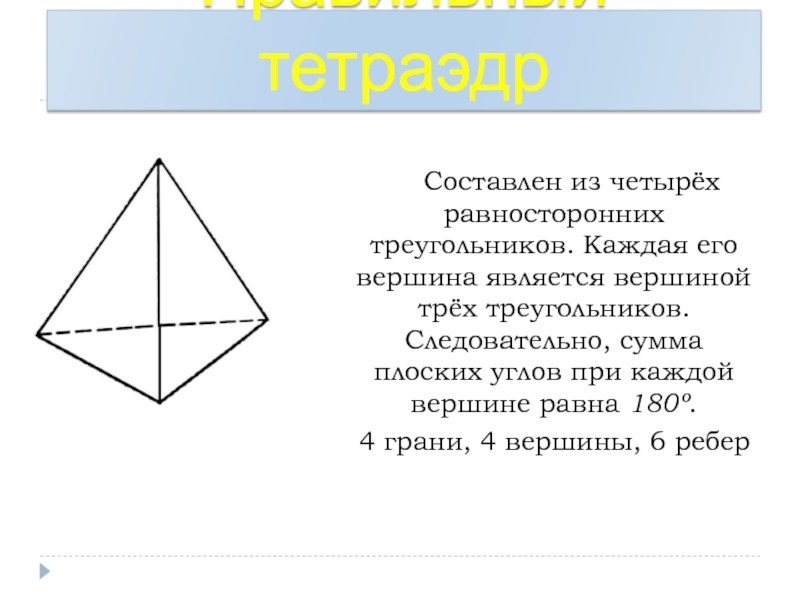
Слайд 24Правильный тетраэдр
Составлен из четырёх равносторонних треугольников. Каждая его вершина
4 грани, 4 вершины, 6 ребер
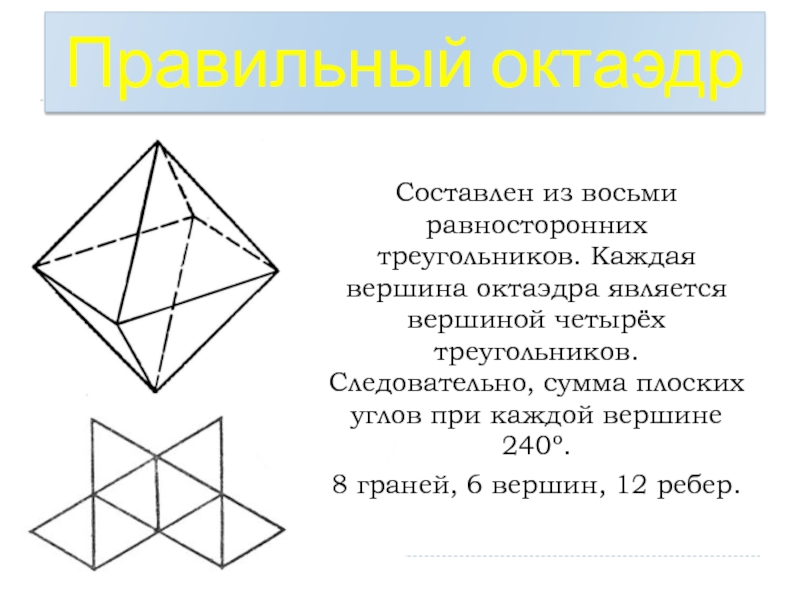
Слайд 26Правильный октаэдр
Составлен из восьми равносторонних треугольников. Каждая вершина октаэдра является вершиной
8 граней, 6 вершин, 12 ребер.
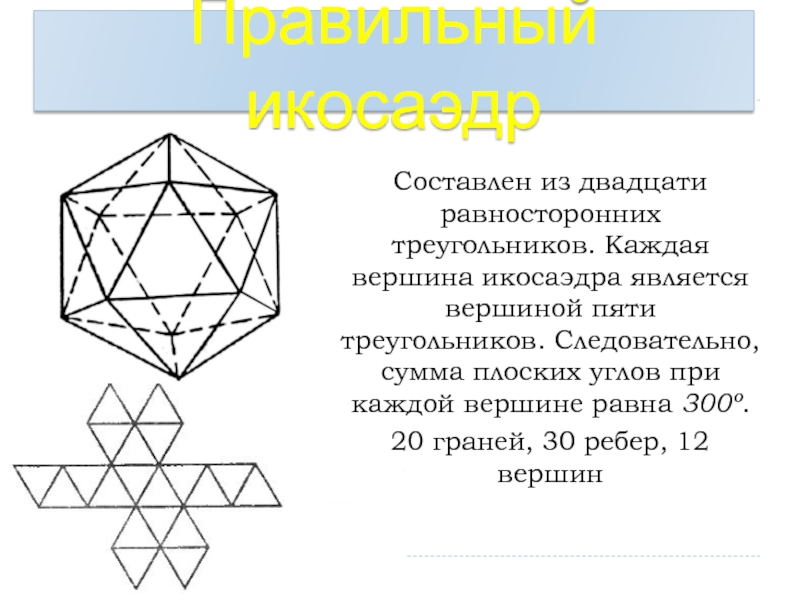
Слайд 27Правильный икосаэдр
Составлен из двадцати равносторонних треугольников. Каждая вершина икосаэдра является вершиной
20 граней, 30 ребер, 12 вершин
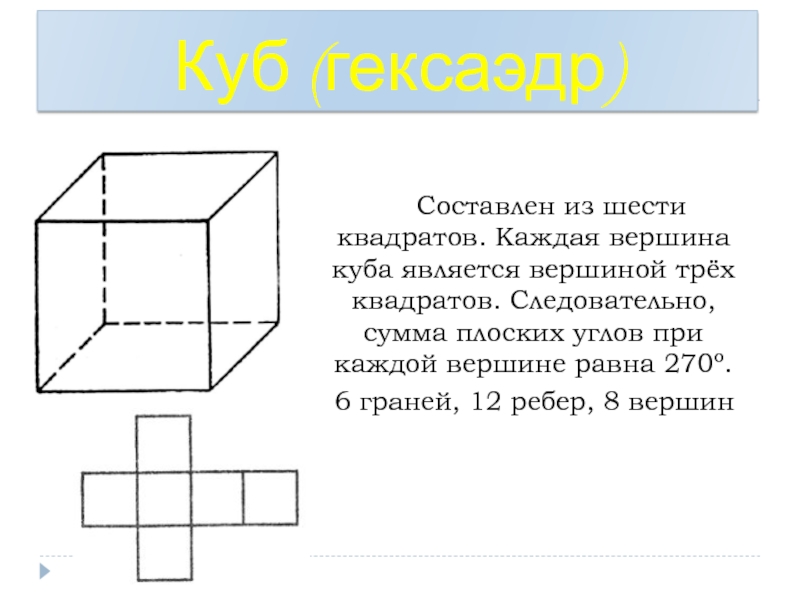
Слайд 28 Составлен из шести квадратов. Каждая вершина куба является вершиной
6 граней, 12 ребер, 8 вершин
Куб (гексаэдр)
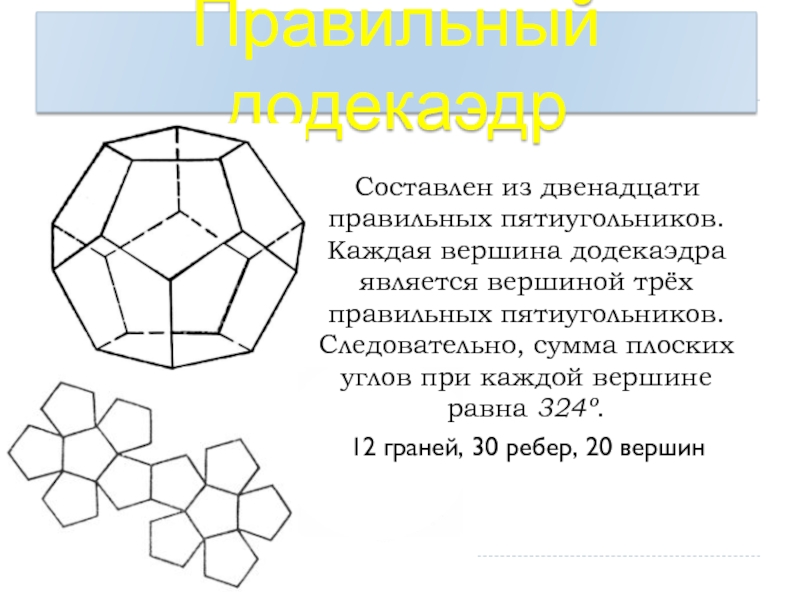
Слайд 30Правильный додекаэдр
Составлен из двенадцати правильных пятиугольников. Каждая вершина додекаэдра является
12 граней, 30 ребер, 20 вершин
Слайд 31Правильного многогранника, гранями которого являются правильные шестиугольники, семиугольники и вообще n-угольники,
Формула Эйлера
Сумма числа граней и вершин любого многогранника равна числу рёбер, увеличенному на 2.
Г + В = Р + 2
Число граней плюс число вершин минус число рёбер в любом многограннике равно 2.
Г + В Р = 2
Правильные многогранники
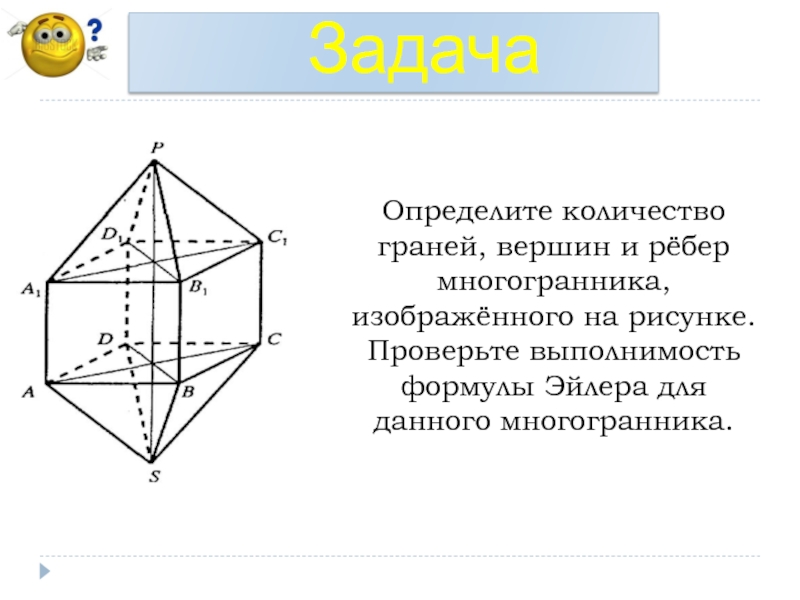
Слайд 32Определите количество граней, вершин и рёбер многогранника, изображённого на рисунке. Проверьте
Задача