Геометрия Лобачевского
- Главная
- Разное
- Образование
- Спорт
- Естествознание
- Природоведение
- Религиоведение
- Французский язык
- Черчение
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, фоны, картинки для презентаций
- Экология
- Экономика
Презентация, доклад к поисковой работе Дудина Ивана Геометрия Лобачевского
Содержание
- 1. Презентация к поисковой работе Дудина Ивана Геометрия Лобачевского
- 2. Выполнил : Дудин Иван, ученик 7
- 3. Муниципальное общеобразовательное бюджетное учреждение основная общеобразовательная школа № 15 п. ИзыканПоисково – исследовательская работаГеометрия Лобачевского
- 4. Познакомиться с геометрией Лобачевского;Провести эксперимент «Иллюзии зрения»;Выяснить
- 5. Пространство вокруг все, что нас окружает,Уметь чтоб
- 6. Евклид (III век до н. э.) Древнегреческий
- 7. …«Начала» Евклида – отчета начало, Основой всех
- 8. Видите движение на этой картинке?Эксперимент «Иллюзии зрения»
- 9. На рисунке буквы расположены параллельно (стоят прямо) или нет?На рисунке изображена спираль или несколькоокружностей?
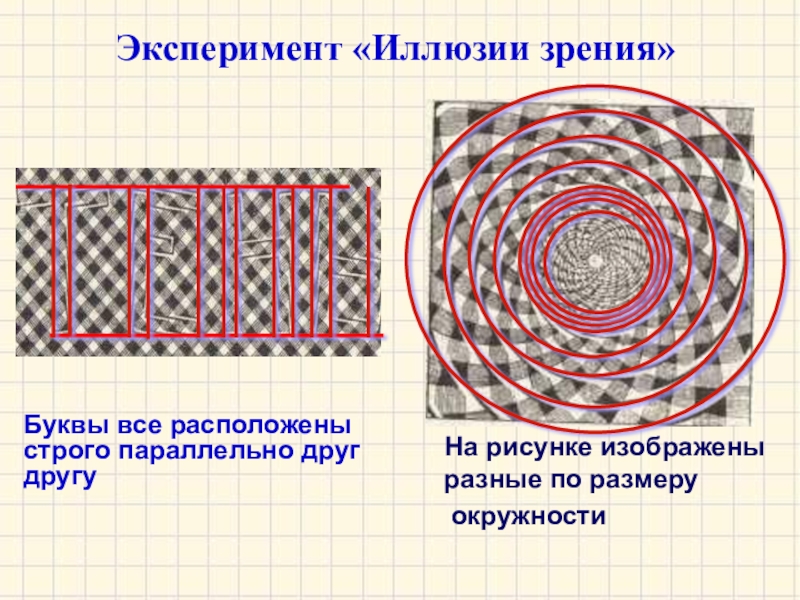
- 10. Эксперимент «Иллюзии зрения»Буквы все расположены строго параллельно
- 11. Итоги эксперимента «Иллюзии зрения»
- 12. Все! Перечеркнуты “Начала”. Довольно мысль на
- 13. Евклид (III век до н. э.) Древнегреческий
- 14. Евклидова аксиома о параллельных:через точку, не
- 15. Николай Иванович Лобачевский
- 16. ВЫВОД: Заменив
- 17. Был мудрым Евклид, Но его параллели,Как будто
- 18. Слайд 18
- 19. В реальном трехмерном пространстве геометрия
- 20. Риманова геометрия, многомерное обобщение геометрии на
- 21. Слайд 21
- 22. Феликс Христиан Клейн
- 23. Бутылка Клейна В 1882г немецкий математик
- 24. Альберт ЭйнштейнМиф четвертый
- 25. Применение геометрии Лобачевского в реальном миреГеометрия
- 26. Создатели неевклидовой геометрии Януш
- 27. Карл Фридрих Гаусс
- 28. Несмотря на все кажущиеся странности,
- 29. Благодарю за внимание!!!
Выполнил : Дудин Иван, ученик 7 класса МОБУ ООШ № 15Руководитель: Беда Ольга Васильевнаучитель математики МОБУ ООШ № 15
Слайд 1Муниципальное общеобразовательное бюджетное учреждение основная общеобразовательная школа № 15 п. Изыкан
Поисково
– исследовательская работа
Слайд 2
Выполнил : Дудин Иван, ученик
7 класса
МОБУ ООШ №
15
Руководитель: Беда Ольга Васильевна
учитель математики
МОБУ ООШ № 15
Слайд 3Муниципальное общеобразовательное бюджетное учреждение основная общеобразовательная школа № 15 п. Изыкан
Поисково
– исследовательская работа
Геометрия Лобачевского
Слайд 4Познакомиться с геометрией Лобачевского;
Провести эксперимент «Иллюзии зрения»;
Выяснить отличия геометрии Евклида от
геометрии Лобачевского;
Рассмотреть мифы о геометрии Лобачевского;
Узнать существуют ли, кроме геометрии Лобачевского ещё неевклидовы геометрии, кто их автор и особенности;
Найти применение неевклидовых геометрий.
Рассмотреть мифы о геометрии Лобачевского;
Узнать существуют ли, кроме геометрии Лобачевского ещё неевклидовы геометрии, кто их автор и особенности;
Найти применение неевклидовых геометрий.
Цели :
Слайд 5Пространство вокруг все, что нас окружает,
Уметь чтоб легко описать без труда,
Учитель
нам в школе один помогает,
Без этой науки совсем никуда!
Её геометрией древние греки
Назвали в далёкие древние годы,
Они измеряли и земли, и реки,
Ища в их течениях тихие броды…
Без этой науки совсем никуда!
Её геометрией древние греки
Назвали в далёкие древние годы,
Они измеряли и земли, и реки,
Ища в их течениях тихие броды…
Слайд 6Евклид (III век до н. э.) Древнегреческий математик, автор первого трактата по
геометрии «Начала» (в 13 книгах).
Слайд 7…«Начала» Евклида – отчета начало, Основой всех знаний считается в ней, Две тысячи
лет с той поры миновало,
Собой геометрия стала сложней,
Она развивалась как все в этом мире,
И знаний глубоких все больше несла,
Законы в ней, формулы люди открыли,
О ней написав аксиом без числа…
Слайд 9
На рисунке буквы расположены параллельно (стоят прямо) или нет?
На рисунке
изображена спираль или несколько
окружностей?
окружностей?
Слайд 10Эксперимент «Иллюзии зрения»
Буквы все расположены строго параллельно друг другу
На рисунке изображены разные по размеру
окружности
Слайд 12
Все! Перечеркнуты “Начала”.
Довольно мысль на них скучала,
Хоть прав
почти во всем Евклид,
Но быть не вечно постоянству:
И плоскость свернута в пространство,
И мир
Иной имеет вид...
Но быть не вечно постоянству:
И плоскость свернута в пространство,
И мир
Иной имеет вид...
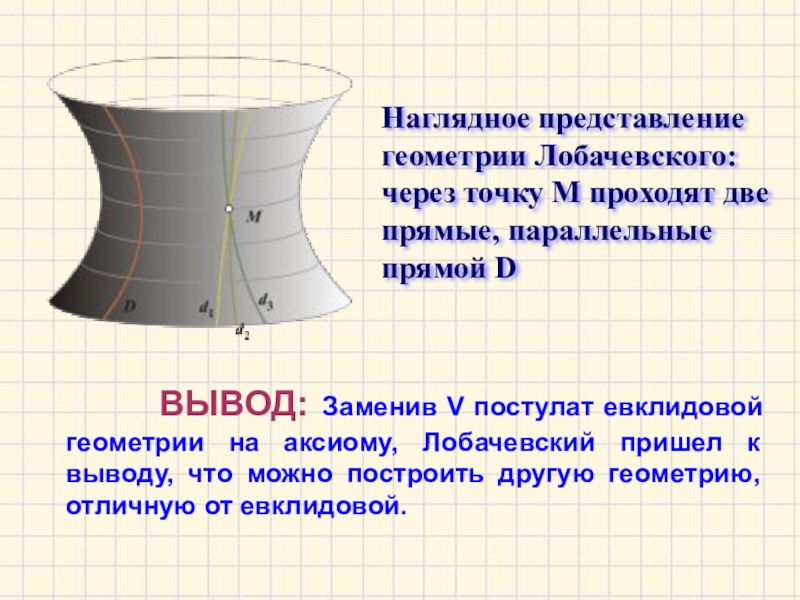
ВЫВОД: Заменив V постулат евклидовой геометрии на аксиому, Лобачевский пришел к выводу, что можно построить другую геометрию, отличную от евклидовой.
Слайд 13Евклид (III век до н. э.) Древнегреческий математик, автор первого трактата по
геометрии «Начала» (в 13 книгах).
В основе всей геометрии греческого математика ЕвклидаВ основе всей геометрии греческого математика Евклида В основе всей геометрии греческого математика Евклида лежало несколько простых первоначальных утверждений (аксиом), которые принимались за истинные без доказательств. Из аксиом путем доказательств выводились более сложные утверждения, из тех выводились еще более сложные.
Слайд 14
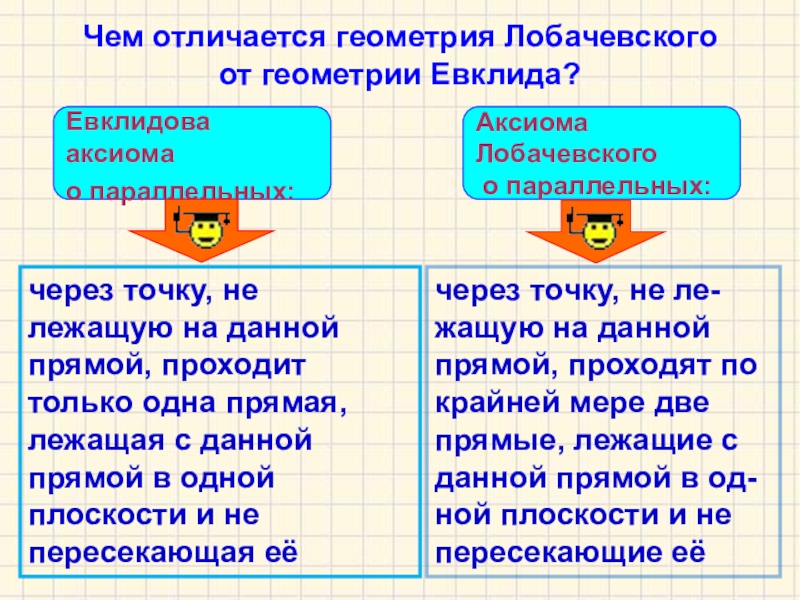
Евклидова аксиома
о параллельных:
через точку, не лежащую на данной прямой,
проходит только одна прямая, лежащая с данной прямой в одной плоскости и не пересекающая её
Аксиома
Лобачевского
о параллельных:
через точку, не ле-жащую на данной прямой, проходят по крайней мере две прямые, лежащие с данной прямой в од-ной плоскости и не пересекающие её
Чем отличается геометрия Лобачевского
от геометрии Евклида?
Слайд 15 Николай Иванович
Лобачевский
1792
- 1856
НАИБОЛЕЕ ПОЛНО РАЗРАБОТАЛ
НЕЕВКЛИДОВУ ГЕОМЕТРИЮ.
ЗАСЛУГОЙ ЛОБАЧЕВСКОГО , КАК
УЧЕНОГО , ЯВЛЯЕТСЯ ТО, ЧТО
ОН ВПЕРВЫЕ ПРОБИЛ БРЕШЬ В
ВОСПРИЯТИИ ГЕОМЕТРИИ КАК
ЕДИНСТВЕННО МЫСЛИМОЙ
ЛОГИЧЕСКОЙ СИСТЕМЫ.
НАИБОЛЕЕ ПОЛНО РАЗРАБОТАЛ
НЕЕВКЛИДОВУ ГЕОМЕТРИЮ.
ЗАСЛУГОЙ ЛОБАЧЕВСКОГО , КАК
УЧЕНОГО , ЯВЛЯЕТСЯ ТО, ЧТО
ОН ВПЕРВЫЕ ПРОБИЛ БРЕШЬ В
ВОСПРИЯТИИ ГЕОМЕТРИИ КАК
ЕДИНСТВЕННО МЫСЛИМОЙ
ЛОГИЧЕСКОЙ СИСТЕМЫ.
Слайд 16 ВЫВОД: Заменив V постулат евклидовой геометрии
на аксиому, Лобачевский пришел к выводу, что можно построить другую геометрию, отличную от евклидовой.
Наглядное представление геометрии Лобачевского: через точку M проходят две прямые, параллельные прямой D
Слайд 17Был мудрым Евклид,
Но его параллели,
Как будто бы вечные сваи легли.
И мысли его, что как стрелы летели,
Всегда оставались в пределах Земли.
А там, во вселенной, другие законы,
Там точками служат иные тела.
И там параллельных лучей миллионы
Природа сквозь Марс, может быть, провела
Слайд 18
…Чем Коперник был для Птолемея,
тем был Лобачевский для Евклида…
В. Клиффорд
Геометрия Лобачевского -геометрическая теория, основанная на тех же основных посылках, что и обычная евклидова геометрия, за исключением аксиомы о параллельных, которая заменяется на аксиому о параллельных Лобачевского
Миф первый
Слайд 19
В реальном трехмерном пространстве геометрия Лобачевского реализуется частично
на поверхностях отрицательной кривизны, например, на псевдосфере.
Миф второй
Слайд 20
Риманова геометрия, многомерное обобщение геометрии на поверхности, представляющее собой теорию
римановых пространств, т. е. таких пространств, где в малых областях приближённо имеет место евклидова геометрия (с точностью до малых высшего порядка сравнительно с размерами области). Риманова геометрия получила своё название по имени Б. Римана, который заложил её основы в 1854.
Миф третий
Слайд 23Бутылка Клейна
В 1882г немецкий математик Феликс Христиан Клейн создал
модель плоскости Лобачевского под названием бутылка Клейна
В отличие от обыкновенной бутылки у этого объекта нет «края», где бы поверхность резко заканчивалась. В отличие от воздушного шара можно пройти путь изнутри наружу, не пересекая поверхность (то есть на самом деле у этого объекта нет «внутри» и нет «снаружи»).
Слайд 25
Применение геометрии
Лобачевского в реальном мире
Геометрия Евклида является частным случаем
геометрии Лобачевского. Наш мир – не мир Евклида, как принято считать? Почему же мы не замечаем разницы?
Как пример можно привести тот факт, что видимый звездный свод это ни что иное, как предельная плоскость. Астрономам после признания достижений Лобачевского пришлось пересчитывать все расстояния между звездами – и ошибки достигали 1/6.
Как пример можно привести тот факт, что видимый звездный свод это ни что иное, как предельная плоскость. Астрономам после признания достижений Лобачевского пришлось пересчитывать все расстояния между звездами – и ошибки достигали 1/6.
Слайд 26Создатели неевклидовой геометрии
Януш Больяй
1802 – 1860
УЖЕ К 1825 ГОДУ ПРИШЕЛ
К ОСНОВНЫМ ПОЛОЖЕНИЯМ
НЕЕВКЛИДОВОЙ ГЕОМЕТРИИ.
ОПУБЛИКОВАЛ СВОИ
ИССЛЕДОВАНИЯ В 1832 ГОДУ
В ПРИЛОЖЕНИИ К ПЕРВОМУ
ТОМУ СОЧИНЕНИЙ СВОЕГО
ОТЦА –
ПРОФЕССОРА МАТЕМАТИКИ.
УЖЕ К 1825 ГОДУ ПРИШЕЛ
К ОСНОВНЫМ ПОЛОЖЕНИЯМ
НЕЕВКЛИДОВОЙ ГЕОМЕТРИИ.
ОПУБЛИКОВАЛ СВОИ
ИССЛЕДОВАНИЯ В 1832 ГОДУ
В ПРИЛОЖЕНИИ К ПЕРВОМУ
ТОМУ СОЧИНЕНИЙ СВОЕГО
ОТЦА –
ПРОФЕССОРА МАТЕМАТИКИ.
Миф пятый
Слайд 27
Карл Фридрих Гаусс
1777-1855
ГАУСС НЕ ОПУБЛИКОВАЛ НИ ОДНОЙ РАБОТЫ ПО НЕЕВКЛИДОВОЙ ГЕОМЕТРИИ, НО В ЕГО ДНЕВНИКАХ НАЙДЕНЫ МАТЕРИАЛЫ, КОТОРЫЕ ОБНАРУЖИВАЮТ, ЧТО ОН ПРИШЕЛ К МЫСЛИ О ВОЗМОЖНОСТИ ПОСТРОЕНИЯ НЕЕВКЛИДОВОЙ ГЕОМЕТРИИ .
Создатели неевклидовой
геометрии
Слайд 28 Несмотря на все кажущиеся странности, геометрия Лобачевского является настоящей
геометрией нашего мира, и Евклидова является только её составной частью. Но в пределах ежедневных измерений Евклидова геометрия дает ничтожно малые ошибки, и мы пользуемся именно ею.
Вывод:
