самым могущественным
средством для изощрения наших умственных
способностей и дает нам возможность
правильно мыслить и рассуждать.
Г. Галилей
Подготовил: ученик 9 – В класса КОШ № 41
Научный руководитель: учитель математики
Болотская Л.А.
- Главная
- Разное
- Образование
- Спорт
- Естествознание
- Природоведение
- Религиоведение
- Французский язык
- Черчение
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, фоны, картинки для презентаций
- Экология
- Экономика
Презентация, доклад к научно - исследовательской работе Вневписанная окружность треугольника
Содержание
- 1. Презентация к научно - исследовательской работе Вневписанная окружность треугольника
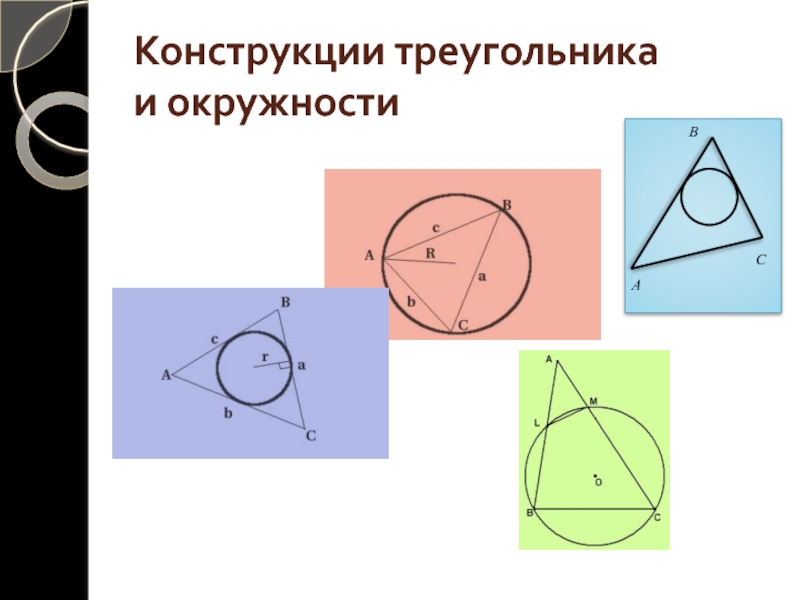
- 2. Конструкции треугольника и окружностиAВ C
- 3. Объект исследования : вневписанная окружность треугольника
- 4. Вневписанная окружность Оа – центр
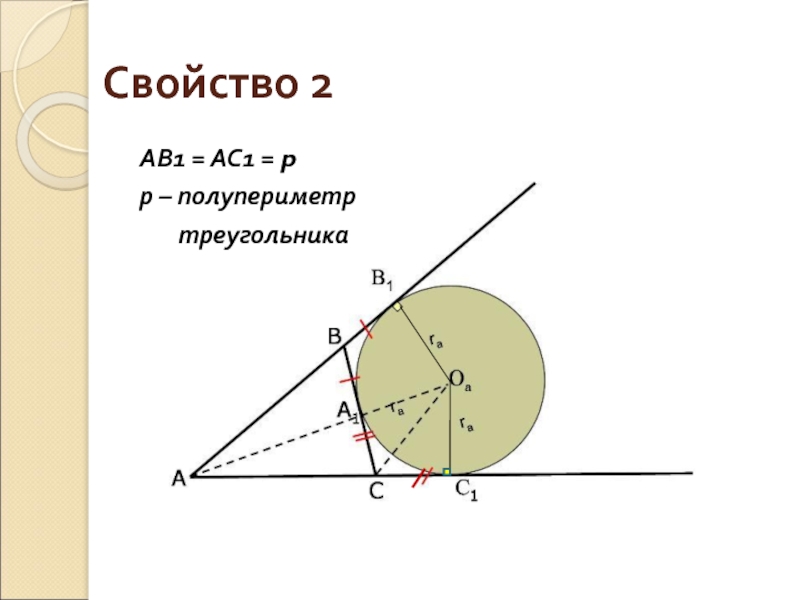
- 5. Свойство 2 АВ1 = АС1 = pр – полупериметр треугольника
- 6. Теорема 1 Радиус вневписанной окружности,
- 7. Теорема 2 Радиус
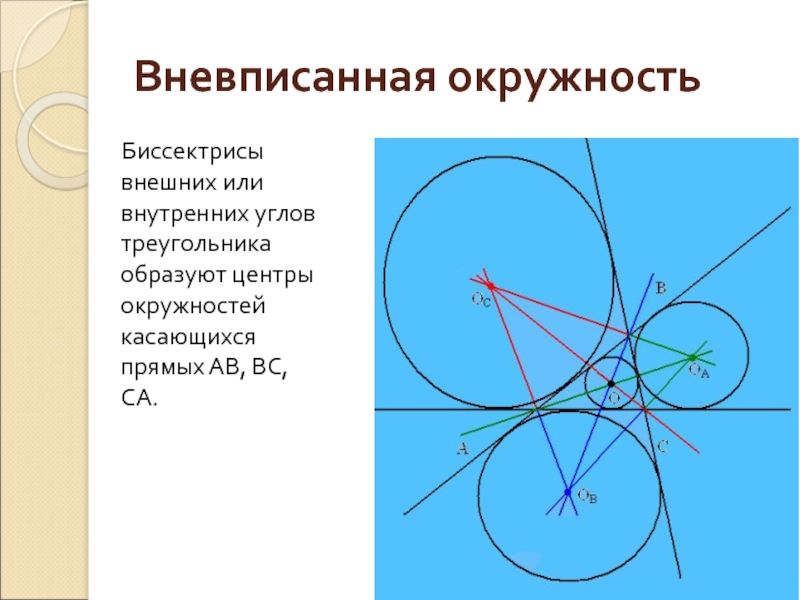
- 8. Вневписанная окружность Биссектрисы внешних или
- 9. Теорема 3 Сумма радиусов вневписанных
- 10. Теорема 4 Сумма величин, обратных радиусам вневписанных окружностей, равна величине, обратной радиусу вписанной окружности
- 11. Теорема 5Сумма всех попарных произведений радиусов вневписанных
- 12. Теорема 6 Произведение всех
- 13. Исследование расстояний между точками касания вписанной и
- 14. Исследование расстояний между точками касания вписанной и
- 15. Исследование расстояний между точками касания вписанной и
- 16. Вневписанная окружностьИнтересно, что
- 17. Спасибо за внимание!
Конструкции треугольника и окружностиAВ C
Слайд 3Объект исследования :
вневписанная окружность треугольника
Предмет исследования :
систематизация свойств вневписанной окружности
для решения задач
Систематизация свойств вневписанной окружности для решения задач
Систематизация свойств вневписанной окружности для решения задач
Слайд 4
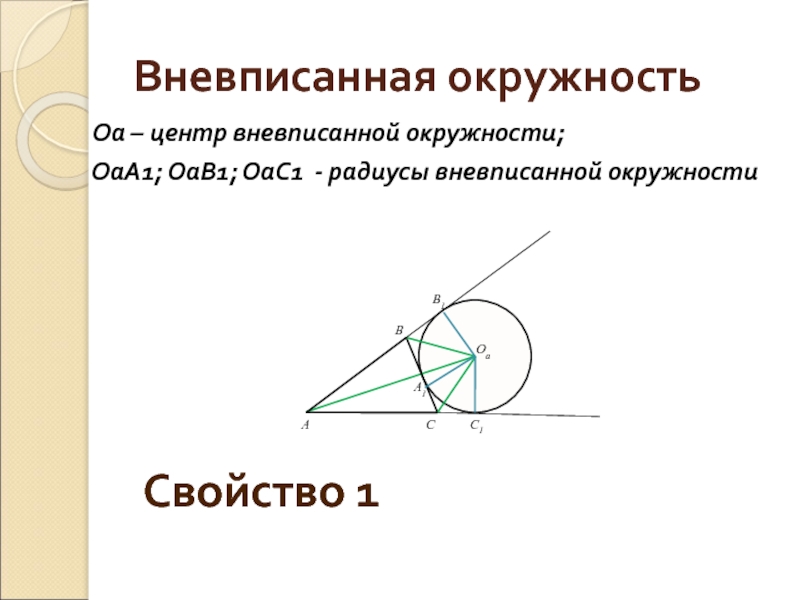
Вневписанная окружность
Оа – центр вневписанной окружности;
ОаА1; ОаВ1; ОаС1 - радиусы вневписанной окружности
В
С1
А
С
Оа
В1
А1
Свойство 1
Слайд 6Теорема 1
Радиус вневписанной окружности, касающейся данной стороны треугольника,
равен отношению площади треугольника к разности полупериметра и этой стороны.
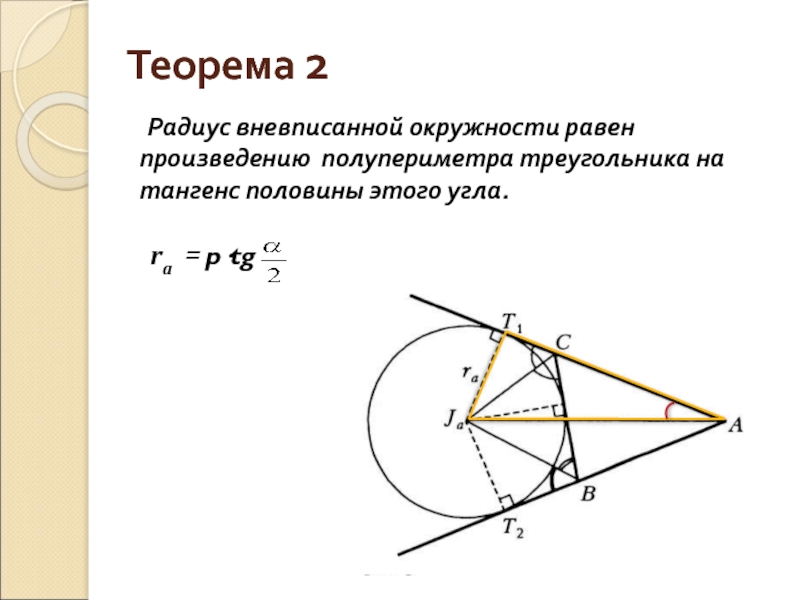
Слайд 7 Теорема 2
Радиус вневписанной окружности равен произведению
полупериметра треугольника на тангенс половины этого угла.
ra = p·tg
ra = p·tg
Слайд 8Вневписанная окружность
Биссектрисы внешних или внутренних углов треугольника образуют
центры окружностей касающихся прямых АВ, ВС, СА.
Слайд 9Теорема 3
Сумма радиусов вневписанных окружностей равна сумме радиуса
вписанной окружности и удвоенного диаметра описанной окружности
ra + rb + rc = r + 4R
ra + rb + rc = r + 4R
Слайд 10Теорема 4
Сумма величин, обратных радиусам вневписанных окружностей, равна величине,
обратной радиусу вписанной окружности
Слайд 11Теорема 5
Сумма всех попарных произведений радиусов вневписанных окружностей равно квадрату полупериметра
треугольника
rarb + rbrc + rcra = p2
rarb + rbrc + rcra = p2
Слайд 12Теорема 6
Произведение всех трех радиусов вневписанных окружностей
равно произведению радиуса вписанной окружности на квадрат полупериметра треугольника
rarbrc = rp2
rarbrc = rp2
Слайд 13Исследование расстояний между точками касания вписанной и вневписанной окружностей со сторонами
треугольника
NK – расстояние между точками касания окружностей к гипотенузе
АN = rc· tg α; АК = .
NK =
A
O
Oc
K
N
r
rc
α
α
C
В
C
Слайд 14Исследование расстояний между точками касания вписанной и вневписанной окружностей со сторонами
треугольника
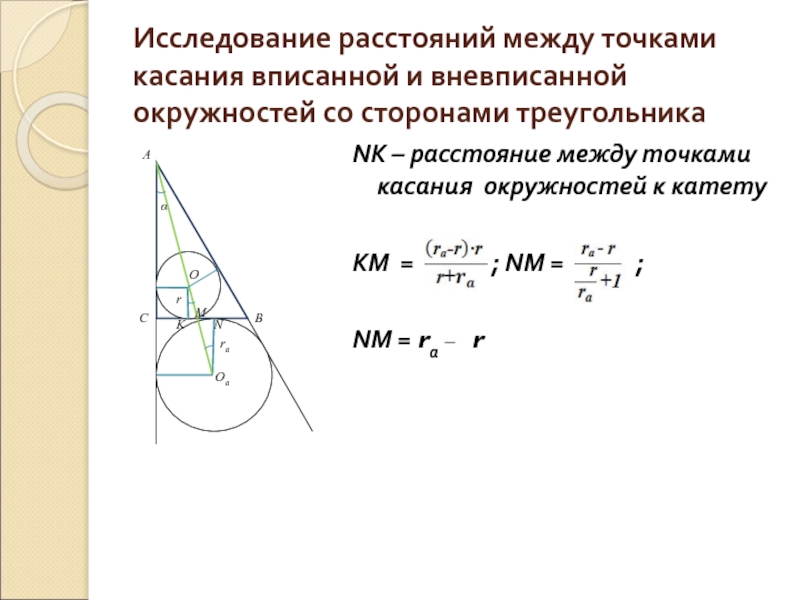
NK – расстояние между точками касания окружностей к катету
КМ = ; NМ = ;
NМ = rа r
A
С
В
N
М
K
r
rа
Оа
O
α
Слайд 15
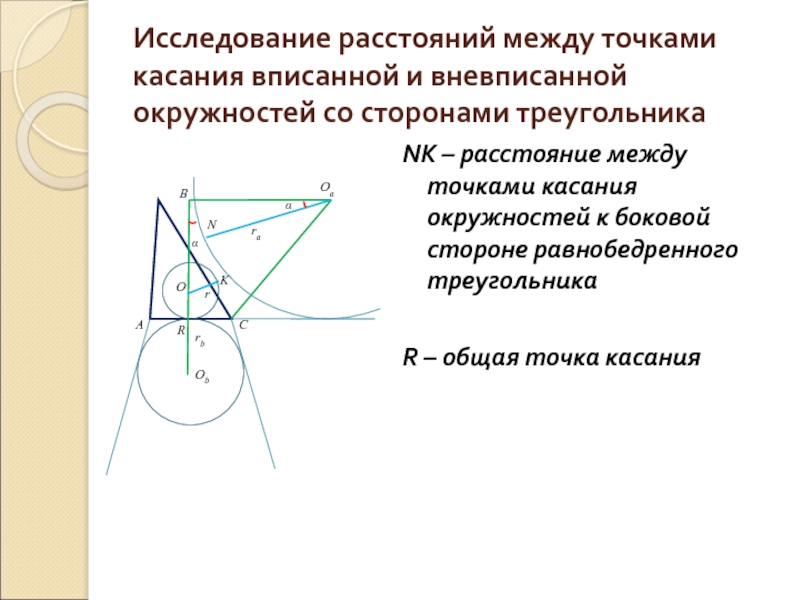
Исследование расстояний между точками касания вписанной и вневписанной окружностей со сторонами
треугольника
NK – расстояние между точками касания окружностей к боковой стороне равнобедренного треугольника
R – общая точка касания
Оb
rb
R
A
B
О
r
C
K
ra
Оа
α
α
N
Слайд 16 Вневписанная окружность
Интересно, что отрезки, соединяющие центр вписанной
в треугольник окружности с центрами вневписанных окружностей, делятся пополам окружностью, описанной вокруг этого треугольника
