СОШ №17 г.Белебея РБ Пьянова Оля, Султанова Софья
Руководитель: учитель математики Лапкарева Е.Г.
- Главная
- Разное
- Образование
- Спорт
- Естествознание
- Природоведение
- Религиоведение
- Французский язык
- Черчение
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, фоны, картинки для презентаций
- Экология
- Экономика
Презентация, доклад к научно-исследовательской работе по математике Оригами в геометрических задачах (7 класс)
Содержание
- 1. Презентация к научно-исследовательской работе по математике Оригами в геометрических задачах (7 класс)
- 2. Цель исследования: найти новые способы решения геометрических
- 3. Гипотеза Многие понятия школьного курса геометрии
- 4. Практическая значимостьЭлектронный учебник «Оригами в геометрии» с
- 5. ОПРОС1. Знаете ли вы, что такое оригами?
- 6. Слайд 6
- 7. Слайд 7
- 8. Слайд 8
- 9. Слайд 9
- 10. Слайд 10
- 11. Слайд 11
- 12. Слайд 12
- 13. Слайд 13
- 14. Слайд 14
- 15. Слайд 15
- 16. Слайд 16
- 17. Слайд 17
- 18. Задача 10. Медиана AM треугольника АВС равна
- 19. «Великий квадрат не имеет пределов» ЯПОНСКАЯ МУДРОСТЬ
Цель исследования: найти новые способы решения геометрических задач и доказательства теорем о свойствах углов в треугольниках с помощью техники оригами.Задача исследования: Познакомиться с историей появления и развития техники оригами;Выяснить среди одноклассников, что они знают об оригами
Слайд 1Научно-исследовательская работа «Оригами в геометрических задачах»
Выполнили : ученики 7 класса МАОУ
Слайд 2Цель исследования: найти новые способы решения геометрических задач и доказательства теорем
о свойствах углов в треугольниках с помощью техники оригами.
Задача исследования:
Познакомиться с историей появления и развития техники оригами;
Выяснить среди одноклассников, что они знают об оригами и где его применяют;
Проанализировать связь оригами и математики на примере решения математических задач и доказательства свойств геометрических фигур;
Исследовать возможность доказательства теорем геометрии с помощью оригами;
Систематизировать собранный материал о применении оригами в геометрии и составить электронный учебник по оригаметрии.
Задача исследования:
Познакомиться с историей появления и развития техники оригами;
Выяснить среди одноклассников, что они знают об оригами и где его применяют;
Проанализировать связь оригами и математики на примере решения математических задач и доказательства свойств геометрических фигур;
Исследовать возможность доказательства теорем геометрии с помощью оригами;
Систематизировать собранный материал о применении оригами в геометрии и составить электронный учебник по оригаметрии.
Попробуй простую фигурку сложить,
И вмиг увлечёт интересное дело.
А. Е. Гайдаенко.
Слайд 3 Гипотеза
Многие понятия школьного курса геометрии просто и наглядно объясняются
демонстрацией оригами. Искусство оригами можно применять для доказательства теорем и для решения задач по геометрии.
Объект исследования: оригами
Предмет исследования: геометрические задачи и теоремы о свойствах углов, медиан, высот и биссектрис в треугольниках.
Методы исследования: сбор и анализ литературы по теме, анализ теорем и геометрических задач в учебниках геометрии; анкетирование одноклассников.
Объект исследования: оригами
Предмет исследования: геометрические задачи и теоремы о свойствах углов, медиан, высот и биссектрис в треугольниках.
Методы исследования: сбор и анализ литературы по теме, анализ теорем и геометрических задач в учебниках геометрии; анкетирование одноклассников.
Слайд 4Практическая значимость
Электронный учебник «Оригами в геометрии» с демонстрацией практических способов решения
геометрических задач можно применять в старших классах на уроках усвоения геометрических понятий, доказательства теорем, на спецкурсах по подготовке к экзаменам. В младших классах информационная часть и видеоматериалы электронного учебника могут стать дидактическим пособием для занятий по развитию мелкой моторики рук, для творческих дел при изготовлении сувениров и подарков к различным праздникам.
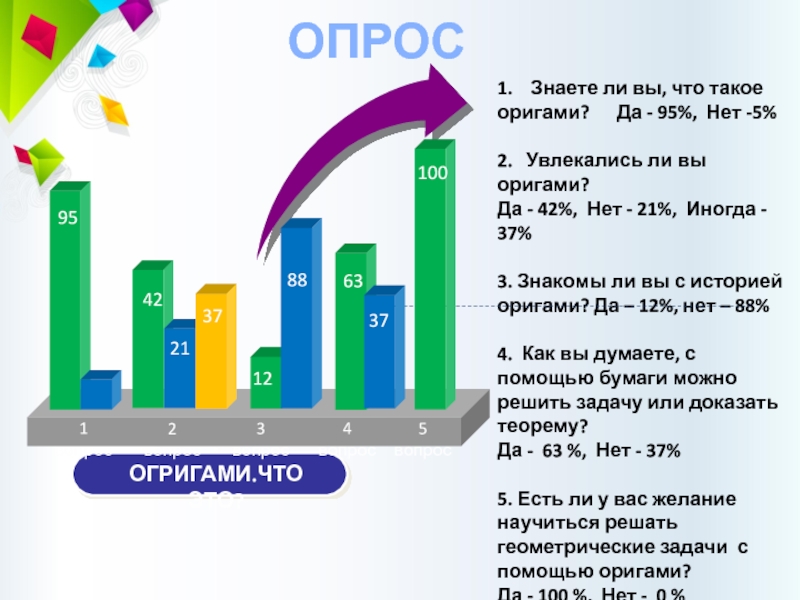
Слайд 5ОПРОС
1. Знаете ли вы, что такое оригами? Да - 95%,
Нет -5%
2. Увлекались ли вы оригами?
Да - 42%, Нет - 21%, Иногда - 37%
3. Знакомы ли вы с историей оригами? Да – 12%, нет – 88%
4. Как вы думаете, с помощью бумаги можно решить задачу или доказать теорему? Да - 63 %, Нет - 37%
5. Есть ли у вас желание научиться решать геометрические задачи с помощью оригами? Да - 100 %, Нет - 0 %
2. Увлекались ли вы оригами?
Да - 42%, Нет - 21%, Иногда - 37%
3. Знакомы ли вы с историей оригами? Да – 12%, нет – 88%
4. Как вы думаете, с помощью бумаги можно решить задачу или доказать теорему? Да - 63 %, Нет - 37%
5. Есть ли у вас желание научиться решать геометрические задачи с помощью оригами? Да - 100 %, Нет - 0 %
ОГРИГАМИ.ЧТО ЭТО?
1 вопрос
2 вопрос
3 вопрос
4 вопрос
95
42
100
12
5 вопрос
21
37
88
37
63
Слайд 18Задача 10. Медиана AM треугольника АВС равна половине стороны BC.
Докажите,
что треугольник АВС прямоугольный. (№231, [1])
Дано: АМ=1/2ВС Доказать: ∆АВС- прямоугольный
Доказательство:
1) Оригамское решение:
1) Найдем середину отрезка ВС и обозначим точкой М, для этого совместим точки В и С.
2) Построим медиану АМ, для этого выполним сгиб через точки А и М.
3) Совместим вершины углов В и С с вершиной угла А (см. Задача 5).
При наложении два угла ےВ и ےС образуют прямой угол , следовательно, ےА=ےВ+ےС=180 °:2=90°(по теореме о сумме углов в треугольнике).Следовательно, ےА =90°и ∆ АВС прямоугольный.
2) Математическое обозначение: АМ=1/2ВС (по условию)=> АМ=ВМ=МС=>∆АВМ и ∆АМС – равнобедренные,
а по свойству углов в равнобедренном треугольнике =>ےВ=ےВАМ и ےС=ےМАС.
По теореме о сумме углов в треугольнике ےА+ےВ+ ےС=180°
ےВАМ + ےМАС= ےА, =>ےВ+ےВАМ +ےС+ےМАС=180 °, а ےВ=ےВАМ и ےС=ےМАС=>2ےВАМ +2ےМАС=180 °
=>ےА=ےВАМ +ےМАС=180 °/2=90 °=>∆АВС-прямоугольный, ч.т.д.
Дано: АМ=1/2ВС Доказать: ∆АВС- прямоугольный
Доказательство:
1) Оригамское решение:
1) Найдем середину отрезка ВС и обозначим точкой М, для этого совместим точки В и С.
2) Построим медиану АМ, для этого выполним сгиб через точки А и М.
3) Совместим вершины углов В и С с вершиной угла А (см. Задача 5).
При наложении два угла ےВ и ےС образуют прямой угол , следовательно, ےА=ےВ+ےС=180 °:2=90°(по теореме о сумме углов в треугольнике).Следовательно, ےА =90°и ∆ АВС прямоугольный.
2) Математическое обозначение: АМ=1/2ВС (по условию)=> АМ=ВМ=МС=>∆АВМ и ∆АМС – равнобедренные,
а по свойству углов в равнобедренном треугольнике =>ےВ=ےВАМ и ےС=ےМАС.
По теореме о сумме углов в треугольнике ےА+ےВ+ ےС=180°
ےВАМ + ےМАС= ےА, =>ےВ+ےВАМ +ےС+ےМАС=180 °, а ےВ=ےВАМ и ےС=ےМАС=>2ےВАМ +2ےМАС=180 °
=>ےА=ےВАМ +ےМАС=180 °/2=90 °=>∆АВС-прямоугольный, ч.т.д.






![Презентация к научно-исследовательской работе по математике Оригами в геометрических задачах (7 класс) Задача 10. Медиана AM треугольника АВС равна половине стороны BC. Докажите, Задача 10. Медиана AM треугольника АВС равна половине стороны BC. Докажите, что треугольник АВС прямоугольный. (№231, [1])Дано:](/img/thumbs/18503ecc917919968928ee80da218eda-800x.jpg)






