- Главная
- Разное
- Образование
- Спорт
- Естествознание
- Природоведение
- Религиоведение
- Французский язык
- Черчение
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, фоны, картинки для презентаций
- Экология
- Экономика
Презентация, доклад интегрированного урока Векторы в физике и математике
Содержание
- 1. Презентация интегрированного урока Векторы в физике и математике
- 2. Векторные величины в математике и физикеЦели:Способствовать формированию
- 3. Векторные величины в математике и физикеИстория развития
- 4. Векторные величины в математике и физикеСравнительный анализ
- 5. Векторные величины в математике и физикеВ математике
- 6. Векторные величины в математике и физикеВиды движения рассматриваемые на уроках
- 7. Векторные величины в математике и физикеГрафик какой функции изображён на рисункелинейнойквадратной обратной пропорциональности
- 8. Векторные величины в математике и физикеЭто график
- 9. Векторные величины в математике и физикеЕсли движение
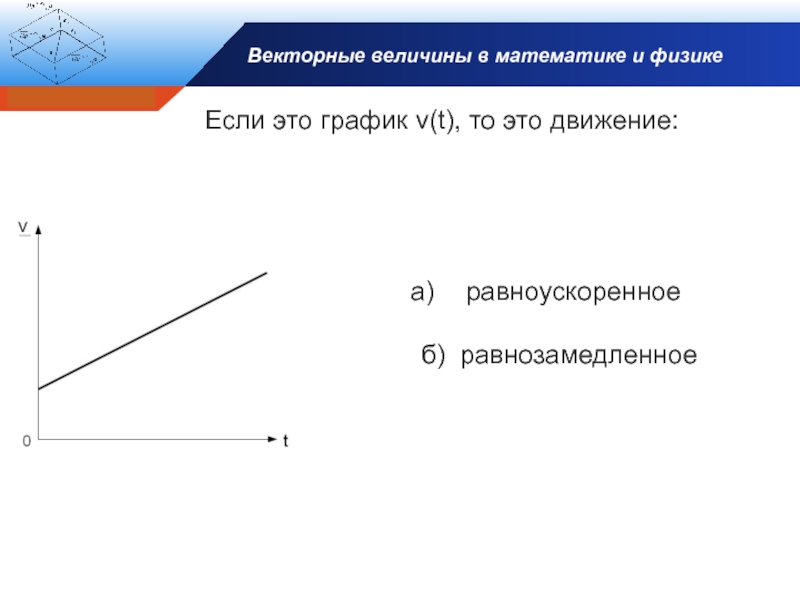
- 10. Векторные величины в математике и физикеЕсли это график v(t), то это движение:равноускоренноеб) равнозамедленноеv
- 11. Векторные величины в математике и физикеДаны уравнения
- 12. Векторные величины в математике и физикеЧто мы
- 13. Векторные величины в математике и физикеНаблюдение за
- 14. Векторные величины в математике и физикеШтурман, определяя
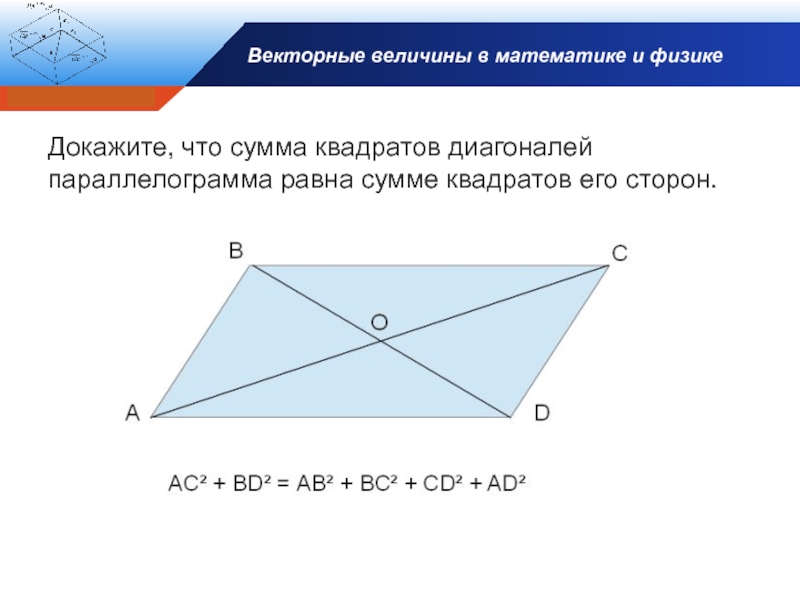
- 15. Векторные величины в математике и физикеДокажите, что сумма квадратов диагоналей параллелограмма равна сумме квадратов его сторон.
- 16. Векторные величины в математике и физикеОпределите величину
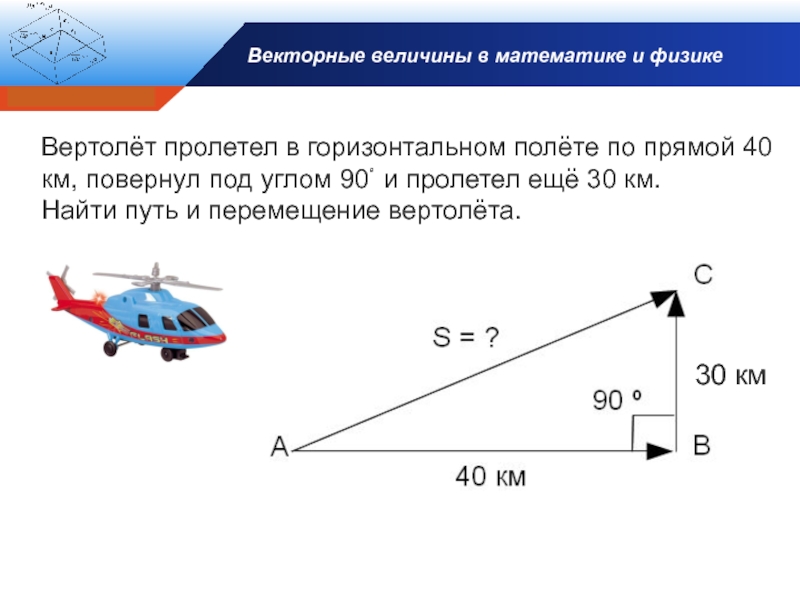
- 17. Векторные величины в математике и физикеВертолёт пролетел
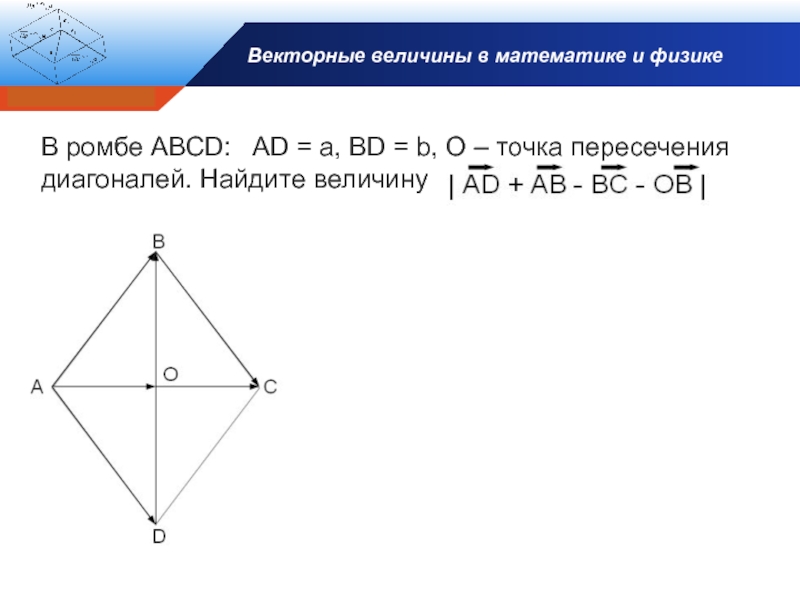
- 18. Векторные величины в математике и физикеВ ромбе
- 19. Векторные величины в математике и физикеДомашнее заданиеОбязательное.
- 20. Векторные величины в математике и физикеПродолжи высказывание:
- 21. СПАСИБО ЗА ВНИМАНИЕ !
Слайд 1Векторные величины в математике и физике
Практика рождается из тесного соединения физики
Ф. Бэкон
Слайд 2Векторные величины в математике и физике
Цели:
Способствовать формированию у учащихся умения применять
Способствовать развитию мыслительных способностей учащихся, памяти, внимания, наблюдательности
Воспитывать устойчивый интерес к изучению математики и физики через реализацию межпредметных связей
Слайд 3Векторные величины в математике и физике
История развития понятия вектора
Возникновение векторного исчисления
Лишь в середине 19 в. усилиями ряда учёных было создано векторное исчисление, в котором операции проводились непосредственно над векторами, без обращения к координатному способу задания.
Основы векторного исчисления были заложены исследованиями английского математика У. Гамильтона и немецкого математика Г. Грассмана по гиперкомплексным числам (1844—50). Их идеи были использованы английским физиком Дж. К. Максвеллом в его работах по электричеству и магнетизму.
Современный вид векторному исчислению придал американский физик Дж. Гиббс. Значительный вклад в развитие векторного исчисления внесли русские учёные. В первую очередь следует отметить работы М. В. Остроградского. Им была доказана основная теорема векторного анализа
Исследования казанского математика А. П. Котельникова по развитию винтового исчисления имели важное значение для механики и геометрии. Эти исследования были продолжены советскими математиками Д. Н. Зейлигером и А. Широковым. Большое влияние на развитие векторного исчисления имела книга «Векторный анализ», написанная в 1907 русским математиком П. О. Сомовым.
Слайд 4Векторные величины в математике и физике
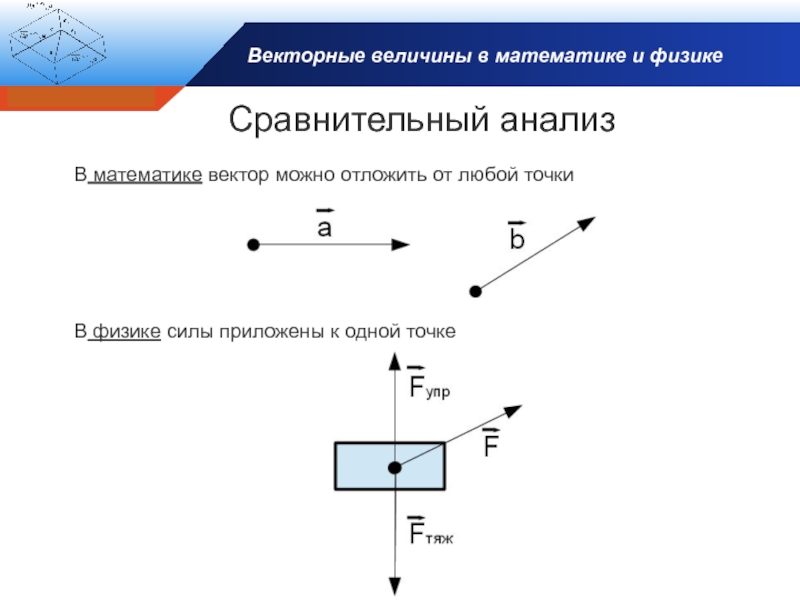
Сравнительный анализ
В математике вектор можно
В физике силы приложены к одной точке
Слайд 5Векторные величины в математике и физике
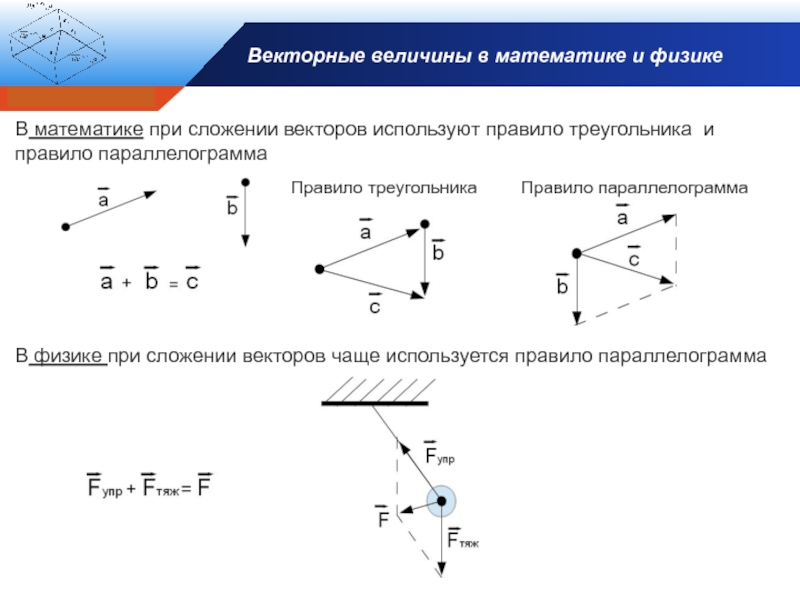
В математике при сложении векторов используют
Правило треугольника
Правило параллелограмма
В физике при сложении векторов чаще используется правило параллелограмма
Слайд 7Векторные величины в математике и физике
График какой функции изображён на рисунке
линейной
квадратной
Слайд 8Векторные величины в математике и физике
Это график функции:
а) возрастающей
б) убывающей
Это
а) у = кх
б) у = кх + b
Слайд 9Векторные величины в математике и физике
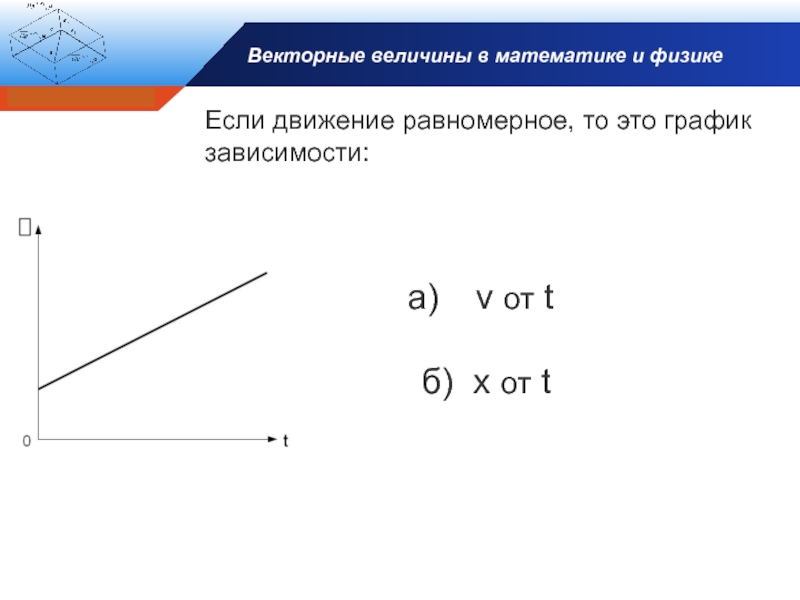
Если движение равномерное, то это график
v от t
б) x от t
Слайд 10Векторные величины в математике и физике
Если это график v(t), то это
равноускоренное
б) равнозамедленное
v
Слайд 11Векторные величины в математике и физике
Даны уравнения :
x = 2 –
x = 2 + 4t
какой это вид движения ?
что общего в движении этих тел ?
чем они отличаются ?
Слайд 12Векторные величины в математике и физике
Что мы оплачиваем при поездке в
Ответ - путь
Слайд 13Векторные величины в математике и физике
Наблюдение за движением футболиста показали: во
Что это за величина – путь или перемещение ?
Ответ - путь
Слайд 14Векторные величины в математике и физике
Штурман, определяя утром положение судна, обнаружил,
Ответ – длина перемещения
Слайд 15Векторные величины в математике и физике
Докажите, что сумма квадратов диагоналей параллелограмма
Слайд 16Векторные величины в математике и физике
Определите величину собственной скорости катера, который,
Слайд 17Векторные величины в математике и физике
Вертолёт пролетел в горизонтальном полёте по
Найти путь и перемещение вертолёта.
30 км
Слайд 18Векторные величины в математике и физике
В ромбе АВСD: AD =
Слайд 19Векторные величины в математике и физике
Домашнее задание
Обязательное.
По сборникам
- СР-1 вариант 2,4 стр. 52-53 на «3»
- СР-1 вариант 6,8 стр. 53-54 на «4»
- СР-1 вариант 1,5 стр. 52-53 на «5»
2. Дополнительное.
Составить задачу по басне Крылова «Лебедь, рак и щука»:
- физическую модель ситуации
- возможно ли, что «воз и ныне там» ?
- рассмотреть в каких ещё литературных произведениях описываются
реальные ситуации, которые можно описать физическими векторными законами. на «4» или «5»
Составить по теме «Векторы» кроссворд или задачу. На «3»
Слайд 20Векторные величины в математике и физике
Продолжи высказывание:
Я знаю как……
построить схему,
выполнить дополнительные построения (достроить до треугольника, параллелограмма и др.
применить математические знания к физическим задачам (формулы, теоремы, определения)
без ошибок выполнить вычисления (свойства действий над числами, таблицей умножения)
какая из форм работы вам больше по душе: в парах, индивидуально, коллективно)