- Главная
- Разное
- Образование
- Спорт
- Естествознание
- Природоведение
- Религиоведение
- Французский язык
- Черчение
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, фоны, картинки для презентаций
- Экология
- Экономика
Презентация, доклад Геометрия 10 класс
Содержание
- 1. Презентация Геометрия 10 класс
- 2. СодержаниеСтереометрия (аксиомы и следствия)Параллельность прямых и плоскостейВзаимное
- 3. ГЕОМЕТРИЯ(ПЛОСКИЙ) (ОБЪЁМНЫЙ)ПЛАНИМЕТРИЯ
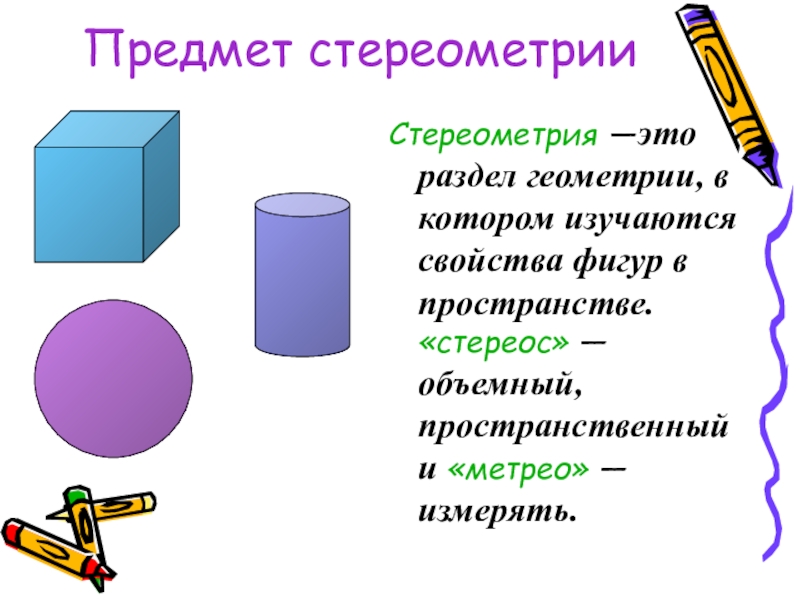
- 4. Предмет стереометрииСтереометрия —это раздел геометрии, в котором
- 5. ОСНОВНЫЕ ФИГУРЫ СТЕРЕОМЕТРИИТОЧКА: А,В,С,…ПРЯМАЯ: а,b,c,d,…; АВ,СР,…ПЛОСКОСТЬ: АВС, MNР,…
- 6. Аксиомы стереометрииАксиома 1:Через любые три точки, не
- 7. Аксиомы стереометрииАксиома 2:Если две точки прямой лежат
- 8. Аксиомы стереометрииАксиома 3:Если две плоскости имеют общую
- 9. Некоторые следствия из аксиомТеорема:Через прямую и
- 10. Некоторые следствия из аксиомТеорема:Через две пересекающиеся прямые проходит плоскость, и притом только одна.MNαba
- 11. Параллельность прямых и плоскостейПараллельность прямых, прямой и плоскости
- 12. Параллельные прямые в пространствеОпределение:Через любую точку
- 13. Параллельность трех прямыхЛемма:Если одна из двух
- 14. Параллельность трех прямыхТеорема:Если две прямые параллельны третьей прямой, то они параллельны.Кabαc
- 15. Параллельность прямой и плоскостиОпределение:Прямая и плоскость называются параллельными, если они не имеют общих точек.αba
- 16. Параллельность прямой и плоскостиТеорема:Если прямая, не лежащая
- 17. Два утверждения, используемые при решениях задач Если
- 18. Два утверждения, используемые при решениях задач2. Если
- 19. Взаимное расположение прямых в пространствеУгол между двумя прямыми
- 20. Скрещивающиеся прямыеОпределение:Две прямые называются скрещивающимися, если они не лежат в одной плоскости.βα
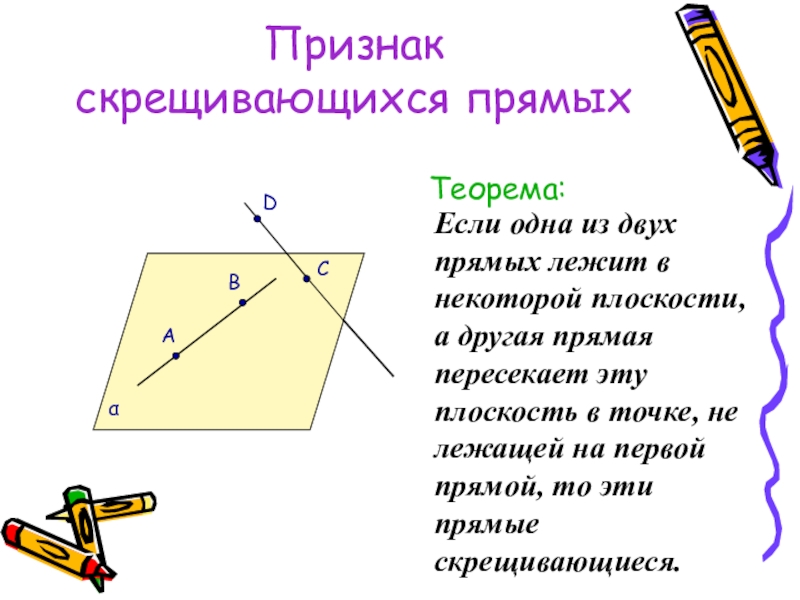
- 21. Признак скрещивающихся прямыхТеорема:Если одна из двух прямых
- 22. Три случая расположения двух прямых в пространствеПрямые
- 23. Теорема о скрещивающихся прямыхТеорема:Через каждую из двух
- 24. Углы с сонаправленными сторонамиТеорема:Если стороны двух углов соответственно сонаправлены, то такие углы равны.O1OAA1BB1
- 25. Параллельность плоскостей
- 26. Параллельные плоскости Две плоскости называются параллельными, если они не пересекаются. Определение:аαββα
- 27. Признак параллельности двух плоскостей Если две пересекающиеся
- 28. Свойства параллельных плоскостей1. Если две параллельные плоскости пересечены третьей, то линий их пересечения параллельны.βαγba
- 29. Свойства параллельных плоскостей2. Отрезки параллельных прямых, заключенные между параллельными плоскостями, равны.βαγBADC
- 30. Перпендикулярность прямых и плоскостей
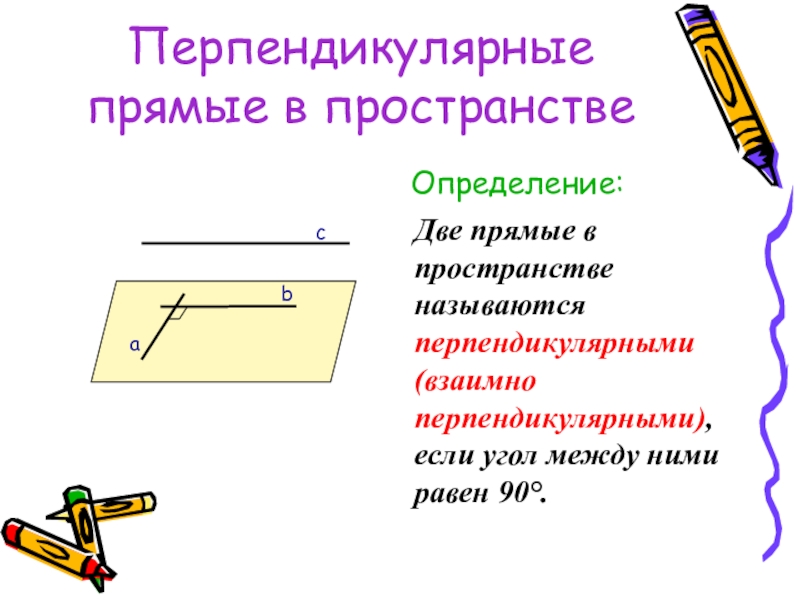
- 31. Перпендикулярные прямые в пространствеОпределение:Две прямые в пространстве
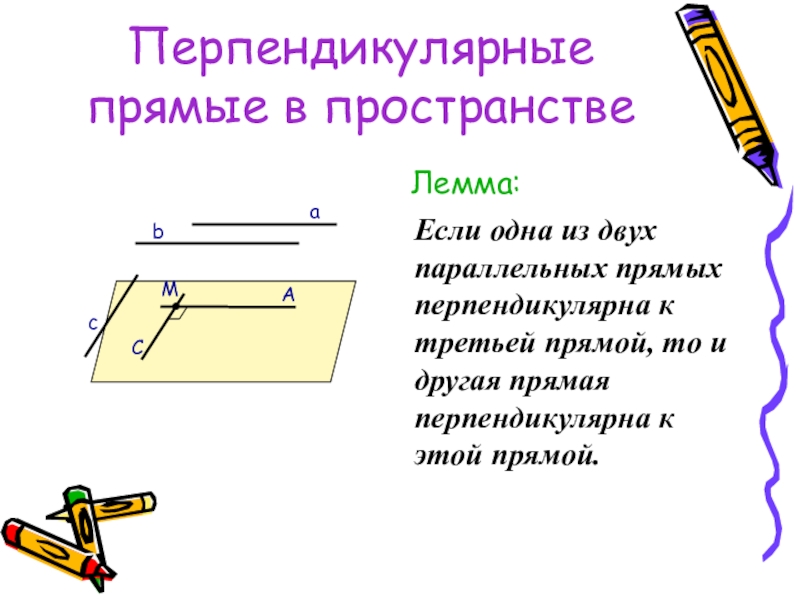
- 32. Перпендикулярные прямые в пространствеЛемма:Если одна из двух
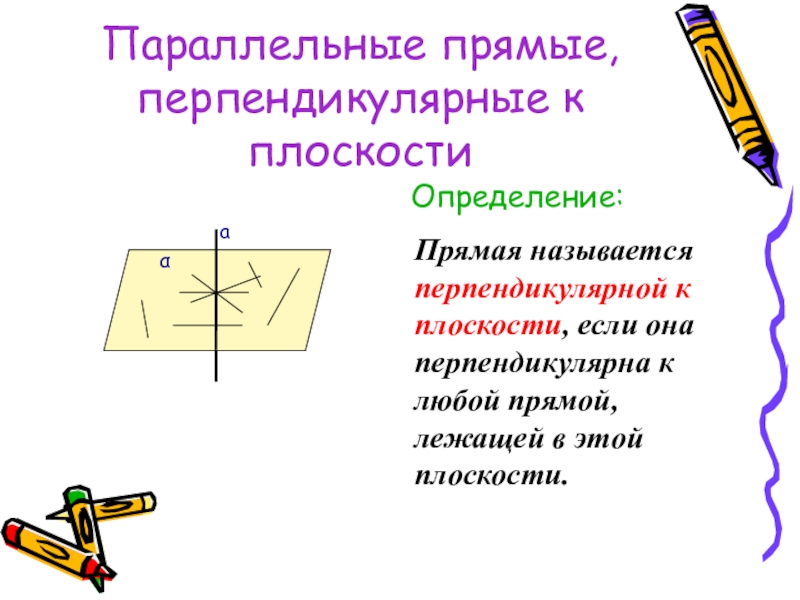
- 33. Параллельные прямые, перпендикулярные к плоскостиОпределение:Прямая называется
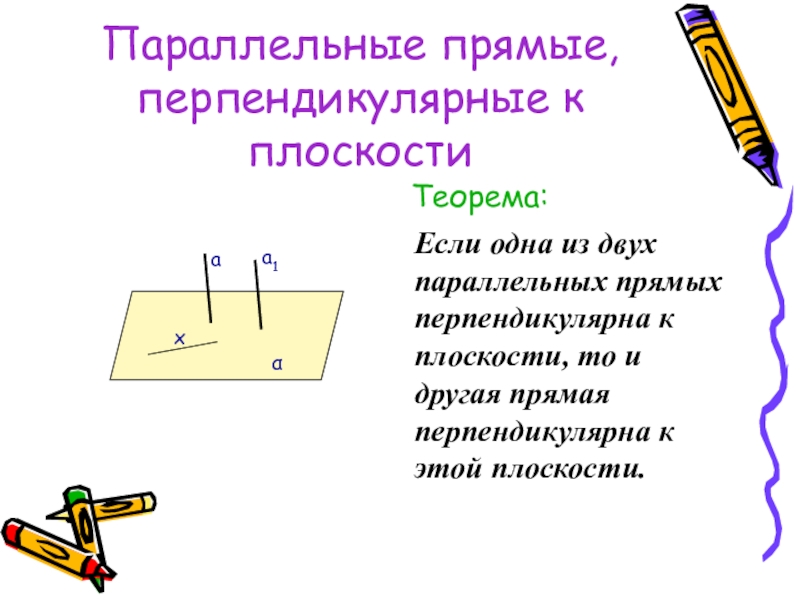
- 34. Параллельные прямые, перпендикулярные к плоскостиТеорема:Если одна
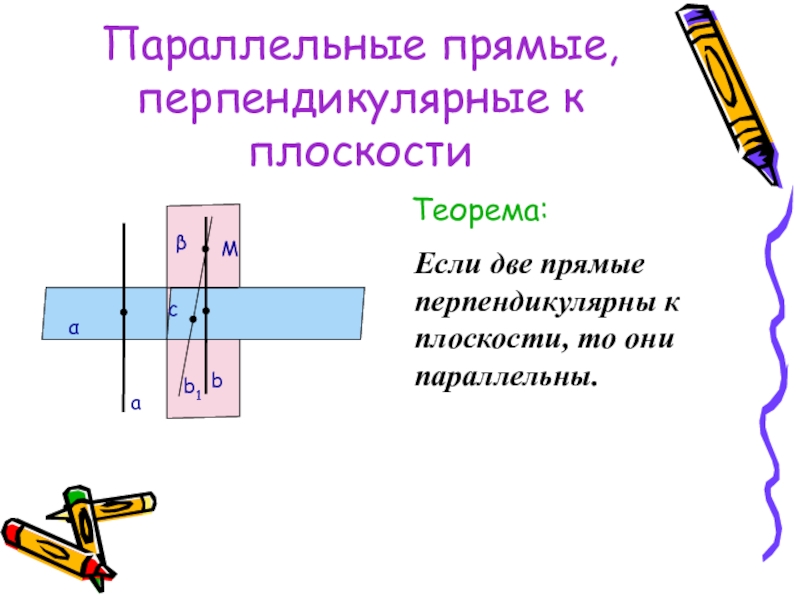
- 35. Параллельные прямые, перпендикулярные к плоскостиТеорема:Если две прямые перпендикулярны к плоскости, то они параллельны.βαMbab1c
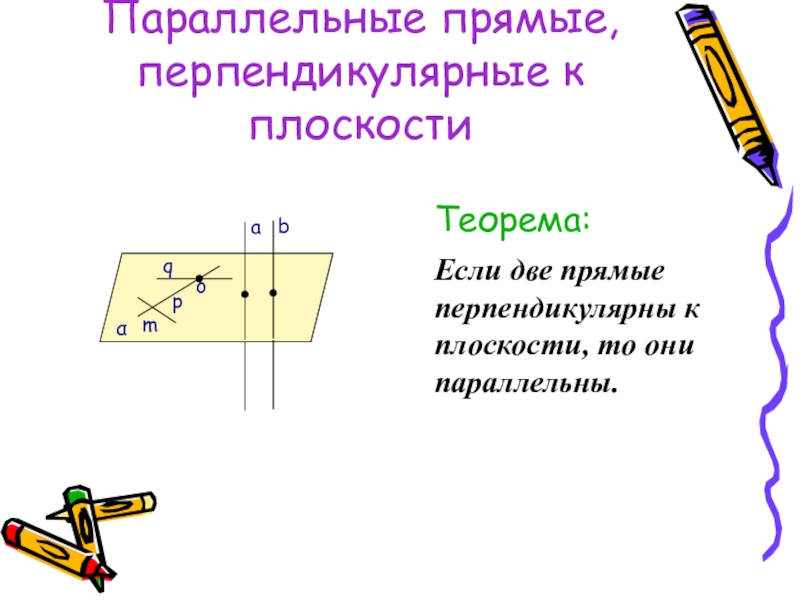
- 36. Параллельные прямые, перпендикулярные к плоскостиТеорема:Если две прямые перпендикулярны к плоскости, то они параллельны.qαmoapb
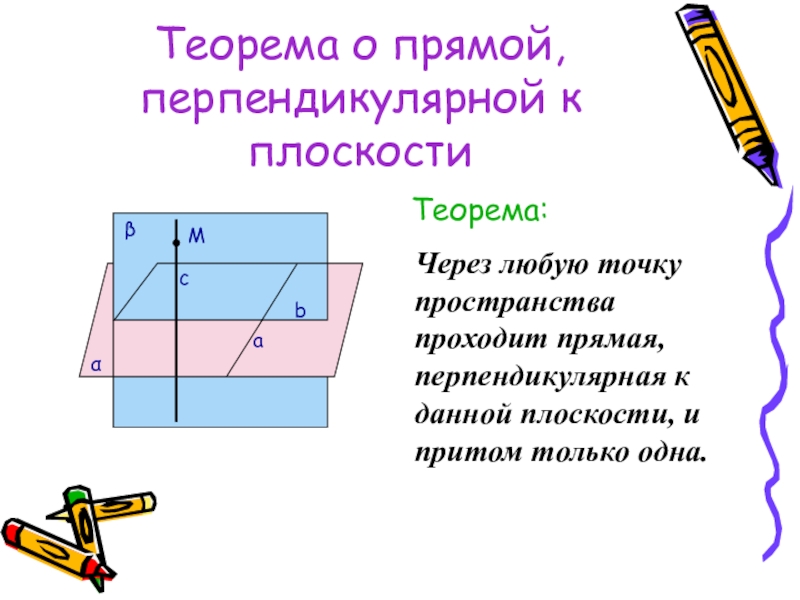
- 37. Теорема о прямой, перпендикулярной к плоскостиТеорема:Через любую
- 38. Перпендикулярные и наклонныеУгол между прямой и плоскостью
- 39. Расстояние от точки до плоскостиОтрезок АН
- 40. Расстояние от точки до плоскостиАМ называется
- 41. Расстояние от точки до плоскостиПерпендикуляр, проведенный
- 42. Замечания1. Расстояние от произвольной точки одной из
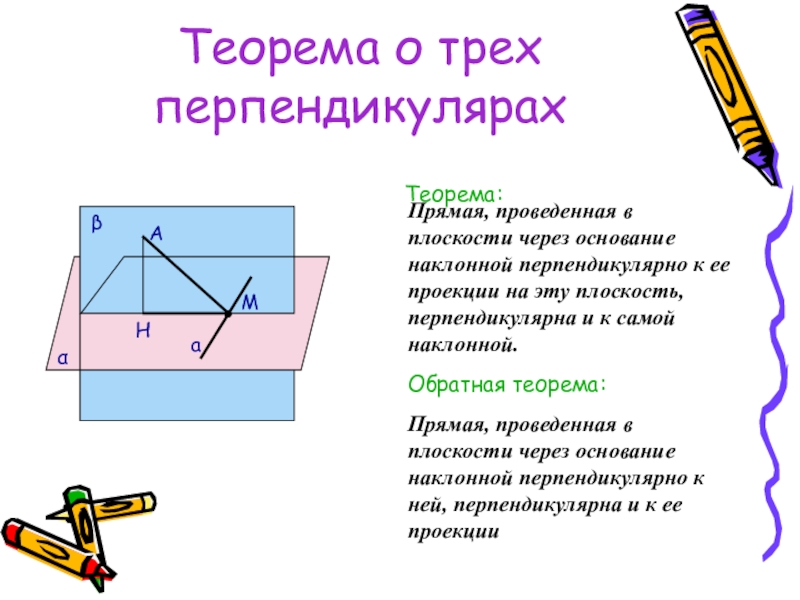
- 43. Теорема о трех перпендикулярахТеорема:Прямая, проведенная в плоскости
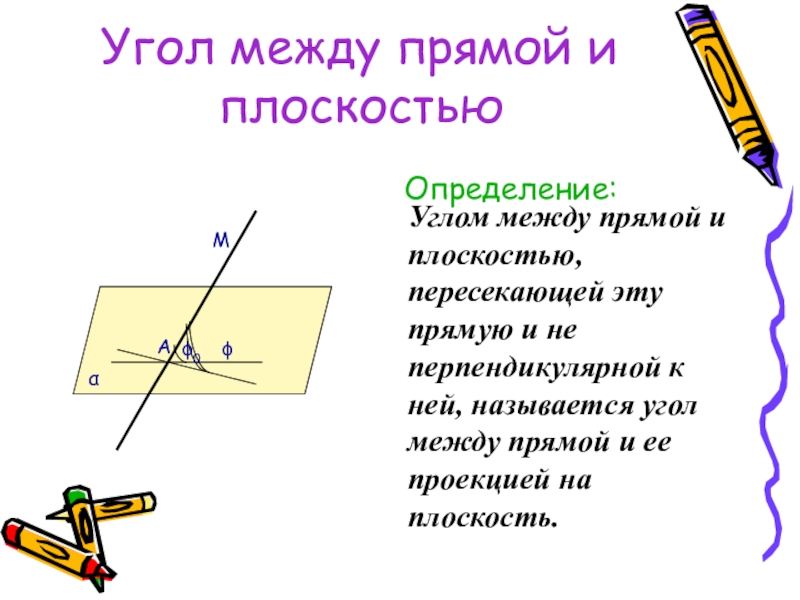
- 44. Угол между прямой и плоскостьюОпределение:Углом между прямой
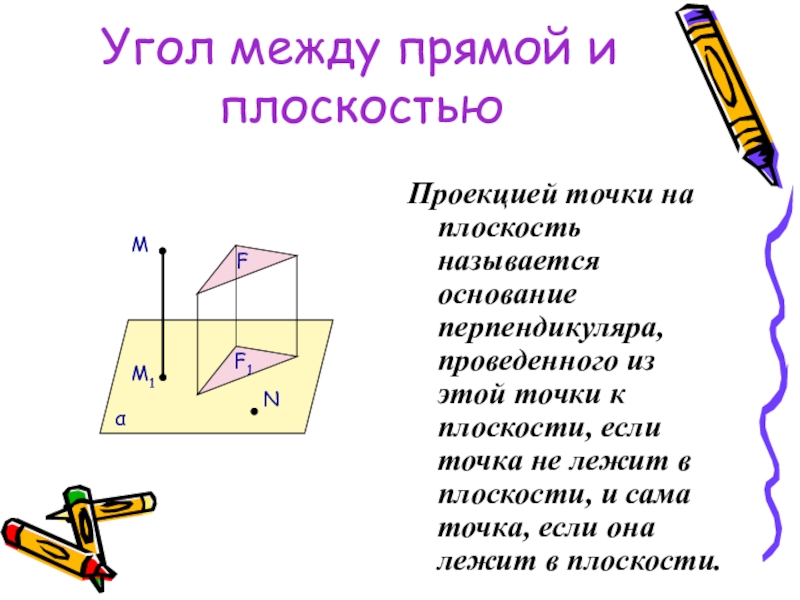
- 45. Угол между прямой и плоскостьюПроекцией точки на
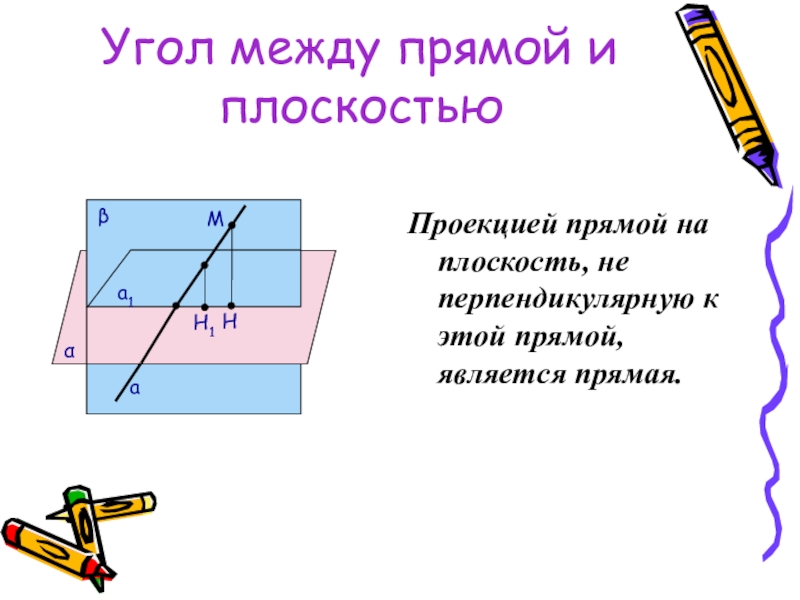
- 46. Угол между прямой и плоскостьюПроекцией прямой на плоскость, не перпендикулярную к этой прямой, является прямая.βαH1aHa1M
- 47. Двугранный уголПерпендикулярность плоскостей
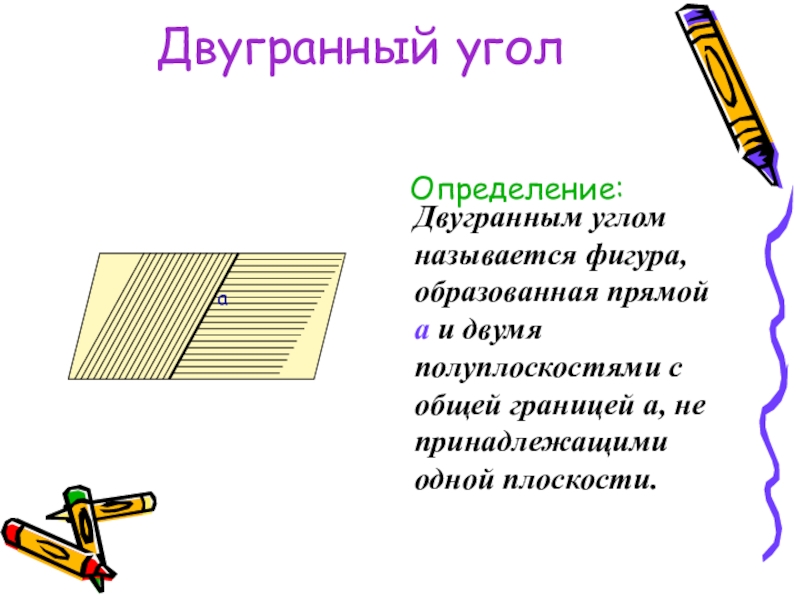
- 48. Двугранный уголОпределение:aДвугранным углом называется фигура, образованная прямой
- 49. Двугранный уголПолуплоскости, образующие двугранный угол, называются его
- 50. Двугранный уголОтметим на ребре двугранного угла какую
- 51. Двугранный уголВсе линейные углы двугранного угла равны
- 52. Виды двугранных угловДвугранный угол называется прямым (острым, тупым), если он равен 90° (меньше 90°, больше 90°).90°45°110°ПрямойТупойОстрый
- 53. Признак перпендикулярности двух плоскостейОпределение:Две пересекающиеся плоскости называются
- 54. Признак перпендикулярности двух плоскостейТеорема:Если одна из двух
- 55. Признак перпендикулярности двух плоскостейСледствие:Плоскость, перпендикулярна к прямой,
СодержаниеСтереометрия (аксиомы и следствия)Параллельность прямых и плоскостейВзаимное расположение прямых в пространствеПараллельность плоскостейПерпендикулярность прямых и плоскостейПерпендикулярные и наклонныеДвугранный угол
Слайд 2Содержание
Стереометрия (аксиомы и следствия)
Параллельность прямых и плоскостей
Взаимное расположение прямых в пространстве
Параллельность
плоскостей
Перпендикулярность прямых и плоскостей
Перпендикулярные и наклонные
Двугранный угол
Перпендикулярность прямых и плоскостей
Перпендикулярные и наклонные
Двугранный угол
Слайд 3ГЕОМЕТРИЯ
(ПЛОСКИЙ) (ОБЪЁМНЫЙ)
ПЛАНИМЕТРИЯ СТЕРЕОМЕТРИЯ
(ТОЧКА, ПРЯМАЯ)
(ТОЧКА, ПРЯМАЯ,
ПЛОСКОСТЬ)
ПЛОСКОСТЬ)
Слайд 4Предмет стереометрии
Стереометрия —это раздел геометрии, в котором изучаются свойства фигур в
пространстве. «стереос» — объемный, пространственный и «метрео» — измерять.
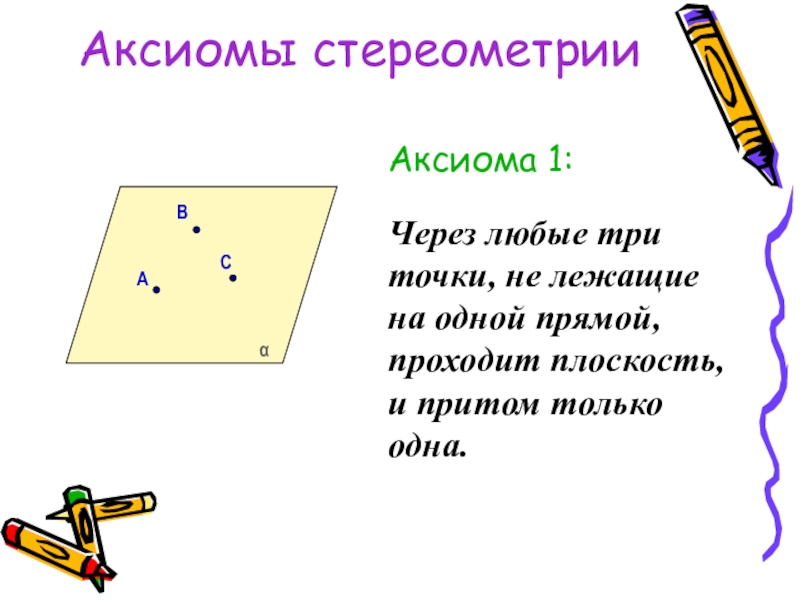
Слайд 6Аксиомы стереометрии
Аксиома 1:
Через любые три точки, не лежащие на одной прямой,
проходит плоскость, и притом только одна.
А
В
С
α
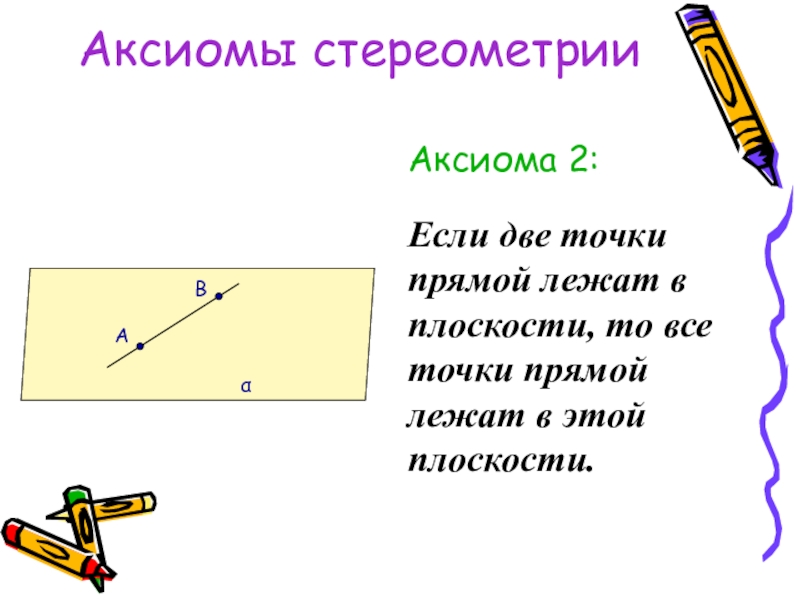
Слайд 7Аксиомы стереометрии
Аксиома 2:
Если две точки прямой лежат в плоскости, то все
точки прямой лежат в этой плоскости.
A
B
α
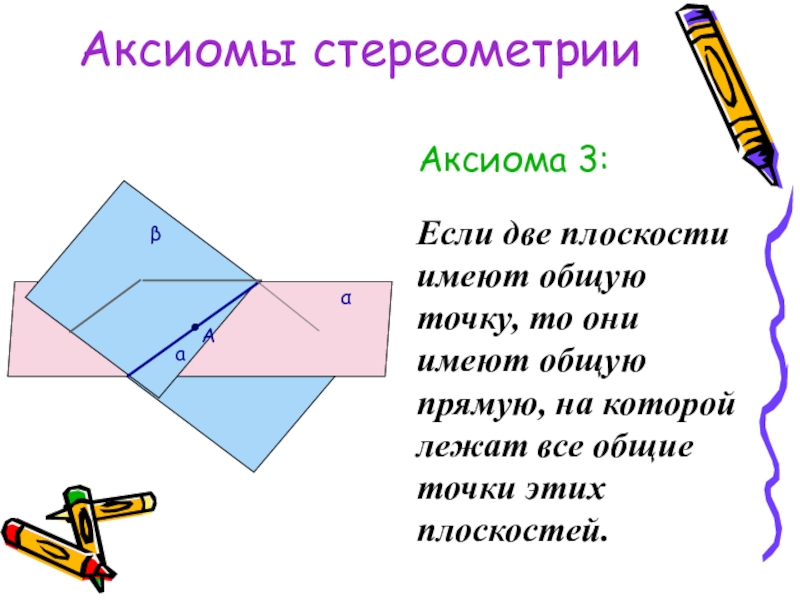
Слайд 8Аксиомы стереометрии
Аксиома 3:
Если две плоскости имеют общую точку, то они имеют
общую прямую, на которой лежат все общие точки этих плоскостей.
а
α
β
А
Слайд 9Некоторые
следствия из аксиом
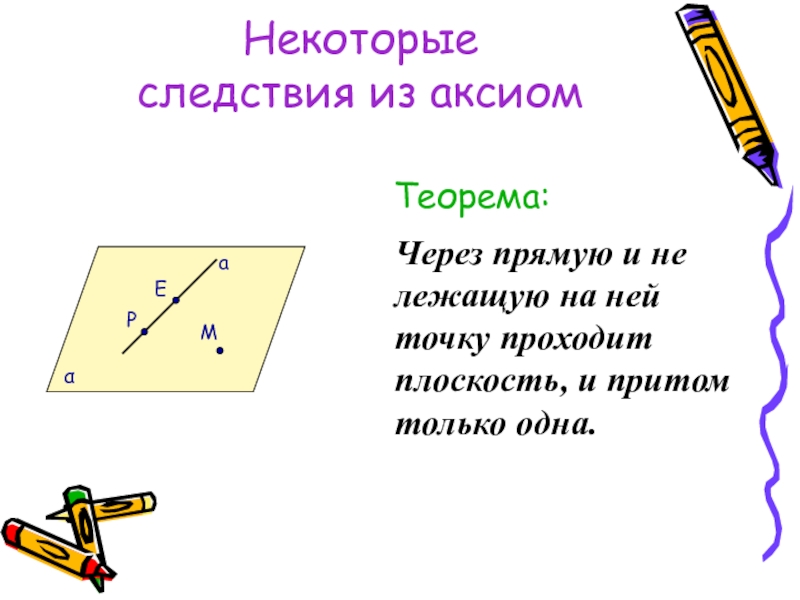
Теорема:
Через прямую и не лежащую на ней точку
проходит плоскость, и притом только одна.
a
E
P
M
α
Слайд 10Некоторые
следствия из аксиом
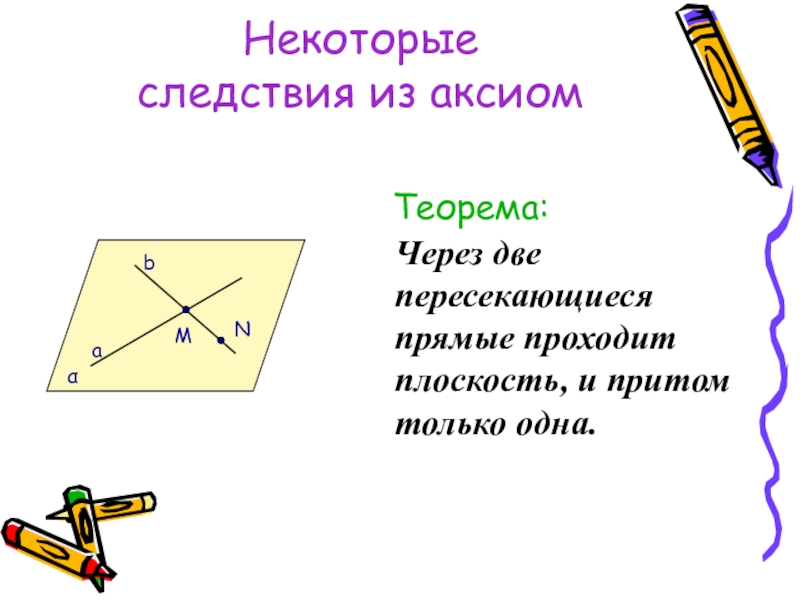
Теорема:
Через две пересекающиеся прямые проходит плоскость, и притом
только одна.
M
N
α
b
a
Слайд 12Параллельные
прямые в пространстве
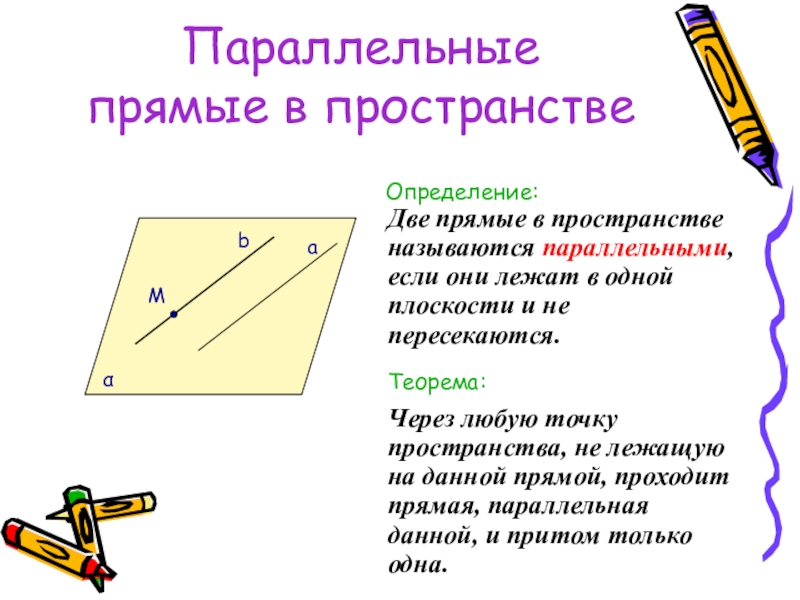
Определение:
Через любую точку пространства, не лежащую на данной
прямой, проходит прямая, параллельная данной, и притом только одна.
Две прямые в пространстве называются параллельными, если они лежат в одной плоскости и не пересекаются.
Теорема:
M
a
b
α
Слайд 13Параллельность
трех прямых
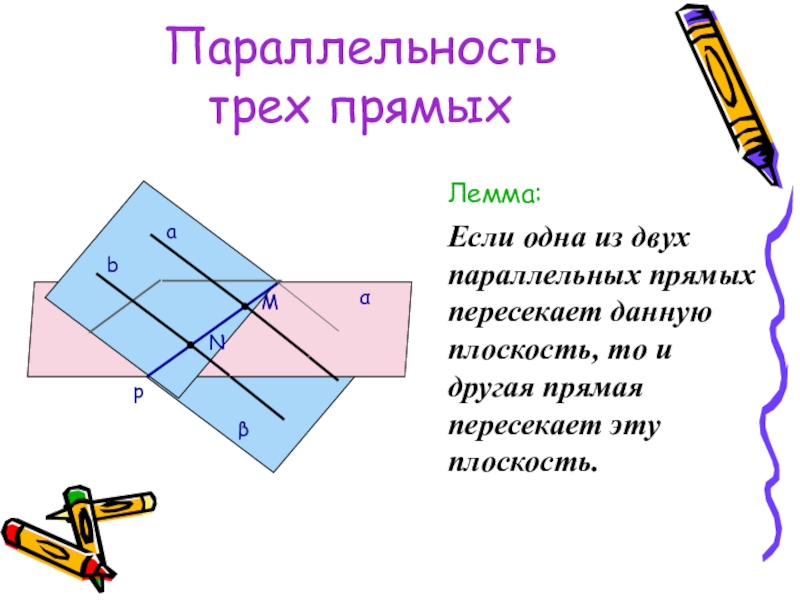
Лемма:
Если одна из двух параллельных прямых пересекает данную плоскость,
то и другая прямая пересекает эту плоскость.
а
α
β
b
p
N
M
Слайд 14Параллельность
трех прямых
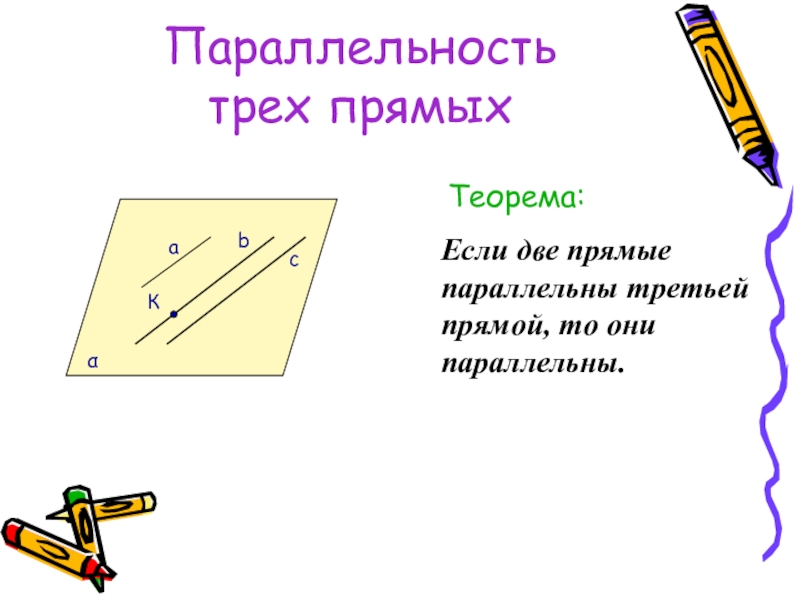
Теорема:
Если две прямые параллельны третьей прямой, то они параллельны.
К
a
b
α
c
Слайд 15Параллельность прямой и плоскости
Определение:
Прямая и плоскость называются параллельными, если они не
имеют общих точек.
α
b
a
Слайд 16Параллельность прямой и плоскости
Теорема:
Если прямая, не лежащая в данной плоскости, параллельна
какой-нибудь прямой, лежащей в этой плоскости, то она параллельна.
α
b
a
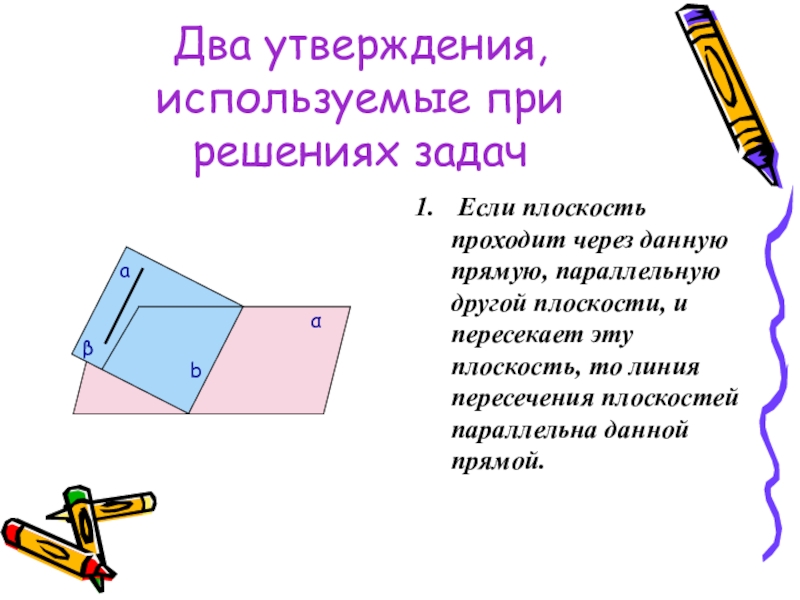
Слайд 17Два утверждения, используемые при решениях задач
Если плоскость проходит через данную
прямую, параллельную другой плоскости, и пересекает эту плоскость, то линия пересечения плоскостей параллельна данной прямой.
α
b
a
β
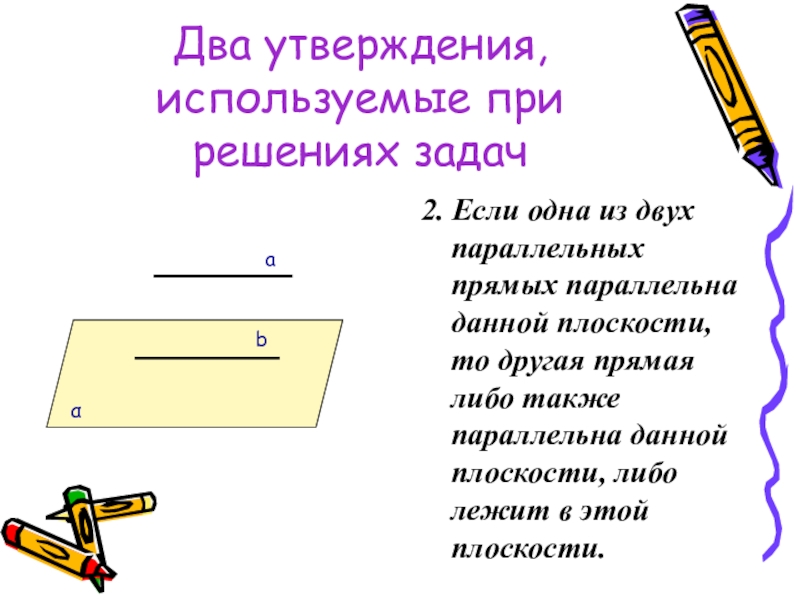
Слайд 18Два утверждения, используемые при решениях задач
2. Если одна из двух параллельных
прямых параллельна данной плоскости, то другая прямая либо также параллельна данной плоскости, либо лежит в этой плоскости.
α
b
a
Слайд 20Скрещивающиеся прямые
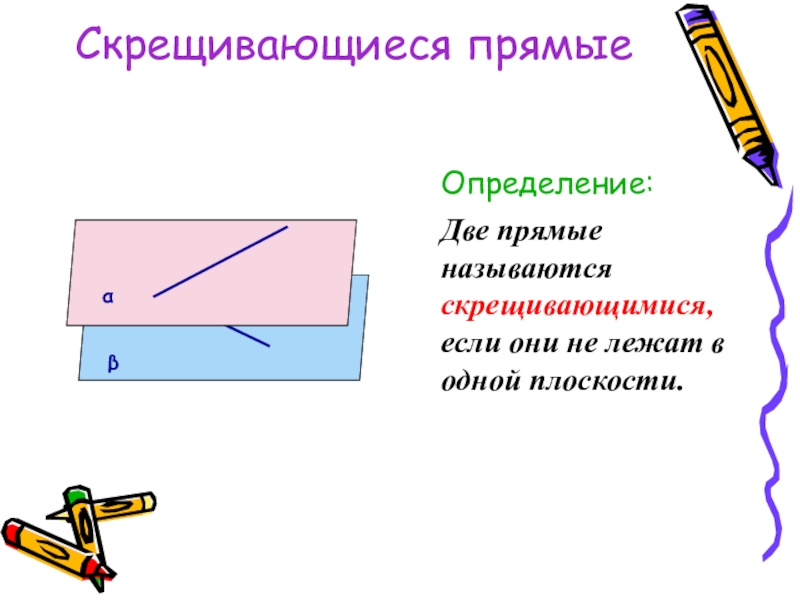
Определение:
Две прямые называются скрещивающимися, если они не лежат в одной
плоскости.
β
α
Слайд 21Признак
скрещивающихся прямых
Теорема:
Если одна из двух прямых лежит в некоторой плоскости, а
другая прямая пересекает эту плоскость в точке, не лежащей на первой прямой, то эти прямые скрещивающиеся.
А
В
α
D
C
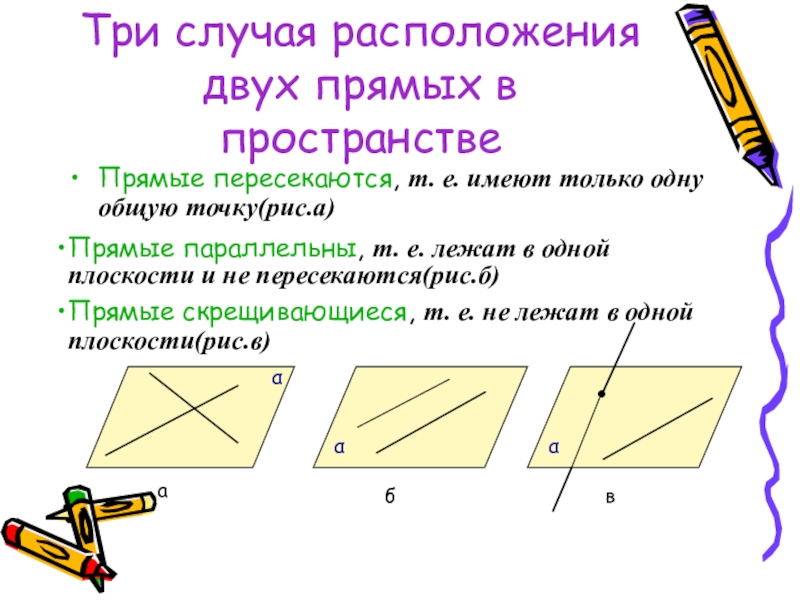
Слайд 22Три случая расположения двух прямых в пространстве
Прямые пересекаются, т. е. имеют
только одну общую точку(рис.а)
α
α
α
а
б
в
Прямые параллельны, т. е. лежат в одной плоскости и не пересекаются(рис.б)
Прямые скрещивающиеся, т. е. не лежат в одной плоскости(рис.в)
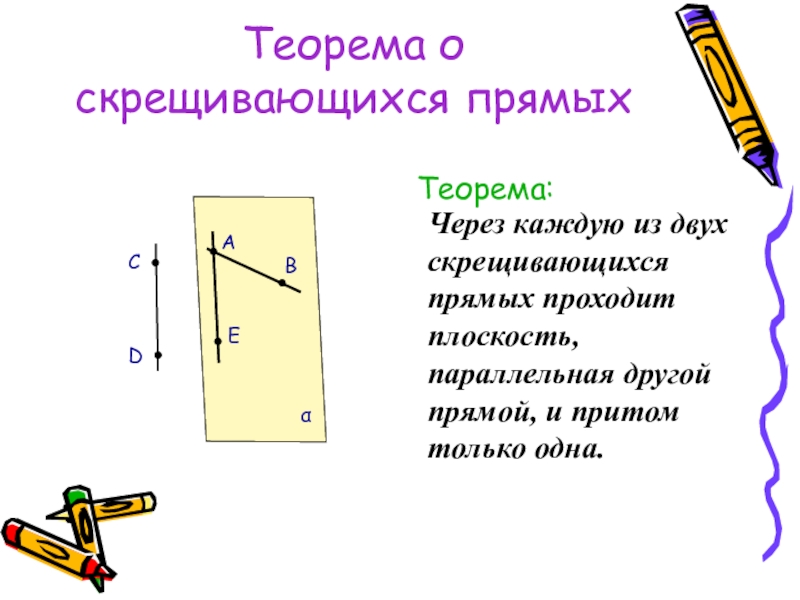
Слайд 23Теорема о скрещивающихся прямых
Теорема:
Через каждую из двух скрещивающихся прямых проходит плоскость,
параллельная другой прямой, и притом только одна.
α
B
A
E
D
C
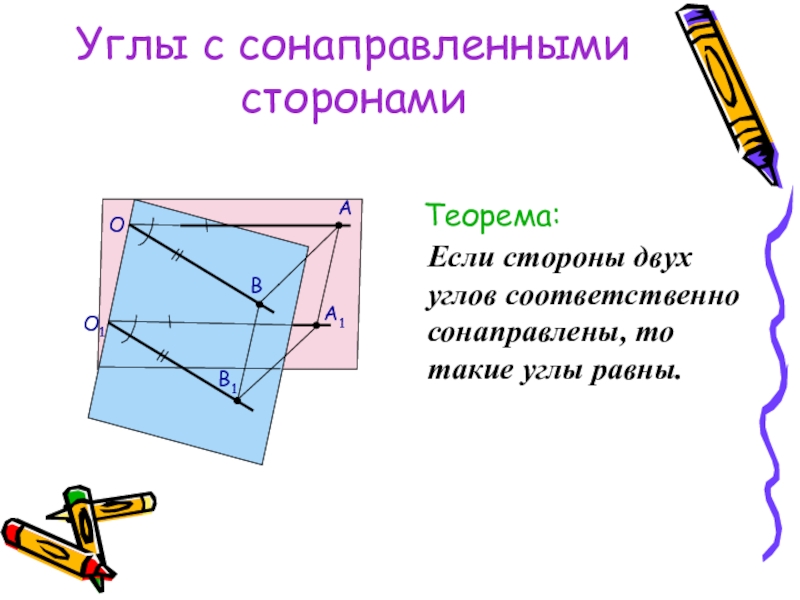
Слайд 24Углы с сонаправленными сторонами
Теорема:
Если стороны двух углов соответственно сонаправлены, то такие
углы равны.
O1
O
A
A1
B
B1
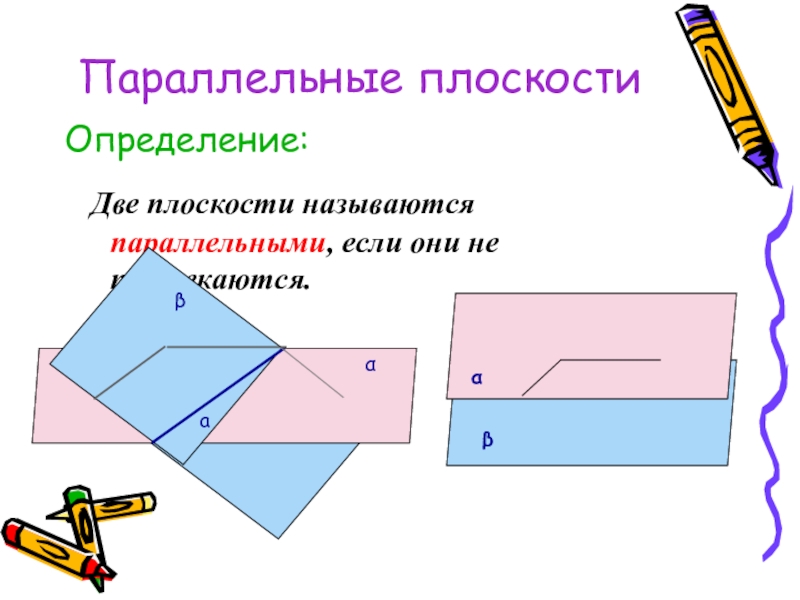
Слайд 26Параллельные плоскости
Две плоскости называются параллельными, если они не пересекаются.
Определение:
а
α
β
β
α
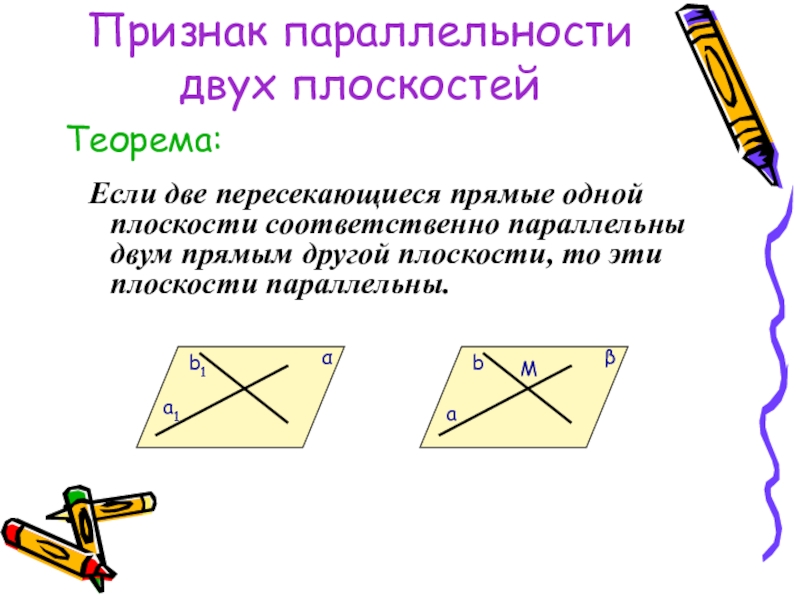
Слайд 27Признак параллельности двух плоскостей
Если две пересекающиеся прямые одной плоскости соответственно
параллельны двум прямым другой плоскости, то эти плоскости параллельны.
Теорема:
α
β
a1
b1
a
b
M
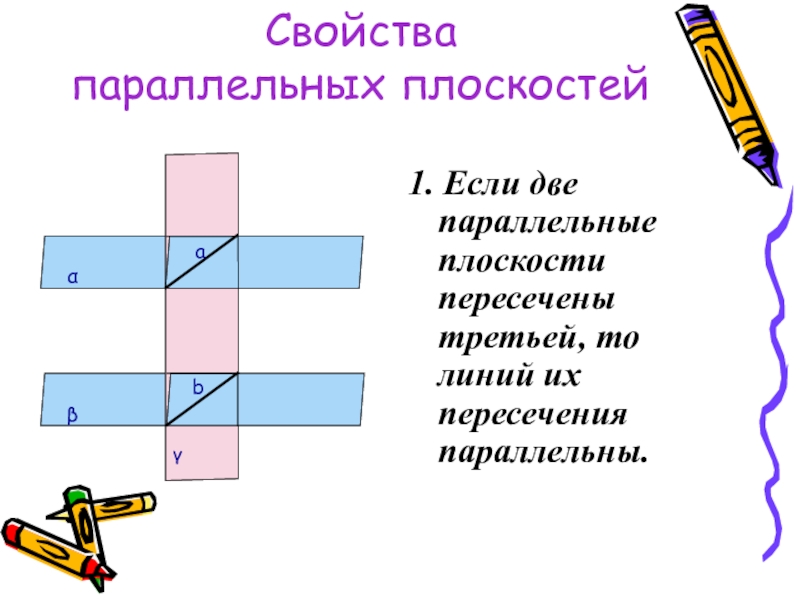
Слайд 28Свойства
параллельных плоскостей
1. Если две параллельные плоскости пересечены третьей, то линий
их пересечения параллельны.
β
α
γ
b
a
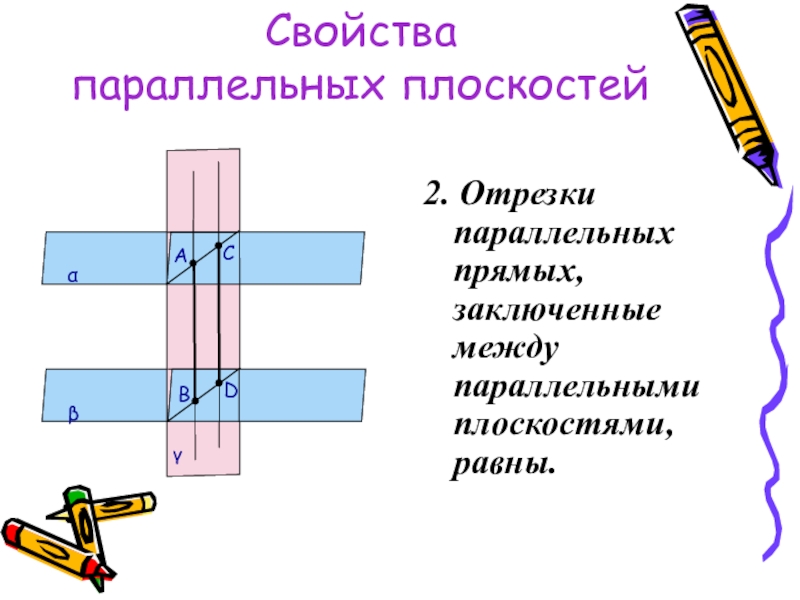
Слайд 29Свойства
параллельных плоскостей
2. Отрезки параллельных прямых, заключенные между параллельными плоскостями, равны.
β
α
γ
B
A
D
C
Слайд 31Перпендикулярные прямые в пространстве
Определение:
Две прямые в пространстве называются перпендикулярными (взаимно перпендикулярными),
если угол между ними равен 90°.
c
b
a
Слайд 32Перпендикулярные прямые в пространстве
Лемма:
Если одна из двух параллельных прямых перпендикулярна к
третьей прямой, то и другая прямая перпендикулярна к этой прямой.
A
c
C
b
a
M
Слайд 33Параллельные прямые,
перпендикулярные к плоскости
Определение:
Прямая называется перпендикулярной к плоскости, если она
перпендикулярна к любой прямой, лежащей в этой плоскости.
α
a
Слайд 34Параллельные прямые,
перпендикулярные к плоскости
Теорема:
Если одна из двух параллельных прямых перпендикулярна
к плоскости, то и другая прямая перпендикулярна к этой плоскости.
α
а
а1
x
Слайд 35Параллельные прямые,
перпендикулярные к плоскости
Теорема:
Если две прямые перпендикулярны к плоскости, то
они параллельны.
β
α
M
b
a
b1
c
Слайд 36Параллельные прямые,
перпендикулярные к плоскости
Теорема:
Если две прямые перпендикулярны к плоскости, то
они параллельны.
q
α
m
o
a
p
b
Слайд 37Теорема о прямой, перпендикулярной к плоскости
Теорема:
Через любую точку пространства проходит прямая,
перпендикулярная к данной плоскости, и притом только одна.
β
α
M
b
a
c
Слайд 39Расстояние
от точки до плоскости
Отрезок АН называется перпендикуляром, проведенным из точки
А к плоскости α, а точка Н – основанием перпендикуляра.
α
M
H
A
Слайд 40Расстояние
от точки до плоскости
АМ называется наклонной, проведенной из точки А
к плоскости α, а точка М – основанием наклонной.
Отрезок НМ называется проекцией наклонной на плоскость α.
АН – катет, сторона АМ – гипотенуза, поэтому АН<АМ.
Отрезок НМ называется проекцией наклонной на плоскость α.
АН – катет, сторона АМ – гипотенуза, поэтому АН<АМ.
α
M
H
A
Слайд 41Расстояние
от точки до плоскости
Перпендикуляр, проведенный из данной точки к плоскости,
меньше любой наклонной, проведенной из той же точки к этой плоскости.
α
M
H
A
Слайд 42Замечания
1. Расстояние от произвольной точки одной из параллельных плоскостей до другой
плоскости называется расстоянием между параллельными плоскостями.
2.Если прямая параллельна плоскости, то все точки прямой равноудалены от этой плоскости. В этом случае расстояние от произвольной точки прямой до плоскости называется расстоянием между прямой и параллельной ей плоскостью.
3. Расстояние между одной из скрещивающихся прямых и плоскостью, проходящей через другую прямую параллельно первой, называется расстоянием между скрещивающимися прямыми.
2.Если прямая параллельна плоскости, то все точки прямой равноудалены от этой плоскости. В этом случае расстояние от произвольной точки прямой до плоскости называется расстоянием между прямой и параллельной ей плоскостью.
3. Расстояние между одной из скрещивающихся прямых и плоскостью, проходящей через другую прямую параллельно первой, называется расстоянием между скрещивающимися прямыми.
Слайд 43Теорема о трех перпендикулярах
Теорема:
Прямая, проведенная в плоскости через основание наклонной перпендикулярно
к ее проекции на эту плоскость, перпендикулярна и к самой наклонной.
Обратная теорема:
Прямая, проведенная в плоскости через основание наклонной перпендикулярно к ней, перпендикулярна и к ее проекции
β
α
M
a
H
A
Слайд 44Угол между прямой и плоскостью
Определение:
Углом между прямой и плоскостью, пересекающей эту
прямую и не перпендикулярной к ней, называется угол между прямой и ее проекцией на плоскость.
α
A
M
ϕ0
ϕ
Слайд 45Угол между прямой и плоскостью
Проекцией точки на плоскость называется основание перпендикуляра,
проведенного из этой точки к плоскости, если точка не лежит в плоскости, и сама точка, если она лежит в плоскости.
α
M
M1
N
F1
F
Слайд 46Угол между прямой и плоскостью
Проекцией прямой на плоскость, не перпендикулярную к
этой прямой, является прямая.
β
α
H1
a
H
a1
M
Слайд 48Двугранный угол
Определение:
a
Двугранным углом называется фигура, образованная прямой а и двумя полуплоскостями
с общей границей а, не принадлежащими одной плоскости.
Слайд 49Двугранный угол
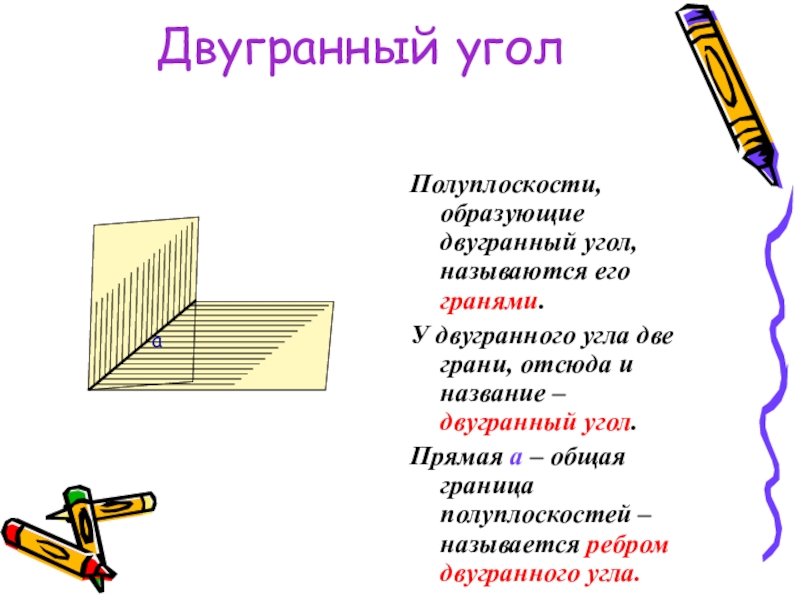
Полуплоскости, образующие двугранный угол, называются его гранями.
У двугранного угла две
грани, отсюда и название – двугранный угол.
Прямая а – общая граница полуплоскостей – называется ребром двугранного угла.
Прямая а – общая граница полуплоскостей – называется ребром двугранного угла.
a
Слайд 50Двугранный угол
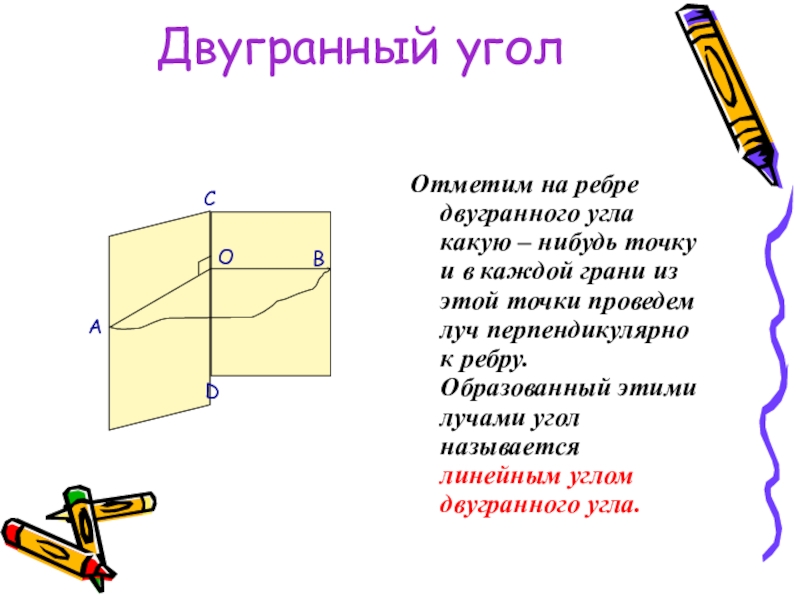
Отметим на ребре двугранного угла какую – нибудь точку и
в каждой грани из этой точки проведем луч перпендикулярно к ребру. Образованный этими лучами угол называется линейным углом двугранного угла.
A
C
O
B
D
Слайд 51Двугранный угол
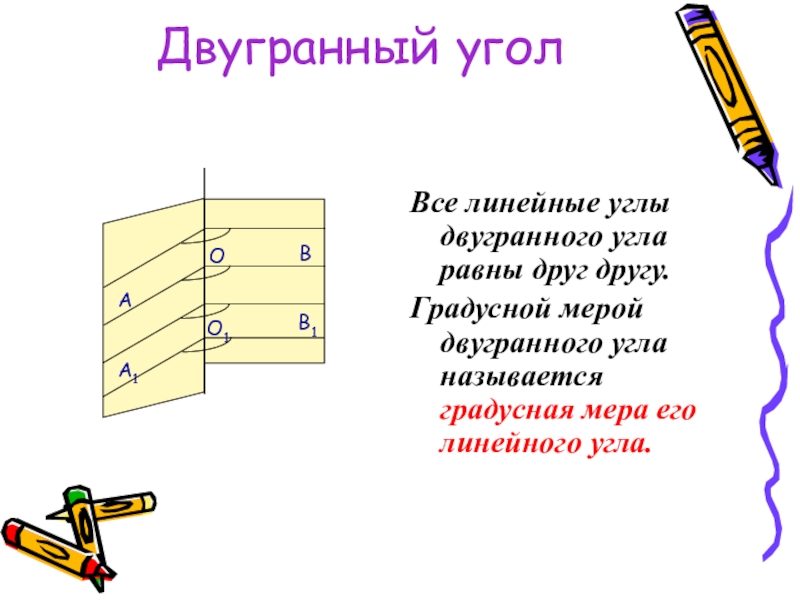
Все линейные углы двугранного угла равны друг другу.
Градусной мерой двугранного
угла называется градусная мера его линейного угла.
A
O
B
O1
B1
A1
Слайд 52Виды двугранных углов
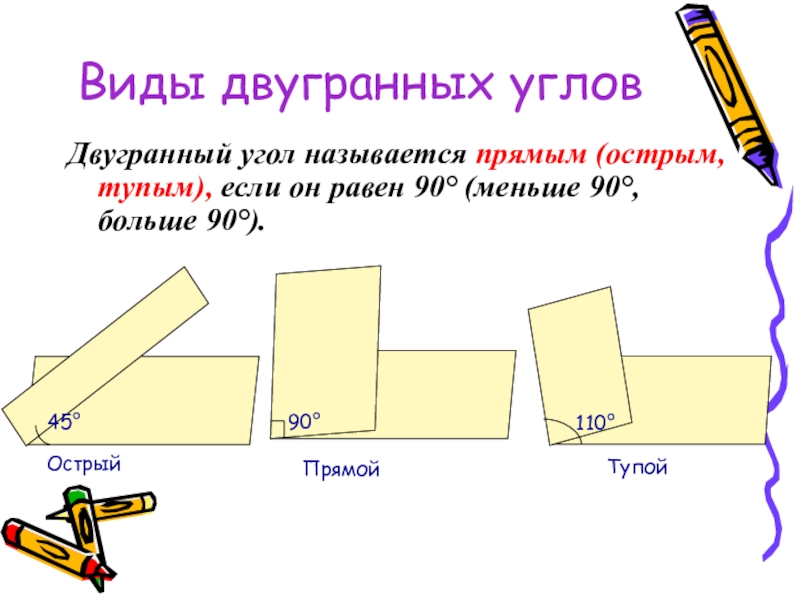
Двугранный угол называется прямым (острым, тупым), если он равен
90° (меньше 90°, больше 90°).
90°
45°
110°
Прямой
Тупой
Острый
Слайд 53Признак перпендикулярности двух плоскостей
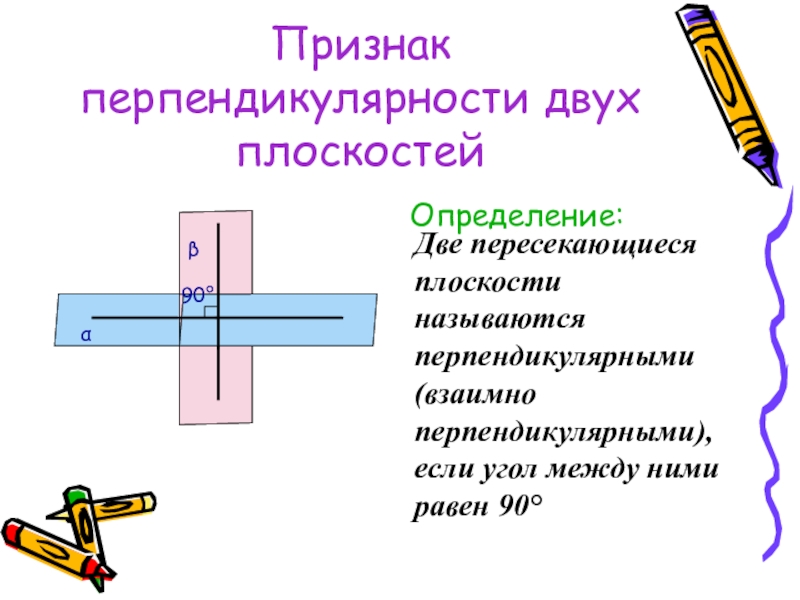
Определение:
Две пересекающиеся плоскости называются перпендикулярными (взаимно перпендикулярными), если
угол между ними равен 90°
β
α
90°
Слайд 54Признак перпендикулярности двух плоскостей
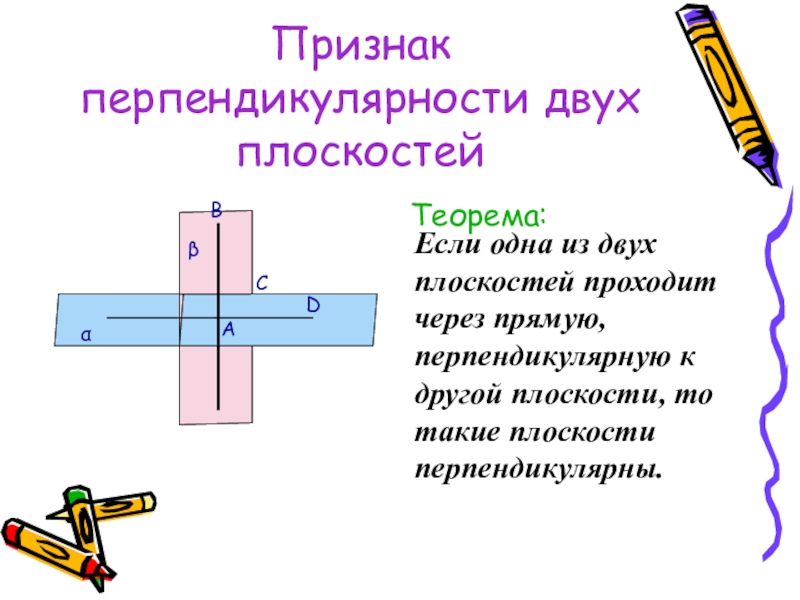
Теорема:
Если одна из двух плоскостей проходит через прямую,
перпендикулярную к другой плоскости, то такие плоскости перпендикулярны.
β
α
A
C
B
D
Слайд 55Признак перпендикулярности двух плоскостей
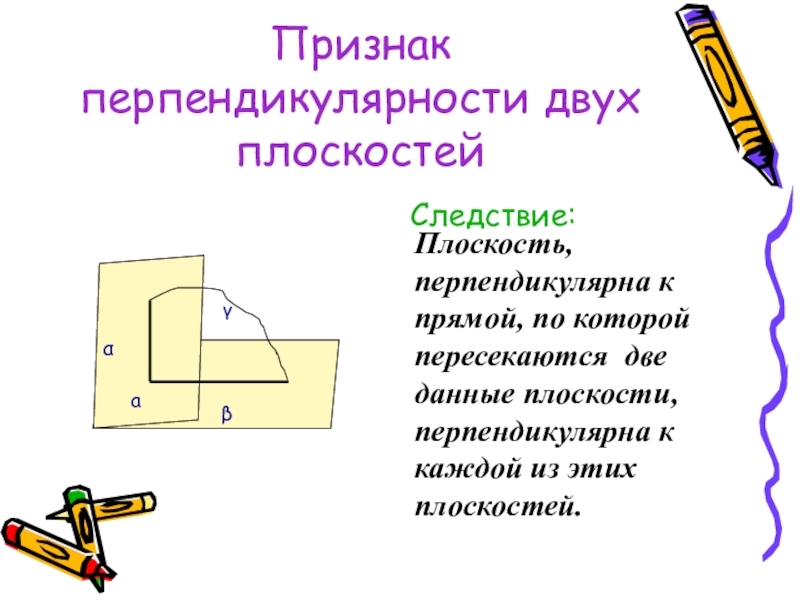
Следствие:
Плоскость, перпендикулярна к прямой, по которой пересекаются две
данные плоскости, перпендикулярна к каждой из этих плоскостей.
β
γ
α
а
