- Главная
- Разное
- Образование
- Спорт
- Естествознание
- Природоведение
- Религиоведение
- Французский язык
- Черчение
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, фоны, картинки для презентаций
- Экология
- Экономика
Презентация, доклад Двугранный угол (Геометрия 10 класс)
Содержание
- 1. Презентация Двугранный угол (Геометрия 10 класс)
- 2. ЦЕЛИ УРОКА:ВВЕСТИ ПОНЯТИЕ ДВУГРАННОГО УГЛА И ЕГО
- 3. 1.Что называют углом?2. Классифицируйте углы по градусной мере.3. Как называются углы, на рисунках?
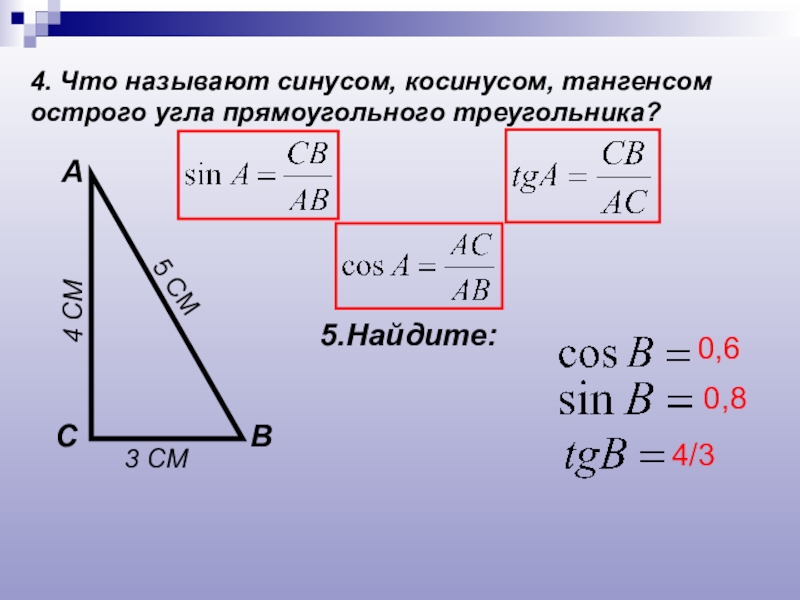
- 4. 4. Что называют синусом, косинусом, тангенсом острого угла прямоугольного треугольника?АВС5.Найдите:3 СМ4 СМ5 СМ0,60,84/3
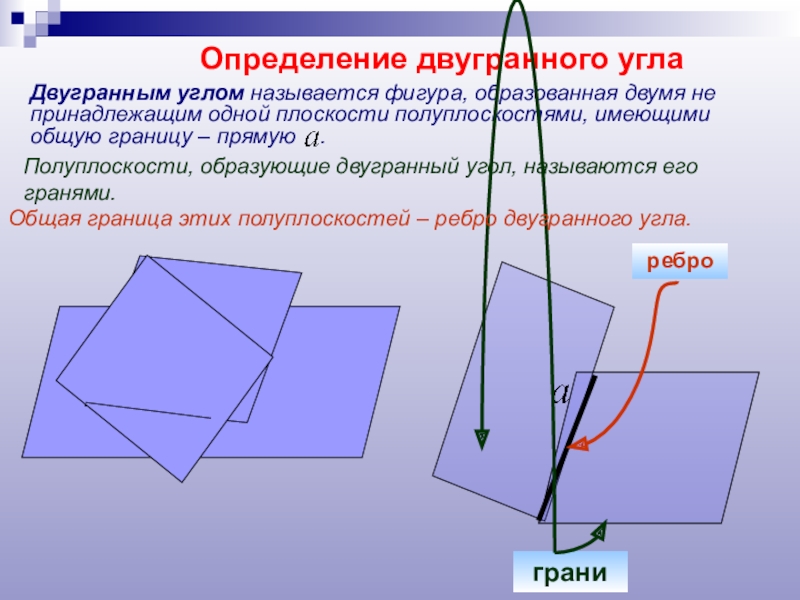
- 5. Определение двугранного углаДвугранным углом называется фигура, образованная
- 6. Обозначение двугранного угла.АВСDУгол CBDA
- 7. Назовите предметы, имеющие форму двугранного угла
- 8. Слайд 8
- 9. Измерение двугранных углов. Линейный угол.АВМDРСАВМС =РУгол Р
- 10. Линейным углом двугранного угла называется сечение двугранного угла плоскостью, перпендикулярной ребру.
- 11. Способ нахождения (построения) линейного угла.1. Найти (
- 12. Величина линейного угла не зависит от выбора его вершины на ребре двугранного угла.ABOA1O1B1
- 13. Двугранный угол является острым , прямым или
- 14. Аналогично тому , как и на плоскости , в пространстве определяются смежные и вертикальные двугранные углы.ββ1аαα1
- 15. геометрическая фигура, состоящая из двух полуплоскостей с общей границей, не развернутых в одну плоскостьDABCDBCADACBCADBCDBAADCBреброграниKDBAKDBCдвугранных углов нет
- 16. сечение двугранного угла плоскостью, перпендикулярной ребруот выбора
- 17. АС АСРи АСВпрямая СВ перпендикулярна ребру
- 18. АСАСРи АСВВ грани АСВпрямая ВО перпендикулярна
- 19. Задача №3КМРТА) Двугранный угол РТМК: (1)
- 20. Задача №3КМРТВАСАВ параллельна РТ (по построению), а
- 21. PKTMЗадача №3б) Двугранный угол РМКТ: (1) ребро
- 22. Задача №3TKPMв) Двугранный угол РТКМ: (1) ребро
- 23. Задача №3MPKTХУв) Двугранный угол РТКМ:3) Построим прямую
- 24. 1. В кубе A…D1 найдите угол между плоскостямиABC и CDD1.Ответ:
- 25. 2.В кубе A…D1 найдите угол между плоскостямиABC и CDA1.Ответ:
- 26. 3.В кубе A…D1 найдите угол между плоскостямиABC и BC1D.Ответ:О
- 27. В правильной пирамиде SABCD, все ребра которой равны 1, найдите угол между плоскостями SBC и ABC.
- 28. В тетраэдре ABCD, ребра которого равны 1, найдите угол между плоскостями ABC и BCD.ООтвет:
- 29. Ответ: 4. В кубе A…D1 найдите угол между плоскостямиBC1D и BA1D.
- 30. как поработали? – тема сложная, работать
- 31. Теоретические вопросы :Определение двугранного углаОпределение градусной меры
- 32. домашнее задание: 1. п.22, конспект2.
Слайд 2ЦЕЛИ УРОКА:
ВВЕСТИ ПОНЯТИЕ ДВУГРАННОГО УГЛА И ЕГО ЛИНЕЙНОГО УГЛА;
РАССМОТРЕТЬ ЗАДАЧИ НА
СФОРМИРОВАТЬ КОНСТРУКТИВНЫЙ НАВЫК НАХОЖДЕНИЯ УГЛА МЕЖДУ ПЛОСКОСТЯМИ.
Слайд 3
1.Что называют углом?
2. Классифицируйте углы по градусной мере.
3. Как называются углы,
Слайд 4
4. Что называют синусом, косинусом, тангенсом острого угла прямоугольного треугольника?
А
В
С
5.Найдите:
3 СМ
4
5 СМ
0,6
0,8
4/3
Слайд 5
Определение двугранного угла
Двугранным углом называется фигура, образованная двумя не принадлежащим одной
ребро
грани
Полуплоскости, образующие двугранный угол, называются его гранями.
Общая граница этих полуплоскостей – ребро двугранного угла.
Слайд 9
Измерение двугранных углов. Линейный угол.
А
В
М
D
Р
С
АВМС =
Р
Угол Р – линейный угол двугранного
Величиной двугранного угла называется величина его линейного угла.
Слайд 10Линейным углом двугранного угла называется сечение двугранного угла плоскостью, перпендикулярной ребру.
Слайд 11Способ нахождения (построения) линейного угла.
1. Найти ( увидеть) ребро и грани
2. В гранях найти направления ( прямые) перпендикулярные ребру
3. (при необходимости) заменить выбранные направления параллельными им лучами с общим началом на ребре двугранного угла
При изображении сохраняется параллельность и отношение длин параллельных отрезков
Слайд 12Величина линейного угла не зависит от выбора его вершины на ребре
A
B
O
A1
O1
B1
Слайд 13Двугранный угол является острым , прямым или тупым, если его линейный
α
β
Слайд 14Аналогично тому , как и на плоскости , в пространстве определяются
β
β1
а
α
α1
Слайд 15геометрическая фигура, состоящая из двух полуплоскостей с общей границей, не развернутых
DABC
DBCA
DACB
CADB
CDBA
ADCB
ребро
грани
KDBA
KDBC
двугранных углов нет
Слайд 16сечение двугранного угла плоскостью, перпендикулярной ребру
от выбора точки С на ребре
градусная мера соответствующего линейного угла
Найти ( увидеть) ребро и грани двугранного угла
В гранях найти направления ( прямые) перпендикулярные ребру
(при необходимости) заменить выбранные направления параллельными им лучами с общим началом на ребре двугранного угла
параллельность и отношение длин параллельных отрезков
Слайд 17АС
АСР
и АСВ
прямая СВ перпендикулярна ребру СА ( по условию)
В
В грани АСР
прямая СР перпендикулярна ребру СА
( по теореме о трех перпендикулярах)
угол РСВ - линейный для двугранного угла с ребром АС
Слайд 18АС
АСР
и АСВ
В грани АСВ
прямая ВО перпендикулярна ребру СА
( по
В грани АСР
прямая РК перпендикулярна ребру СА
( по теореме о трех перпендикулярах)
Угол РКВ - линейный для двугранного угла с РСАВ
К
Слайд 19Задача №3
К
М
Р
Т
А) Двугранный угол РТМК:
(1) ребро МТ,
(2) В грани МТР
прямая ТР перпендикулярна ребру МТ
( по определению прямой, перпендикулярной плоскости)
В грани МТК
прямая МК перпендикулярна ребру МТ
( по условию)
В
А
С
Слайд 20Задача №3
К
М
Р
Т
В
А
С
АВ параллельна РТ (по построению), а так как РТ перпендикулярна
Слайд 21P
K
T
M
Задача №3
б) Двугранный угол РМКТ:
(1) ребро МК, грани
(2) В грани МТК
прямая МТ перпендикулярна ребру МК ( по условию)
В грани МКР
прямая МР перпендикулярна ребру МК
( по теореме о трех перпендикулярах)
Ответ. Угол РМТ - линейный для двугранного угла с РМКТ
Слайд 22Задача №3
T
K
P
M
в) Двугранный угол РТКМ:
(1) ребро ТК, грани
(2) В грани МТК
прямая МХ, где Х – середина КТ, перпендикулярна ребру КТ ( по свойству равнобедренного треугольника)
Х
В грани КРТ
прямая РТ перпендикулярна ребру КТ
( по определению прямой перпендикулярной плоскости)
У
Слайд 23Задача №3
M
P
K
T
Х
У
в) Двугранный угол РТКМ:
3) Построим прямую УХ параллельно прямой РТ
(по лемме о связи параллельности и перпендикулярности)
Значит, искомый угол УХМ
Слайд 27В правильной пирамиде SABCD, все ребра которой равны 1, найдите угол
Слайд 30 как поработали?
– тема сложная, работать было
–работать было интересно, но есть
отдельные затруднения;
– мне было все понятно и интересно.
Как бы вы оценили свою работу?
Над чем нужно ещё работать?
Слайд 31Теоретические вопросы :
Определение двугранного угла
Определение градусной меры двугранного угла
Определение линейного угла
Утверждение о количестве линейных углов для данного двугранного
Способ построения линейного угла
Особенности изображения пространственных геометрических фигур на плоскости
Слайд 32 домашнее задание:
1. п.22, конспект
2. Оформить
3. Выучить теорию по вопросам конспекта.
Геометрия 10. тема « Двугранный угол»