- Главная
- Разное
- Образование
- Спорт
- Естествознание
- Природоведение
- Религиоведение
- Французский язык
- Черчение
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, фоны, картинки для презентаций
- Экология
- Экономика
Презентация, доклад Движение 9 класс геометрия
Содержание
- 1. Презентация Движение 9 класс геометрия
- 2. СодержаниеОпределениеВиды движенияСвойства движенияЗадачи на построениеПримеры движения в курсе алгебры Движение вокруг нас
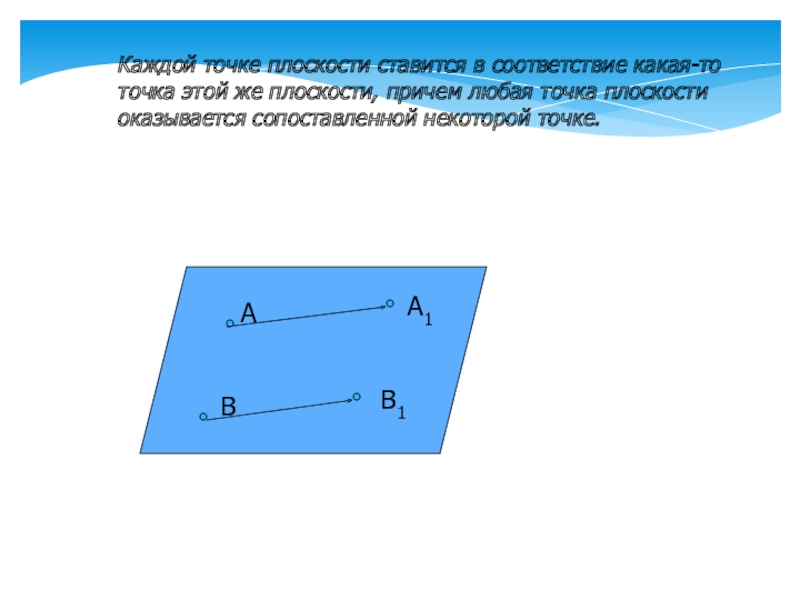
- 3. АА1ВВ1Каждой точке плоскости ставится в соответствие какая-то
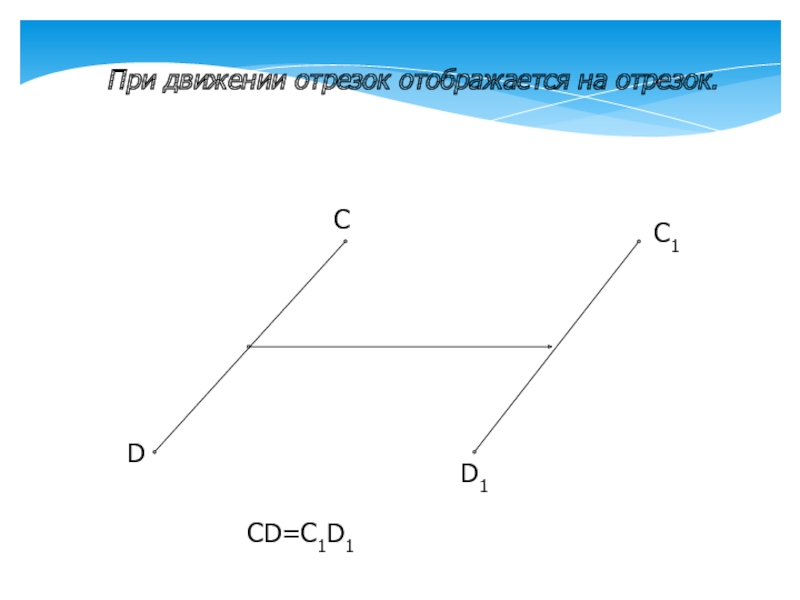
- 4. При движении отрезок отображается на отрезок.СDC1D1CD=C1D1
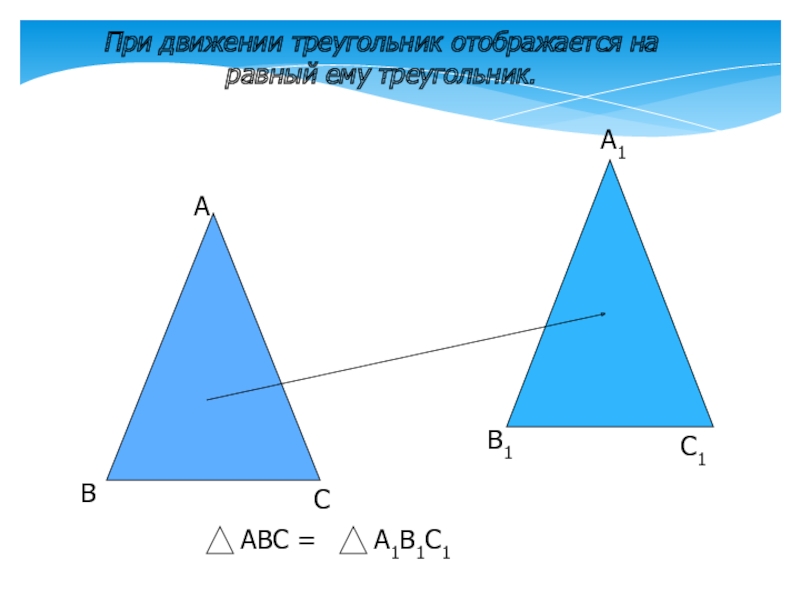
- 5. При движении треугольник отображается на равный ему треугольник.АВСА1В1С1АВС =А1В1С1
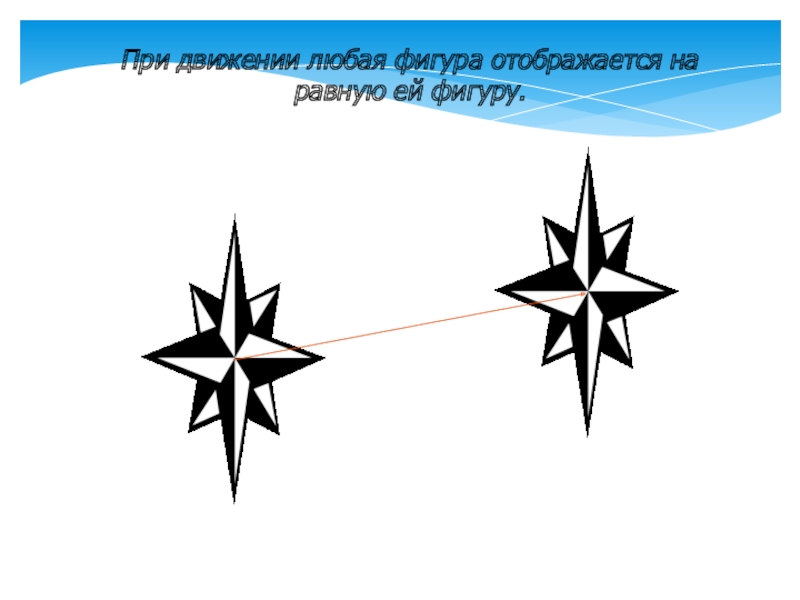
- 6. При движении любая фигура отображается на равную ей фигуру.
- 7. 1.Параллельный
- 8. 2.ПоворотABCB1A1Виды движенийАВС = А1В1С1Поворот является движением,
- 9. представляет поворот на 180 градусов. Пусть
- 10. 3.Центральная симметрияММ1NN1KK1OM1N1K1= MNKЦентральная, симметрия является движением изменяющим направления на противоположныеОсновное свойство центральной симметрии:
- 11. P1Q1S1= PQS4.Осевая симметрияPQSnP1Q1S1Точки P и P1
Слайд 2Содержание
Определение
Виды движения
Свойства движения
Задачи на построение
Примеры движения в курсе алгебры
Движение вокруг
Слайд 3
А
А1
В
В1
Каждой точке плоскости ставится в соответствие какая-то точка этой же плоскости,
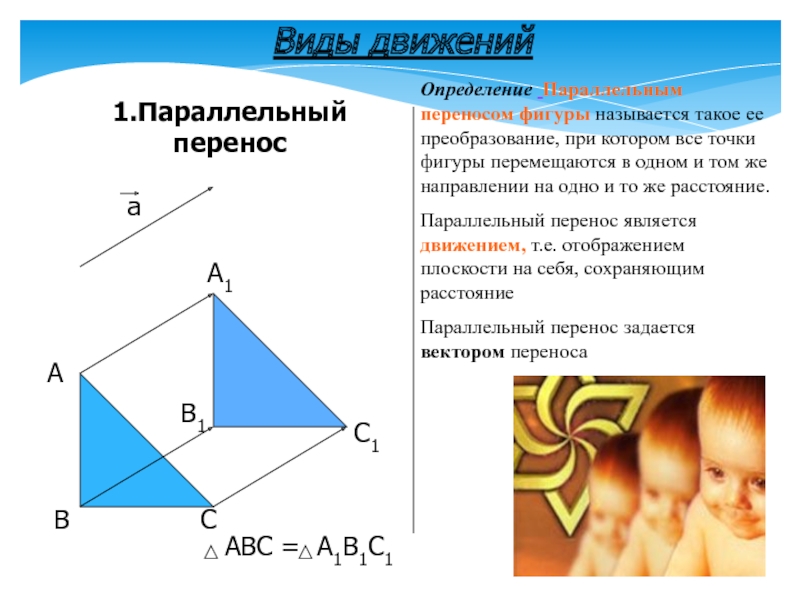
Слайд 71.Параллельный перенос
а
A
B
C
A1
B1
C1
Виды движений
АВС = А1В1С1
Определение
Параллельный перенос является движением, т.е. отображением плоскости на себя, сохраняющим расстояние
Параллельный перенос задается вектором переноса
Слайд 8
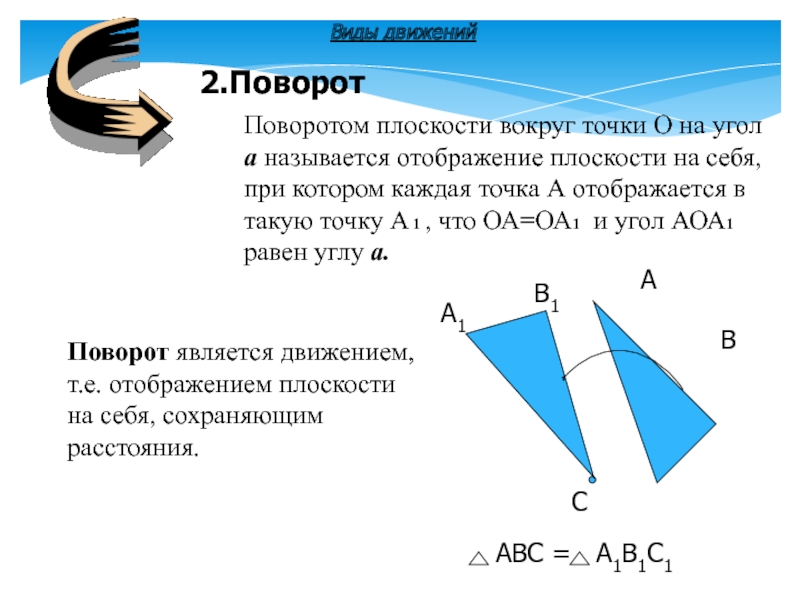
2.Поворот
A
B
C
B1
A1
Виды движений
АВС = А1В1С1
Поворот является движением, т.е. отображением плоскости на
Поворотом плоскости вокруг точки О на угол a называется отображение плоскости на себя, при котором каждая точка А отображается в такую точку А 1 , что ОА=ОА1 и угол АОА1 равен углу a.
Слайд 9 представляет поворот на 180 градусов. Пусть т.О – центр поворота.
ОХ1 = ОX.
Точки Х 1 и X называются симметричными относительно точки О.
Точка О - есть центр симметрии.
Х 1
Х
О
Особый случай
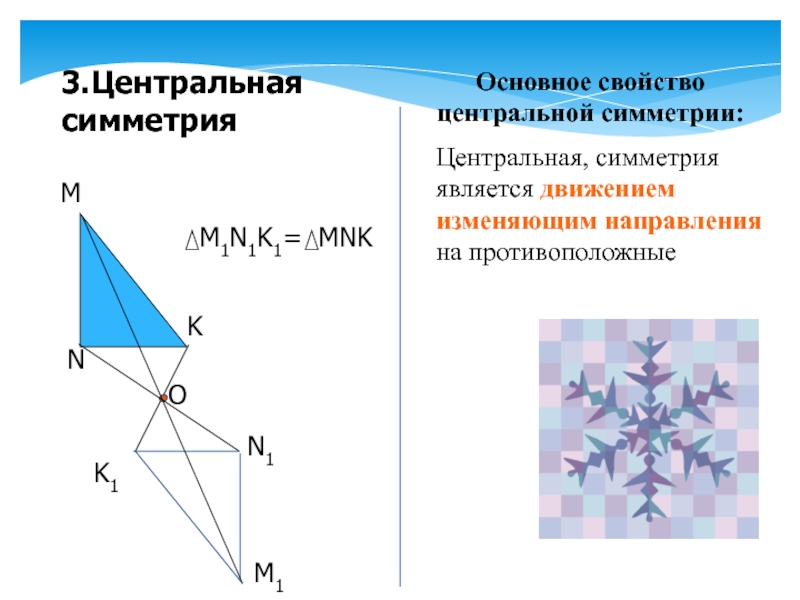
Слайд 103.Центральная симметрия
М
М1
N
N1
K
K1
O
M1N1K1= MNK
Центральная, симметрия является движением изменяющим направления на противоположные
Основное свойство
Слайд 11P1Q1S1= PQS
4.Осевая симметрия
P
Q
S
n
P1
Q1
S1
Точки P и P1 называются
Фигура F , полученная отражением фигуры F относительно прямой n, называется симметричной фигуре F относительно прямой n.
Осевая симметрия обладает следующим свойством – это отображение плоскости на себя, которое сохраняет расстояние между точками.