- Главная
- Разное
- Образование
- Спорт
- Естествознание
- Природоведение
- Религиоведение
- Французский язык
- Черчение
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, фоны, картинки для презентаций
- Экология
- Экономика
Презентация, доклад для подготовки к ЕГЭ
Содержание
- 1. Презентация для подготовки к ЕГЭ
- 2. Актуальность работыПри подготовке к ЕГЭ возникает проблема
- 3. Целью работы является обобщение и систематизация
- 4. В работе представлены методические материалы по
- 5. Материал работы рассчитан на 5 – 6
- 6. Содержание Введение
- 7. Литература Потоскуев Е.В. Геометрия. 10кл. : учеб.
- 8. Прямые в пространствеИз планиметрии известно, что на
- 9. Две прямые лежат в одной плоскости и
- 10. Угол между прямыми в пространстве.Величина угла между
- 11. прямые называются перпендикулярными, если угол между ними
- 12. Угол между прямыми в пространстве можно вычислитьФормулу
- 13. Задача 1. В кубе
- 14. Задача 2. В единичном кубе ABCDA1 B1
- 15. Задача 3. В кубе ABCDA1 B1 C1D1
- 16. Задачи для самостоятельного решения: В кубе ABCDA1
Актуальность работыПри подготовке к ЕГЭ возникает проблема систематизации и обобщении знаний учащихся по теме « Углы в пространстве». При организации итогового повторения в 11 классе необходимо систематизировать теоретический материал, обобщить методы решения задач, закрепить и проконтролировать
Слайд 2Актуальность работы
При подготовке к ЕГЭ возникает проблема систематизации и обобщении знаний
учащихся по теме « Углы в пространстве». При организации итогового повторения в 11 классе необходимо систематизировать теоретический материал, обобщить методы решения задач, закрепить и проконтролировать навыки решения задач. В результате ученики подготовятся к решению задач № 14 на нахождение углов между прямыми, между прямой и плоскостью, между плоскостями.
Слайд 3
Целью работы является обобщение и систематизация знаний учащихся по нахождению
углов в пространстве при подготовке к ЕГЭ. Для достижения поставленной цели необходимо решить следующие задачи:
Повторить теоретический материал по данной теме
Рассмотреть различные методы решения задач на нахождение углов
Закрепить навыки решения задач
Проверить знания
Повторить теоретический материал по данной теме
Рассмотреть различные методы решения задач на нахождение углов
Закрепить навыки решения задач
Проверить знания
Слайд 4
В работе представлены методические материалы по подготовке учащихся к решению
стереометрических задач на нахождение углов в пространстве, изложен теоретический материал, который необходимо повторить перед решением задач. Работа содержит разобранные задачи для коллективной работы, подборку задач для самостоятельного решения с ответами.
Слайд 5
Материал работы рассчитан на 5 – 6 часов, может быть использован
при подготовке к решению задач № 14 ЕГЭ в процессе повторения в 11 классе, изучающем математику на профильном уровне.
Слайд 6Содержание
Введение
Основная часть
1. Прямые в пространстве. Угол между прямыми.
2. Угол между прямой и плоскостью
3. Угол между двумя плоскостями
Заключение
Литература
Приложение1
Приложение2
Приложение3
Слайд 7Литература
Потоскуев Е.В. Геометрия. 10кл. : учеб. для общеобразоват. учреждений с углубленным
и профильным изучением математики / Е.В. Потоскуев, Л. И. Звавич. – 6-е изд.,стереотип. – М. : Дрофа, 2008
Потоскуев Е.В. Геометрия. 10кл. : задачник для общеобразоват. учреждений с углубленным и профильным изучением математики / Е.В. Потоскуев, Л. И. Звавич. – 2-е изд.,стереотип. – М. : Дрофа, 2004
Смирнова И.М. Геометрия. Расстояния и углы в пространстве: учебно - методическое пособие/ И.М. Смирнова, В.А. Смирнов – 2-е изд., перераб. и доп. – М.: Издательство « Экзамен», 2009
Корянов А.Г., Прокофьев А.П. Многогранники: виды задач и методы их решения /www. alexlarin. narod.ru – сайт по оказанию информационной поддержки студентам и абитуриентам при подготовке к ЕГЭ.
И.Ф. Шарыгин. Нужна ли школе 21-го века Геометрия?/ « Математика в школе» № 24 2004
Е. Потоскуев. Эффективные помощники « вхождения» в метрическую стереометрию / Математика. Приложение к Первое сентября № 22,23.
Смирнова Ирина Михайловна Цели обучения геометрии в школе geometry2006.narod.ru›Art/Aim.htm
Потоскуев Е.В. Геометрия. 10кл. : задачник для общеобразоват. учреждений с углубленным и профильным изучением математики / Е.В. Потоскуев, Л. И. Звавич. – 2-е изд.,стереотип. – М. : Дрофа, 2004
Смирнова И.М. Геометрия. Расстояния и углы в пространстве: учебно - методическое пособие/ И.М. Смирнова, В.А. Смирнов – 2-е изд., перераб. и доп. – М.: Издательство « Экзамен», 2009
Корянов А.Г., Прокофьев А.П. Многогранники: виды задач и методы их решения /www. alexlarin. narod.ru – сайт по оказанию информационной поддержки студентам и абитуриентам при подготовке к ЕГЭ.
И.Ф. Шарыгин. Нужна ли школе 21-го века Геометрия?/ « Математика в школе» № 24 2004
Е. Потоскуев. Эффективные помощники « вхождения» в метрическую стереометрию / Математика. Приложение к Первое сентября № 22,23.
Смирнова Ирина Михайловна Цели обучения геометрии в школе geometry2006.narod.ru›Art/Aim.htm
Слайд 8Прямые в пространстве
Из планиметрии известно, что на плоскости две прямые могут
либо пересекаться, либо не пересекаться ( быть параллельными). При этом речь идёт о таких прямых, которые заведомо лежат в одной плоскости. В стереометрии же, где фигуры рассматриваются в пространстве, для взаимного расположения двух прямых возможностей больше.
Слайд 9
Две прямые лежат в одной плоскости и имеют одну общую точку
– пересекающиеся прямые
Две прямые лежат в одной плоскости и не имеют общей точки – параллельные прямые
Две прямые не лежат в одной плоскости – скрещивающиеся прямые
Две прямые лежат в одной плоскости и не имеют общей точки – параллельные прямые
Две прямые не лежат в одной плоскости – скрещивающиеся прямые
Слайд 10Угол между прямыми в пространстве.
Величина угла между параллельными прямыми считается равной
нулю.
За величину угла между пересекающимися прямыми принимается величина наименьшего из углов, образованных этими прямыми.
Величина угла между скрещивающимися прямыми a и b определяется следующим образом. Через произвольную точку М пространства проводят прямые a1 || a и b1 || b и находят величину угла между пересекающимися прямыми a1 и b1. Эту величину и принимают за величину угла между скрещивающимися прямыми a и b
За величину угла между пересекающимися прямыми принимается величина наименьшего из углов, образованных этими прямыми.
Величина угла между скрещивающимися прямыми a и b определяется следующим образом. Через произвольную точку М пространства проводят прямые a1 || a и b1 || b и находят величину угла между пересекающимися прямыми a1 и b1. Эту величину и принимают за величину угла между скрещивающимися прямыми a и b
Слайд 11
прямые называются перпендикулярными, если угол между ними равен 90о.
Для установления
перпендикулярности скрещивающихся прямых используют следующую теорему о трех перпендикулярах.
Теорема. Если прямая, лежащая в плоскости, перпендикулярна ортогональной проекции наклонной к этой плоскости, то она перпендикулярна и самой наклонной.
Теорема. Если прямая, лежащая в плоскости, перпендикулярна ортогональной проекции наклонной к этой плоскости, то она перпендикулярна и самой наклонной.
Слайд 12Угол между прямыми в пространстве можно вычислить
Формулу
для нахождения угла
между прямыми m и l, если стороны a и b треугольника ABC соответственно параллельны этим прямым;
Формулу или в координатной форме
для нахождения угла между прямыми m и l, если векторы
параллельны соответственно этим прямым;
в частности для того чтобы прямые m и l были перпендикулярны, необходимо и достаточно, чтобы
.
между прямыми m и l, если стороны a и b треугольника ABC соответственно параллельны этим прямым;
Формулу или в координатной форме
для нахождения угла между прямыми m и l, если векторы
параллельны соответственно этим прямым;
в частности для того чтобы прямые m и l были перпендикулярны, необходимо и достаточно, чтобы
.
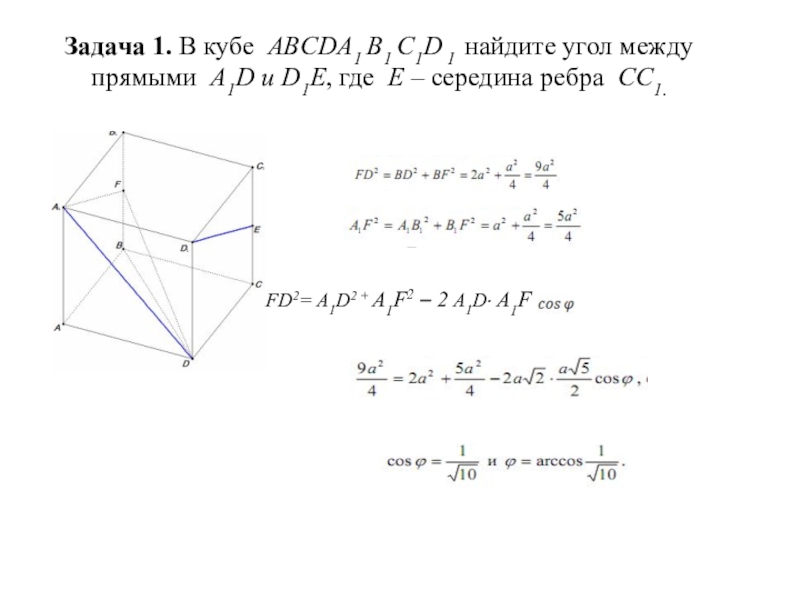
Слайд 13 Задача 1. В кубе ABCDA1 B1 C1D 1 найдите угол между
прямыми A1D и D1Е, где Е – середина ребра CC1.
FD2= A1D2 + A1F2 – 2 A1D· A1F
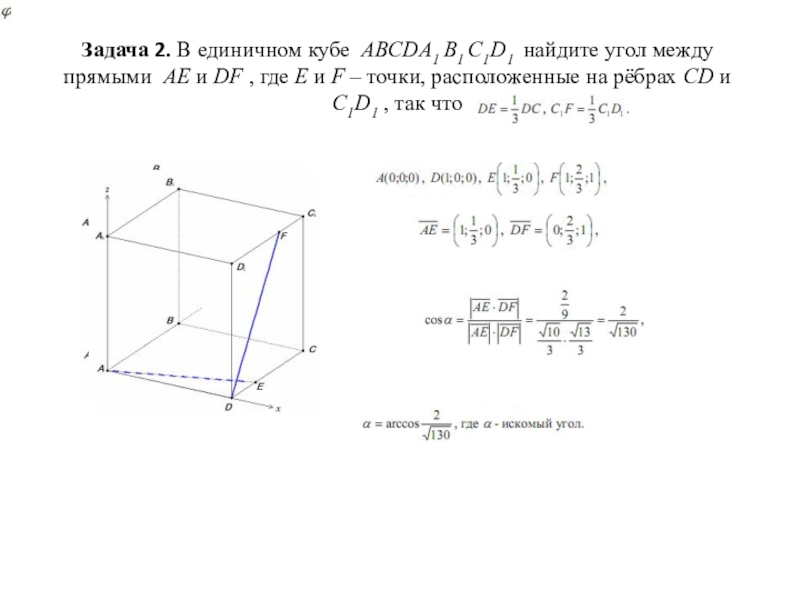
Слайд 14Задача 2. В единичном кубе ABCDA1 B1 C1D1 найдите угол между
прямыми AE и DF , где E и F – точки, расположенные на рёбрах CD и C1D1 , так что
Слайд 15Задача 3. В кубе ABCDA1 B1 C1D1 найдите угол между прямыми
EF и PQ, где E, F, P, Q - середины рёбер DD1, BC, AA1 B1C1 соответственно
Слайд 16Задачи для самостоятельного решения:
В кубе ABCDA1 B1 C1D1 точки E,F -
середины рёбер соответственно
Найдите косинус угла между прямыми AE и BF.
Ответ : 0,8
В правильной шестиугольной призме ABCD EFA1 B1 C1D1E1F1, все рёбра которой равны 1, найдите косинус угла между прямыми AB1 и BC1.
Ответ: 0,75
Найдите косинус угла между прямыми AE и BF.
Ответ : 0,8
В правильной шестиугольной призме ABCD EFA1 B1 C1D1E1F1, все рёбра которой равны 1, найдите косинус угла между прямыми AB1 и BC1.
Ответ: 0,75