- Главная
- Разное
- Образование
- Спорт
- Естествознание
- Природоведение
- Религиоведение
- Французский язык
- Черчение
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, фоны, картинки для презентаций
- Экология
- Экономика
Презентация, доклад на тему Построение сечений: практические задания
Содержание
- 1. Построение сечений: практические задания
- 2. Задача 1. Построить сечение куба ABCDA1B1C1D1
- 3. Построим след секущей плоскости на плоскость
- 4. Продолжим прямую EF, которая принадлежит сечению,
- 5. Прямая PG пересекает сторону AB в
- 6. Задача 2. Построить сечение четырехугольной призмы ABCDA1B1C1D1
- 7. Плоскости AA1D1D || BB1C1C, так как
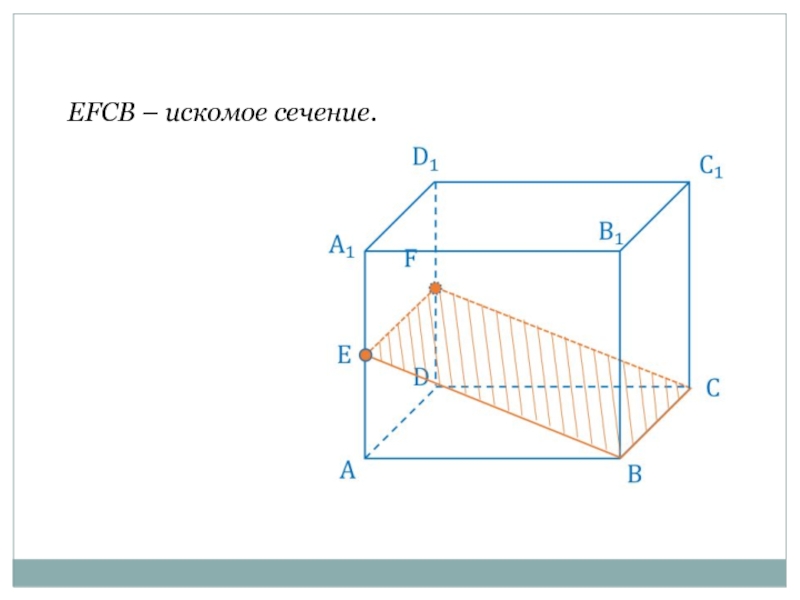
- 8. EFCB – искомое сечение.
- 9. Задача 3. Построить сечение прямоугольного параллепипеда ABCDA1B1C1D1,
- 10. Как в предыдущем примере, проведем прямые,
- 11. Задача 4. Построить сечение куба ABCDA1B1C1D1 ,
- 12. Продолжим прямую EF, которая принадлежит сечению,
- 13. Прямая PR – след секущей плоскости
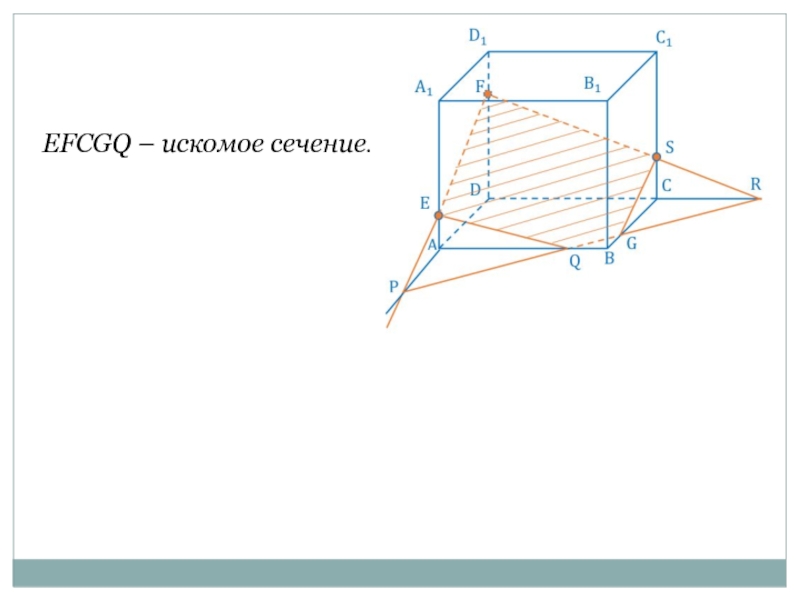
- 14. EFCGQ – искомое сечение.
Слайд 1Подготовил учитель математики,
МБОУ СОШ №12 города Воронежа,
Кузнецова Светлана Владимировна.
Построение сечений
Слайд 2Задача 1.
Построить сечение куба ABCDA1B1C1D1 плоскостью , проходящей через
AE : EA1 = 1 : 4
DF = FD1
CG : GD = 1 : 4
Плоскость пересекает многогранник по его внутренности. При этом пересечении данной плоскости с каждой гранью многогранника получится некоторый отрезок.
Таким образом, задача считается решенной, если найдены все отрезки, по которым плоскость пересекает грани многогранника.
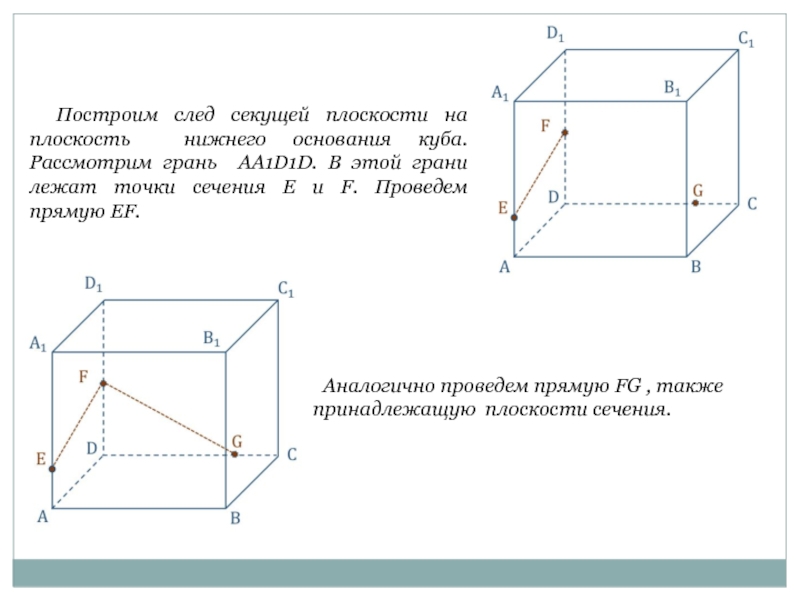
Слайд 3 Построим след секущей плоскости на плоскость нижнего основания куба. Рассмотрим
Аналогично проведем прямую FG , также принадлежащую плоскости сечения.
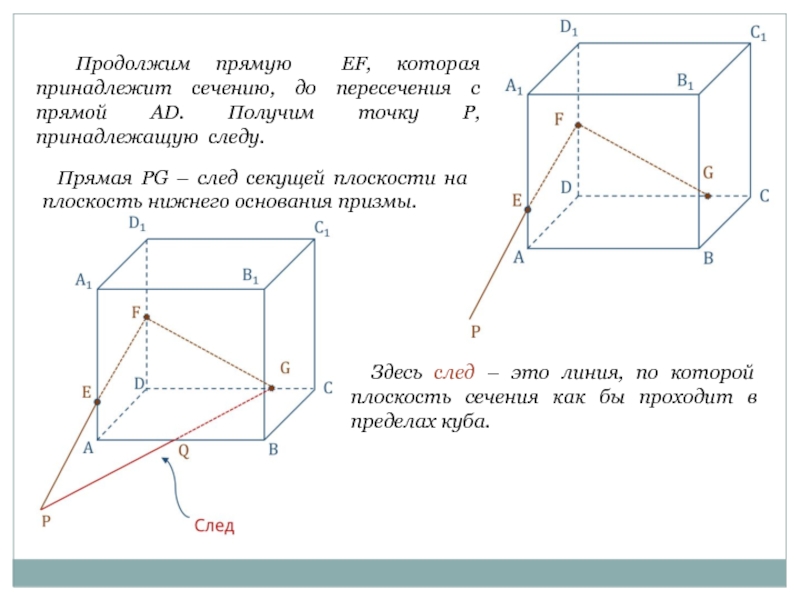
Слайд 4 Продолжим прямую EF, которая принадлежит сечению, до пересечения с прямой
Прямая PG – след секущей плоскости на плоскость нижнего основания призмы.
Здесь след – это линия, по которой плоскость сечения как бы проходит в пределах куба.
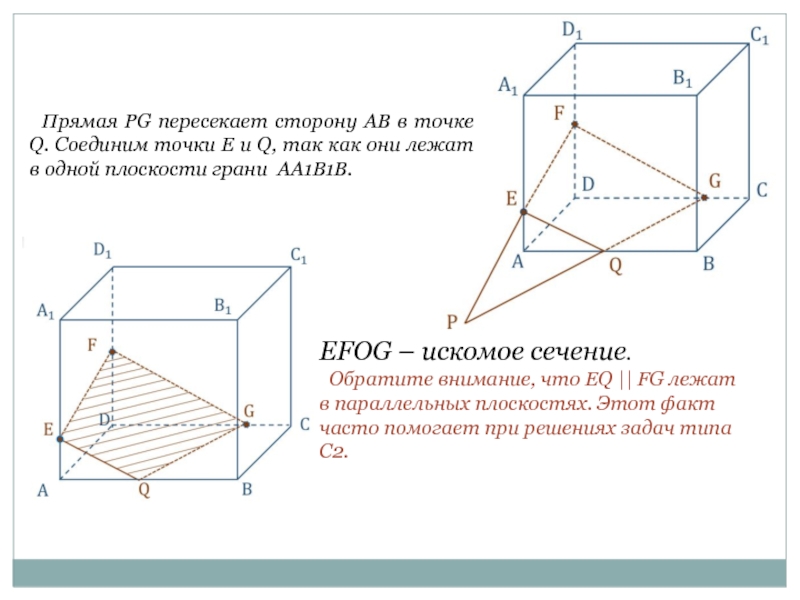
Слайд 5 Прямая PG пересекает сторону AB в точке Q. Соединим точки
EFOG – искомое сечение.
Обратите внимание, что EQ || FG лежат в параллельных плоскостях. Этот факт часто помогает при решениях задач типа С2.
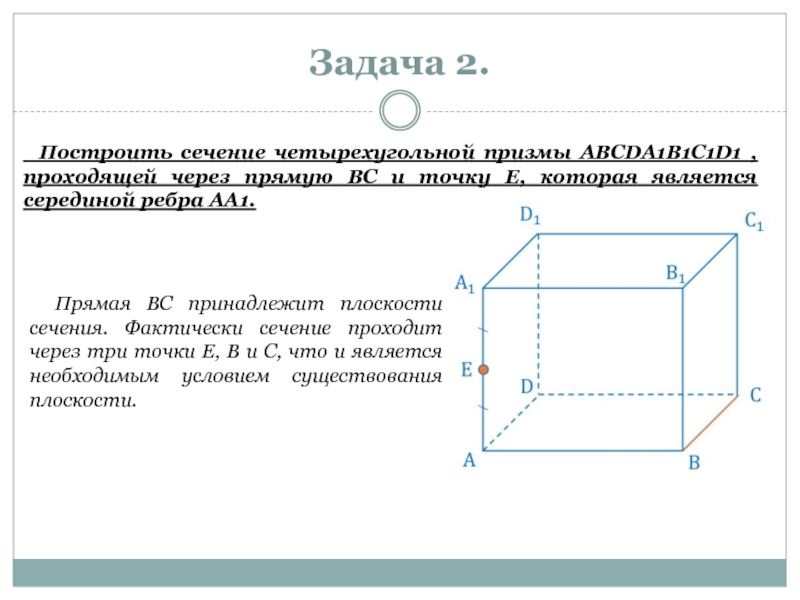
Слайд 6Задача 2.
Построить сечение четырехугольной призмы ABCDA1B1C1D1 , проходящей через прямую
Прямая BC принадлежит плоскости сечения. Фактически сечение проходит через три точки E, B и C, что и является необходимым условием существования плоскости.
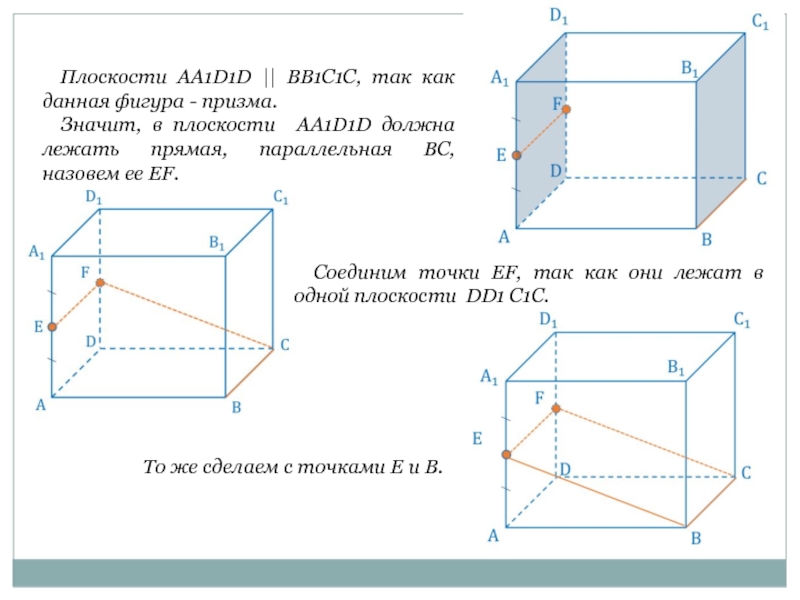
Слайд 7 Плоскости AA1D1D || BB1C1C, так как данная фигура - призма.
Значит, в плоскости AA1D1D должна лежать прямая, параллельная BC, назовем ее EF.
Соединим точки EF, так как они лежат в одной плоскости DD1 C1C.
То же сделаем с точками E и B.
Слайд 9Задача 3.
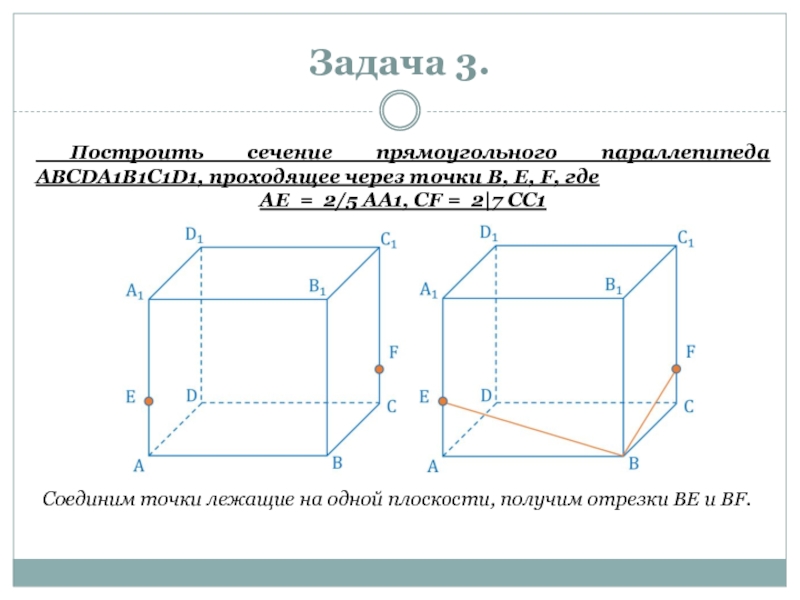
Построить сечение прямоугольного параллепипеда ABCDA1B1C1D1, проходящее через точки B,
AE = 2/5 AA1, CF = 2|7 CC1
Соединим точки лежащие на одной плоскости, получим отрезки BE и BF.
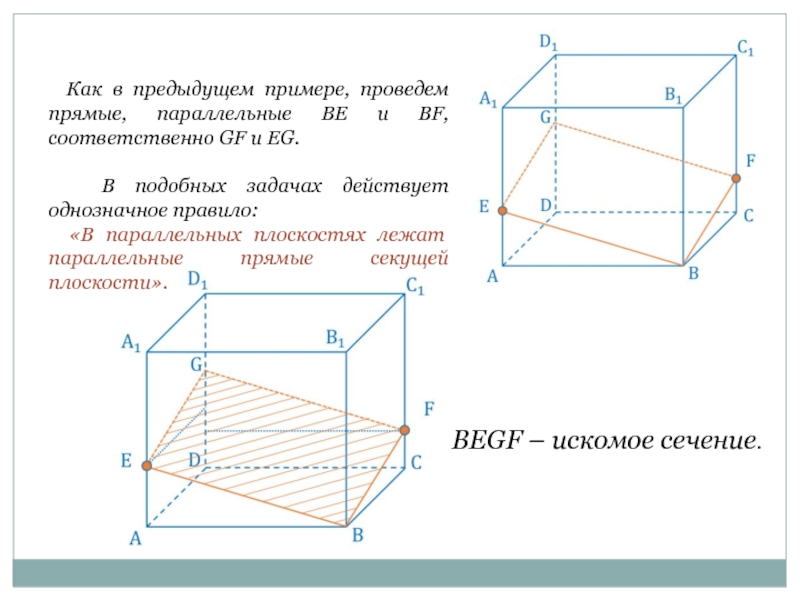
Слайд 10 Как в предыдущем примере, проведем прямые, параллельные BE и BF,
В подобных задачах действует однозначное правило:
«В параллельных плоскостях лежат параллельные прямые секущей плоскости».
BEGF – искомое сечение.
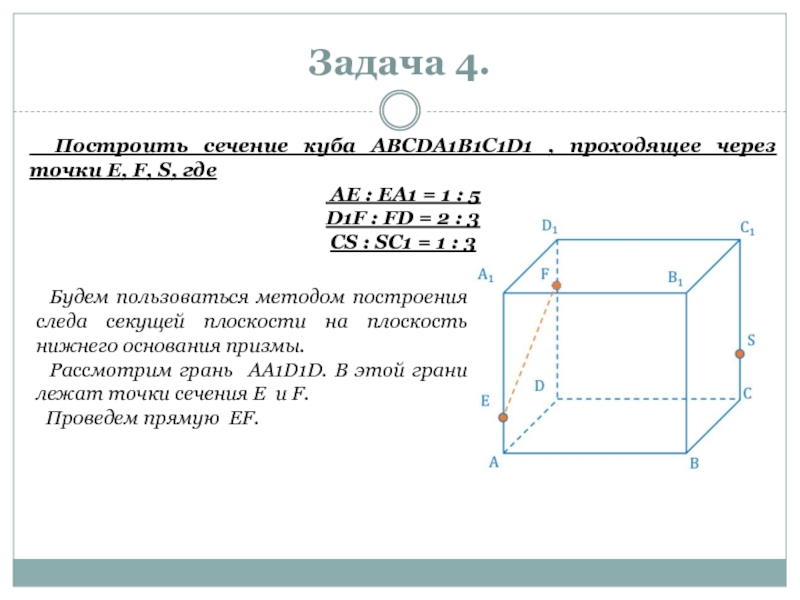
Слайд 11Задача 4.
Построить сечение куба ABCDA1B1C1D1 , проходящее через точки E,
AE : EA1 = 1 : 5
D1F : FD = 2 : 3
CS : SC1 = 1 : 3
Будем пользоваться методом построения следа секущей плоскости на плоскость нижнего основания призмы.
Рассмотрим грань AA1D1D. В этой грани лежат точки сечения E и F.
Проведем прямую EF.
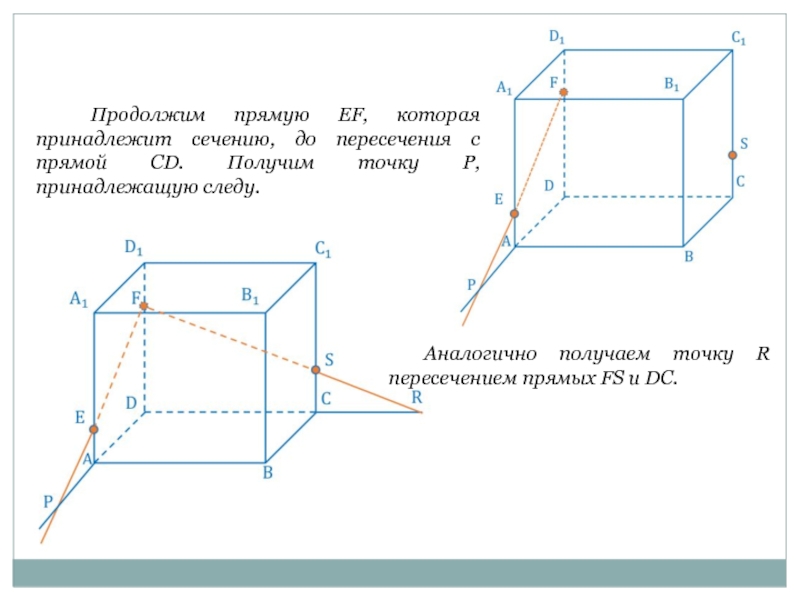
Слайд 12 Продолжим прямую EF, которая принадлежит сечению, до пересечения с прямой
Аналогично получаем точку R пересечением прямых FS и DC.
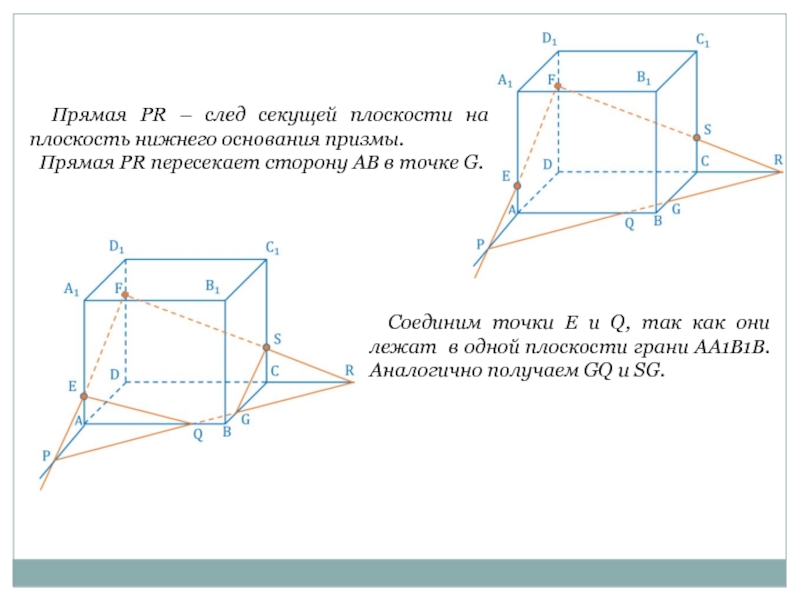
Слайд 13 Прямая PR – след секущей плоскости на плоскость нижнего основания
Прямая PR пересекает сторону AB в точке G.
Соединим точки E и Q, так как они лежат в одной плоскости грани AA1B1B. Аналогично получаем GQ и SG.