СОШ»
- Главная
- Разное
- Образование
- Спорт
- Естествознание
- Природоведение
- Религиоведение
- Французский язык
- Черчение
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, фоны, картинки для презентаций
- Экология
- Экономика
Презентация, доклад на тему Построение правильных многоугольников(9 класс)
Содержание
- 1. Построение правильных многоугольников(9 класс)
- 2. Правильные многоугольники уже в глубокой древности считались
- 3. Рассмотрим задачи, в которых нужно найти способы построения правильных многоугольников, вписанных в данную окружность.
- 4. Вписанный треугольник Впишите в данную окружность правильный треугольник.
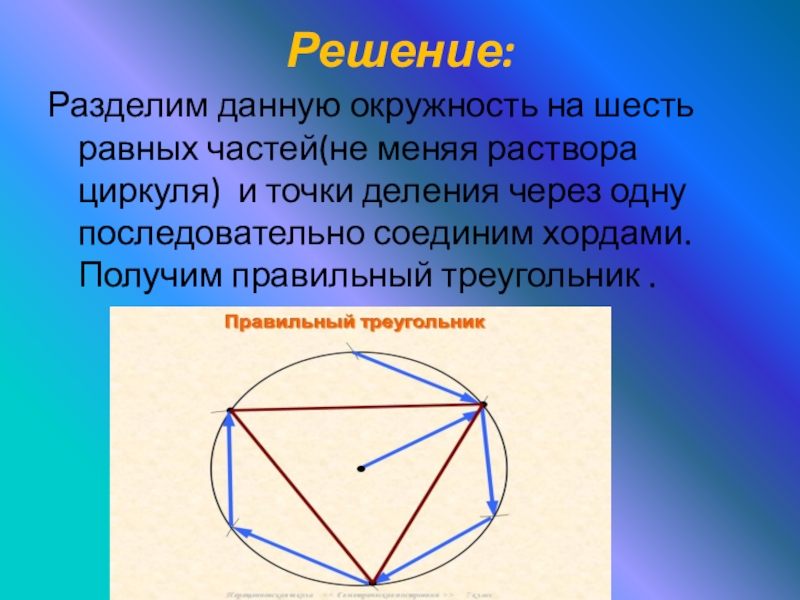
- 5. Решение:Разделим данную окружность на шесть равных частей(не
- 6. Вписанный квадрат Впишите в данную окружность квадрат.
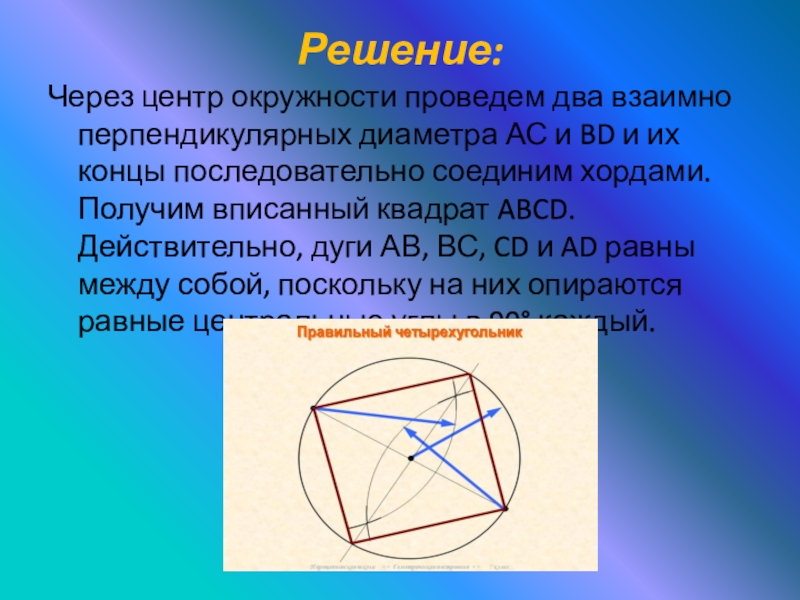
- 7. Решение:Через центр окружности проведем два взаимно перпендикулярных
- 8. Вписанный пятиугольник Впишите в данную окружность правильный пятиугольник
- 9. Решение:Постройте окружность, в которую будет вписан пятиугольник,
- 10. Слайд 10
- 11. Вписанный шестиугольник Впишите в данную окружность правильный шестиугольник.
- 12. Решение:Возьмем на данной окружности с центром О
- 13. Вписанный восьмиугольник Впишите в данную окружность правильный восьмиугольник.
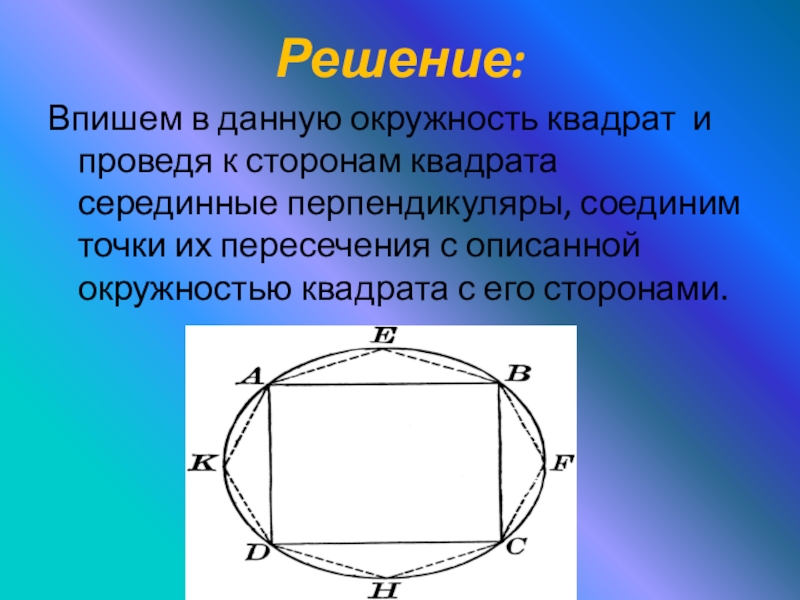
- 14. Решение:Впишем в данную окружность квадрат и проведя
- 15. Вписанный десятиугольник Докажите, что сторона правильного вписанного
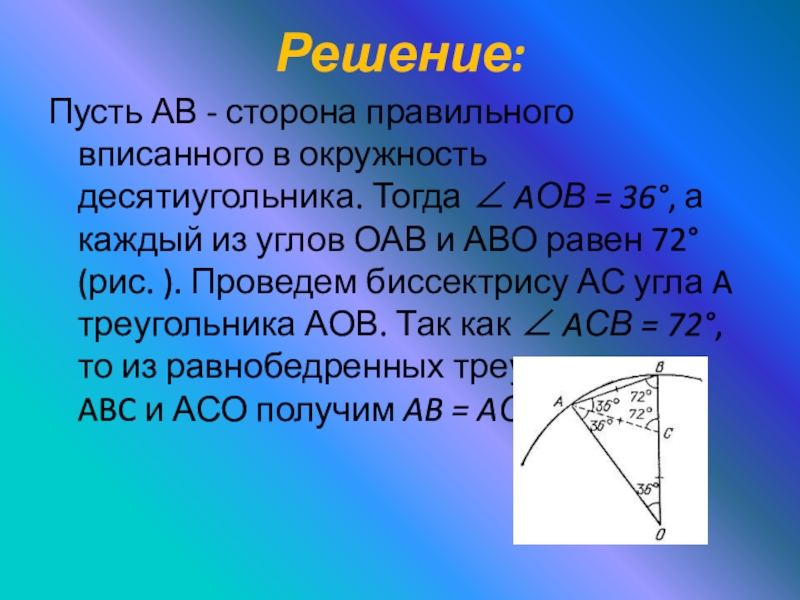
- 16. Решение:Пусть АВ - сторона правильного вписанного в
- 17. По свойству биссектрисы треугольника имеем ОС:ВС = АO:АВ. Поскольку АО
- 18. Вписанный двенадцатиугольник Впишите в данную окружность правильный двенадцатиугольник.
- 19. Решение:Удвоив число сторон правильного вписанного в
- 20. Вписанный пятнадцатиугольникВпишите в данную окружность правильный пятнадцатиугольник.
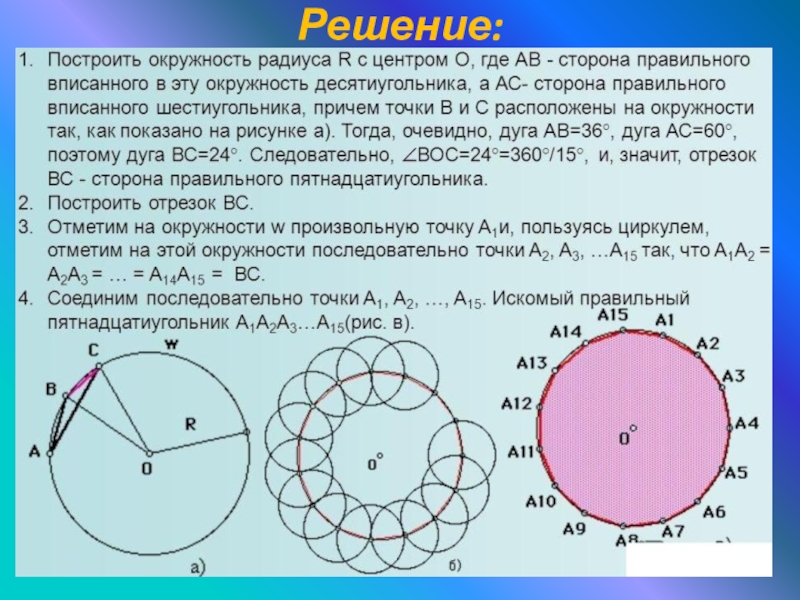
- 21. Решение:
- 22. Вписанный шестнадцатиугольник Впишите в данную окружность правильный шестнадцатиугольник.
- 23. Решение:Удвоив число сторон правильного вписанного в данную
- 24. Литература:«Примени математику»-И.Н.Сергеев, С.Н.Олехник, С.Б.Гашков, Москва «Наука», 1989г.Интернет- ресурсы.
Правильные многоугольники уже в глубокой древности считались символом красоты и совершенства. Это и понятно: ведь из всех многоугольников с заданным числом сторон наиболее приятен для глаза правильный многоугольник, у которого равны все стороны и равны все
Слайд 1Построение правильных многоугольников
Клещеногова В.А.- учитель математики МБОУ «Мордовско- Полянская
Слайд 2Правильные многоугольники уже в глубокой древности считались символом красоты и совершенства.
Это и понятно: ведь из всех многоугольников с заданным числом сторон наиболее приятен для глаза правильный многоугольник, у которого равны все стороны и равны все углы.
Слайд 3Рассмотрим задачи, в которых нужно найти способы построения правильных многоугольников, вписанных
в данную окружность.
Слайд 5Решение:
Разделим данную окружность на шесть равных частей(не меняя раствора циркуля) и
точки деления через одну последовательно соединим хордами. Получим правильный треугольник .
Слайд 7Решение:
Через центр окружности проведем два взаимно перпендикулярных диаметра АС и BD
и их концы последовательно соединим хордами. Получим вписанный квадрат ABCD. Действительно, дуги АВ, ВС, CD и AD равны между собой, поскольку на них опираются равные центральные углы в 90° каждый.
Слайд 9Решение:
Постройте окружность, в которую будет вписан пятиугольник, и обозначьте её центр
как O. (Это зелёная окружность на схеме справа).
Выберите на окружности точку A, которая будет одной из вершин пятиугольника. Постройте прямую через O и A.
Постройте прямую перпендикулярно прямой OA, проходящую через точку O. Обозначьте одно её пересечение с окружностью как точку B.
Постройте точку C посередине между O и B.
Проведите окружность с центром в точке C через точку A. Обозначьте её пересечение с прямой OB (внутри первоначальной окружности) как точку D.
Проведите окружность с центром в A через точку D, пересечение данной окружности с оригинальной (зелёной окружностью) обозначьте как точки E и F.
Проведите окружность с центром в E через точку A. Обозначьте её другое пересечение с первоначальной окружностью как точку G.
Проведите окружность с центром в F через точку A. Обозначьте её другое пересечение с первоначальной окружностью как точку H.
Постройте правильный пятиугольник AEGHF.
Выберите на окружности точку A, которая будет одной из вершин пятиугольника. Постройте прямую через O и A.
Постройте прямую перпендикулярно прямой OA, проходящую через точку O. Обозначьте одно её пересечение с окружностью как точку B.
Постройте точку C посередине между O и B.
Проведите окружность с центром в точке C через точку A. Обозначьте её пересечение с прямой OB (внутри первоначальной окружности) как точку D.
Проведите окружность с центром в A через точку D, пересечение данной окружности с оригинальной (зелёной окружностью) обозначьте как точки E и F.
Проведите окружность с центром в E через точку A. Обозначьте её другое пересечение с первоначальной окружностью как точку G.
Проведите окружность с центром в F через точку A. Обозначьте её другое пересечение с первоначальной окружностью как точку H.
Постройте правильный пятиугольник AEGHF.
Слайд 12Решение:
Возьмем на данной окружности с центром О произвольную точку A и
раствором циркуля, равным ОА, отложим на окружности последовательно еще пять точек В, C, D, Е и F. Точки A, В, С, D, Е и F являются вершинами правильного шестиугольника. В самом деле, соединив эти точки последовательно друг с другом и с точкой О, мы получим пять равносторонних треугольников (рис. ). Так как каждый из углов АОВ, ВОС, COD, DOE, EOF равен по 60°, то угол AOF также равен 60°, а, значит, окружность разделена на шесть равных дуг.
Слайд 14Решение:
Впишем в данную окружность квадрат и проведя к сторонам квадрата серединные
перпендикуляры, соединим точки их пересечения с описанной окружностью квадрата с его сторонами.
Слайд 15Вписанный десятиугольник
Докажите, что сторона правильного вписанного в окружность десятиугольника равна большей
части "золотого сечения";радиуса этой окружности. Впишите в данную окружность правильный десятиугольник.
Слайд 16Решение:
Пусть АВ - сторона правильного вписанного в окружность десятиугольника. Тогда ∠ AОВ
= 36°, а каждый из углов ОАВ и АВО равен 72° (рис. ). Проведем биссектрису АС угла A треугольника АОВ. Так как ∠ AСВ = 72°, то из равнобедренных треугольников ABC и АСО получим AB = AС = ОС.
Слайд 17По свойству биссектрисы треугольника имеем ОС:ВС = АO:АВ. Поскольку АО = ОВ, АВ =
ОС, то ОС:ВС = ОВ:ОС, т. е. ОС2= ВС*ОВ, а это и означает, что радиус ОВ разделен точкой С в "золотом сечении", причем ОС - большая часть радиуса (ибо ∠ ACB> ∠BAC, откуда ОС = АВ>ВС).
Таким образом, разделив радиус ОВ данной окружности в "золотом сечении» и взяв большую его часть ОС, мы найдем длину стороны А В правильного вписанного в эту окружность десятиугольника. Теперь от любой точки данной окружности последовательно отложим девять хорд, каждая из которых равна АВ. Один из конкретных способов построения стороны ОС = АВ требуемого десятиугольника приведен на рис.
Таким образом, разделив радиус ОВ данной окружности в "золотом сечении» и взяв большую его часть ОС, мы найдем длину стороны А В правильного вписанного в эту окружность десятиугольника. Теперь от любой точки данной окружности последовательно отложим девять хорд, каждая из которых равна АВ. Один из конкретных способов построения стороны ОС = АВ требуемого десятиугольника приведен на рис.
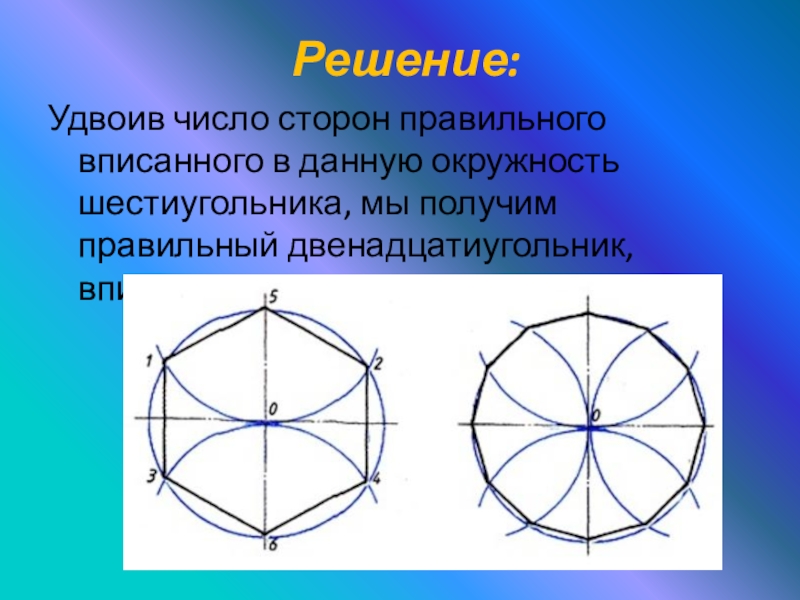
Слайд 19 Решение:
Удвоив число сторон правильного вписанного в данную окружность шестиугольника, мы
получим правильный двенадцатиугольник, вписанный в ту же окружность .
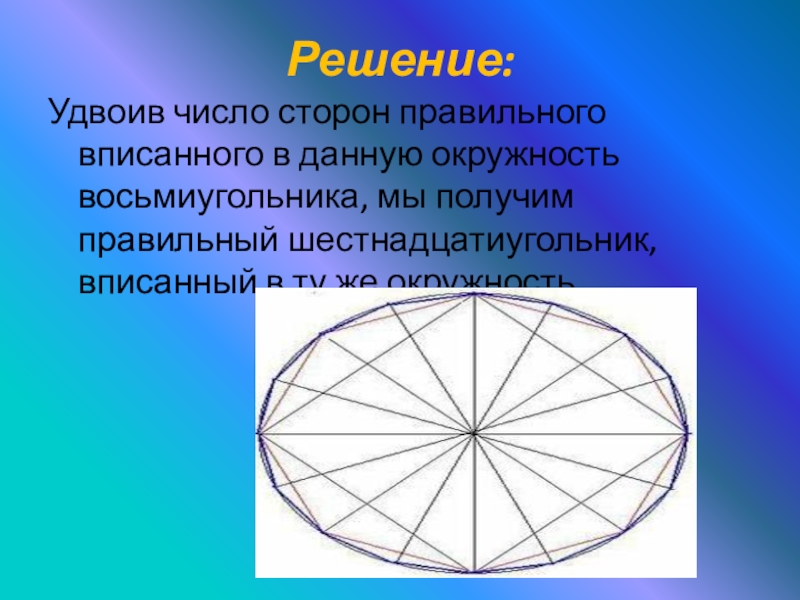
Слайд 23Решение:
Удвоив число сторон правильного вписанного в данную окружность восьмиугольника, мы получим
правильный шестнадцатиугольник, вписанный в ту же окружность