- Главная
- Разное
- Образование
- Спорт
- Естествознание
- Природоведение
- Религиоведение
- Французский язык
- Черчение
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, фоны, картинки для презентаций
- Экология
- Экономика
Презентация, доклад на тему Пирамида
Содержание
- 1. Пирамида
- 2. Введение.Значимость пирамиды в моем познании.Основная часть:1. Исторические
- 3. Исторические сведения о
- 4. Пирамидой называется многогранник, который состоит из плоского
- 5. Тетраэдр. S² =
- 6. Равногранный тетраэдр. 1.
- 7. Крыша имеет форму пирамиды с квадратным основанием
- 8. Построить сечение четырехугольной пирамиды плоскостью, проходящей через
- 9. Построить сечение четырехугольной пирамиды плоскостью, проходящей через
- 10. «Пирамида».
Слайд 2Введение.
Значимость пирамиды в моем познании.
Основная часть:
1. Исторические сведения о пирамиде.
2. Различные
3. Основные элементы.
4. Сечения пирамиды.
5. Виды пирамид:
правильная пирамида
усеченная пирамида
6. Площадь пирамиды.
7. Измерение объема.
8. Тетраэдр – простейшая пирамида:
основные элементы
виды тетраэдров
свойства тетраэдра
9. Задачи.
10. Решение задач.
Заключение.
Список использованной литературы.
Содержание:
Слайд 3Исторические сведения о
Египетские пирамиды – одно из семи чудес света. Что же такое пирамиды?
Усыпальницы египетских фараонов. Крупнейшие из них — пирамиды Хеопса, Хефрена и Микерина в Эль-Гизе в древности считались одним из Семи чудес света. Самая большая из трех — пирамида Хеопса (зодчий Хемиун, 27 в. до н. э.). Ее высота была изначально 147 м, а длина стороны основания — 232 м. Для ее сооружения потребовалось 2 млн. 300 тыс. огромных каменных блоков, средний вес которых 2,5 т. Плиты не скреплялись строительным раствором, лишь чрезвычайно точная подгонка удерживает их. В древности пирамиды были облицованы отполированными плитами белого известняка, вершины их были покрыты медными листами . В пирамиде Хеопса угол наклона таков, что высота пирамиды равна радиусу воображаемой окружности, в которую вписано основание пирамиды.
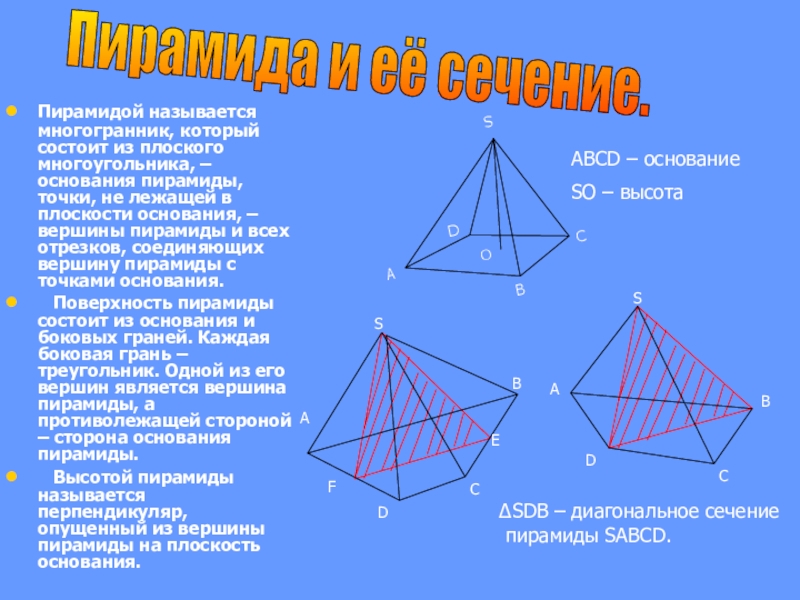
Слайд 4Пирамидой называется многогранник, который состоит из плоского многоугольника, – основания пирамиды,
Поверхность пирамиды состоит из основания и боковых граней. Каждая боковая грань – треугольник. Одной из его вершин является вершина пирамиды, а противолежащей стороной – сторона основания пирамиды.
Высотой пирамиды называется перпендикуляр, опущенный из вершины пирамиды на плоскость основания.
∆SDB – диагональное сечение
пирамиды SABCD.
Пирамида и её сечение.
ABCD – основание
SO – высота
Слайд 5
Тетраэдр.
S² = S1²+ S2²+ S3²
Ортоцентрический тетраэдр:
Прямоугольный тетраэдр:
Тетраэдр, в вершине которого сходятся три взаимно перпендикулярных ребра, называется прямоугольным.
Точка М и будет ортоцентром.
Тетраэдр является ортоцентрическим тогда и только тогда, когда его противоположные ребра перпендикулярны; или середины всех шести ребер лежат на одной сфере; или все ребра описанного параллелепипеда равны.
Слово «тетраэдр» оразовано из двух греческих слов: tetra – «четыре» и hedra – «основание, грань». Тетраэдр задается четырьмя вершинами; грани тетраэдра – четыре треугольника. В качестве основания может быть выбрана любая его грань.
Слайд 6
Равногранный тетраэдр.
1. описанный параллелепипед равногранного тетраэдра
2. у него имеется три оси симметрии (это общие перпендикуляры, проведенные к противоположным ребрам, они же бимедианы. Однако этих симметрий хватает, чтобы можно было совместить любые две указанные грани или вершины, но не ребра.
3. развертка тетраэдра, полученная при разрезании его по трем сходящимся в одной вершине ребрам, – треугольник ; этот треугольник должен быть остроугольным, потому что тупоугольный или прямоугольный при сгибании по соседним линиям не сложится в тетраэдр). Набор самосовмещений произвольного равногранного тетраэдра не так богат, как у правильного тетраэдра.
4. все трехгранные углы равны;
5. все медианы равны;
6. все высоты равны;
7. центры вписанной и описанной сфер и центроид совпадают;
8. радиусы описанных окружностей граней равны;
9. периметры граней равны;
10. площади граней равны
Свойства тетраэдра:
Слайд 7Крыша имеет форму пирамиды с квадратным основанием 4,5 м × 4,5
Решение задачи.
Дано: SABCD – Правильная четырехугольная пирамида. AB = BC = 4,5 м ∟SCO = 45˚; размеры листа:
70 см × 140 см; отходы 10%;
N = (Sбок + Sотх)/Sлиста
Найти: N
Решение:
Слайд 8Построить сечение четырехугольной пирамиды плоскостью, проходящей через прямую g и точку
1. Проведем прямую CD, CD ∩ g ≡ F,
F Є (SCD).
2. Проведем прямую FE, получим точки
пересечения с ребрами пирамиды:
SD ∩ FE ≡ H, SC ∩ FE ≡ G.
3. Построим прямую AD. AD ∩ g ≡ K, K Є (SAD).
4. Через точки K и H проведем прямую KH. KH ∩ SA ≡ L.
5. Построим прямую AВ, AВ ∩ g ≡ M, M Є (SAB).
6. Через точки M и L строим ML ∩ SB ≡ N.
7. Соединяем точки G, H, L, N. Сечение
GHLM построено.
Построение сечения.
Слайд 9Построить сечение четырехугольной пирамиды плоскостью, проходящей через прямую g и точку
1. Проведем прямую CD, CD ∩ g ≡ F,
F Є (SCD).
2. Проведем прямую FE, получим точки
пересечения с ребрами пирамиды:
SD ∩ FE ≡ H, SC ∩ FE ≡ G.
3. Построим прямую AD. AD ∩ g ≡ K, K Є (SAD).
4. Через точки K и H проведем прямую KH.
KH ∩ SA ≡ L.
5. Построим прямую AВ, AВ ∩ g ≡ M, M Є (SAB).
6. Через точки M и L строим ML ∩ SB ≡ N.
7. Соединяем точки G, H, L, N. Сечение
GHLM построено.
Построение сечения.