- Главная
- Разное
- Образование
- Спорт
- Естествознание
- Природоведение
- Религиоведение
- Французский язык
- Черчение
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, фоны, картинки для презентаций
- Экология
- Экономика
Презентация, доклад на тему Перпендикулярность прямых и плоскостей
Содержание
- 1. Перпендикулярность прямых и плоскостей
- 2. СодержаниеПерпендикулярные прямые в пространствеЛеммаОпределение прямой, перпендикулярной к
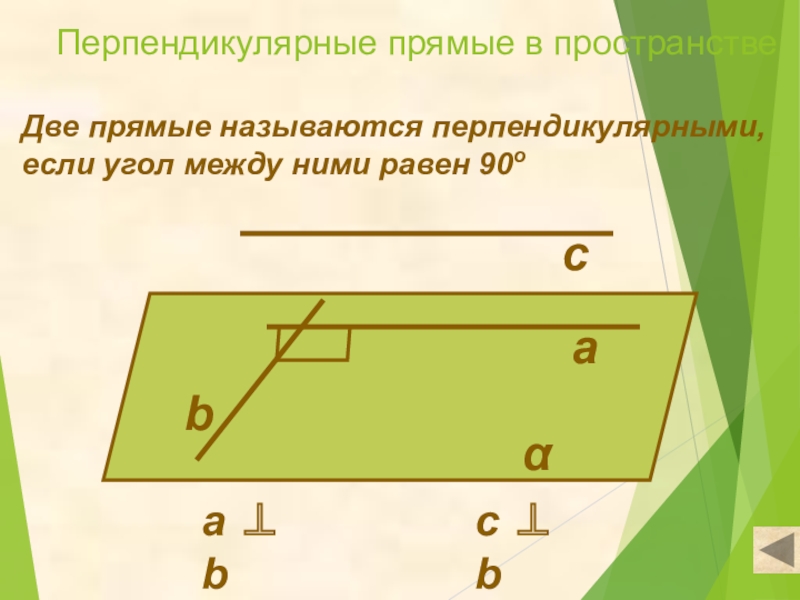
- 3. Перпендикулярные прямые в пространствеДве прямые называются перпендикулярными,если угол между ними равен 90оаbса ⊥ bc ⊥ bα
- 4. Лемма Если одна из двух параллельных прямых
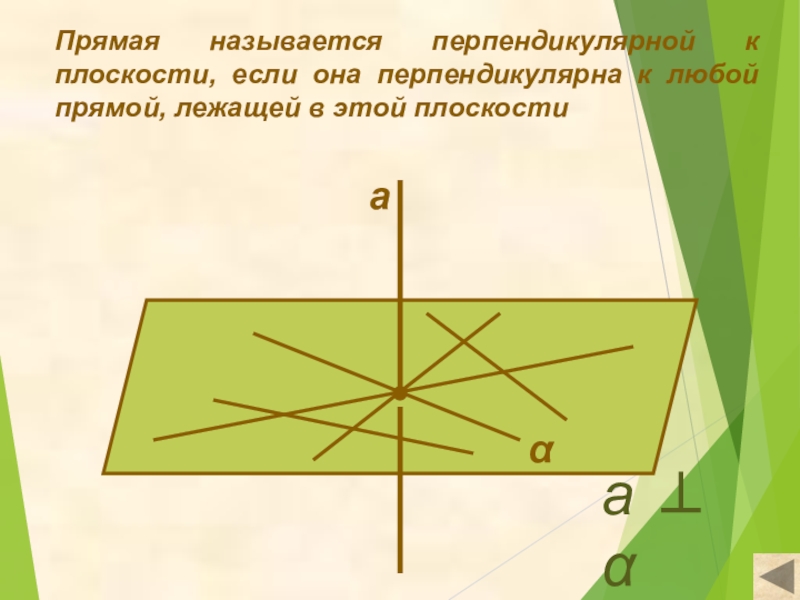
- 5. Прямая называется перпендикулярной к плоскости, если она
- 6. Теорема 1Если одна из двух параллельных прямых
- 7. Теорема 2 αДоказать: а || b
- 8. Признак перпендикулярности прямой и плоскостиЕсли прямая перпендикулярна
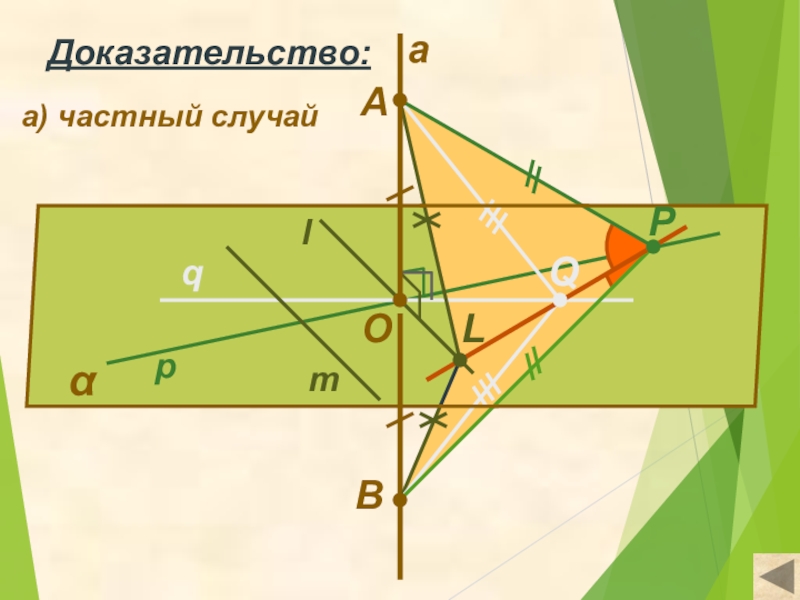
- 9. αqlmOapBPQДоказательство:Lа) частный случайA
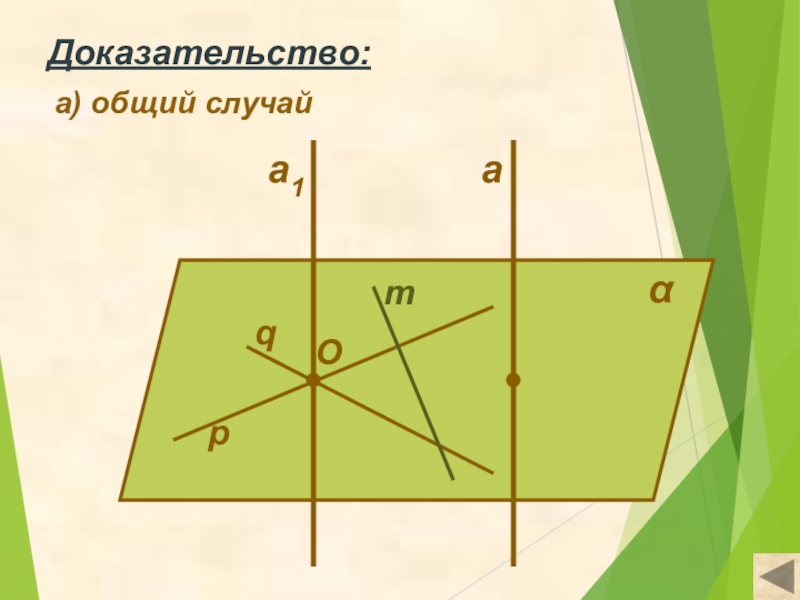
- 10. αqapmOДоказательство:а) общий случайa1
- 11. Теорема 4Через любую точку пространства проходит прямая,
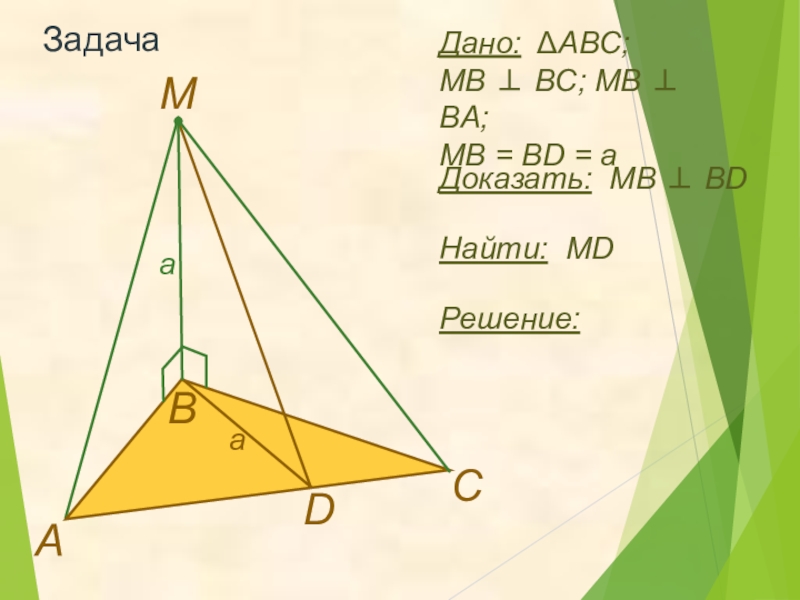
- 12. ЗадачаНайти: MDАВDMРешение:Дано: ΔABC; MB ⊥ BC; MB ⊥ BA;MB = BD = aДоказать: МB ⊥ BDCaa
- 13. Задача 128Доказать: OМ ⊥ (ABC)Дано: ABCD -
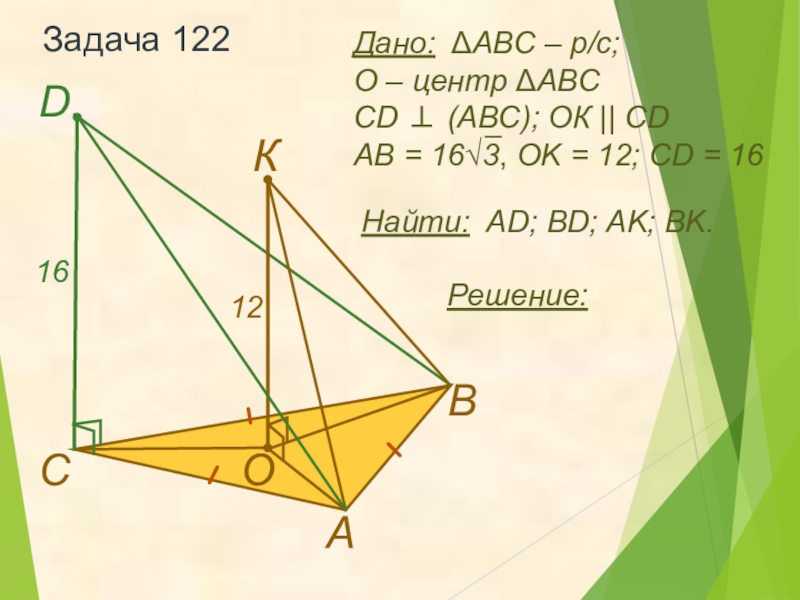
- 14. Задача 122Найти: AD; BD; AK; BK.АВDCOКРешение:1216
- 15. Перпендикуляр и наклонныеМАВНαМН ⊥ αА ∈ αВ
- 16. Теорема о трех перпендикулярахПрямая, проведенная в плоскости
- 17. Теорема, обратная теореме о трех перпендикулярахПрямая, проведенная
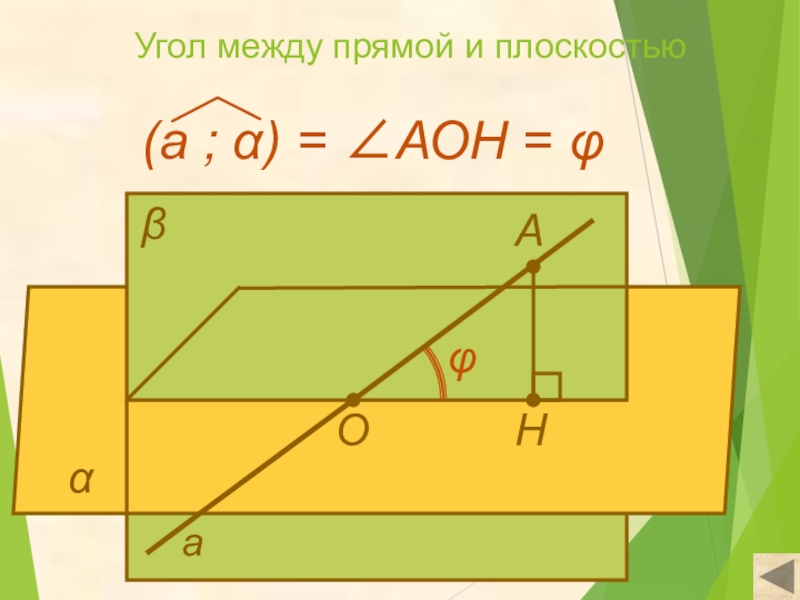
- 18. Угол между прямой и плоскостьюАНαβаОφ
Слайд 2Содержание
Перпендикулярные прямые в пространстве
Лемма
Определение прямой, перпендикулярной к плоскости
Теорема о перпендикулярности двух
Теорема о параллельности двух перпендикулярных прямых к плоскости
Признак перпендикулярности прямой и плоскости
Теорема о существовании и единственности прямой, перпендикулярной к данной плоскости
Перпендикуляр и наклонные
Теорема о трех перпендикулярах
Теорема, обратная теореме о трех перпендикулярах
Угол между прямой и плоскостью
Слайд 3Перпендикулярные прямые в пространстве
Две прямые называются перпендикулярными,
если угол между ними равен
а
b
с
а ⊥ b
c ⊥ b
α
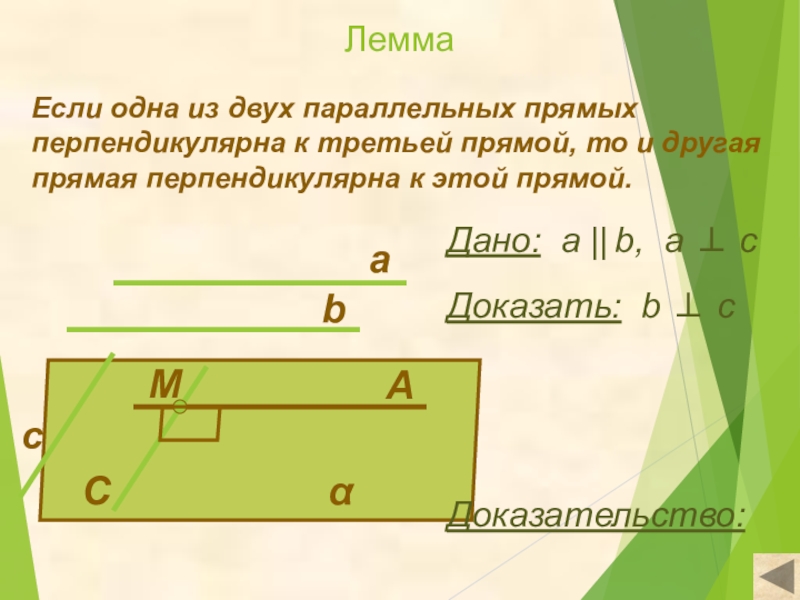
Слайд 4Лемма
Если одна из двух параллельных прямых перпендикулярна к третьей прямой,
A
C
a
α
M
b
c
Дано: а || b, a ⊥ c
Доказать: b ⊥ c
Доказательство:
Слайд 5Прямая называется перпендикулярной к плоскости, если она перпендикулярна к любой прямой,
α
а
а ⊥ α
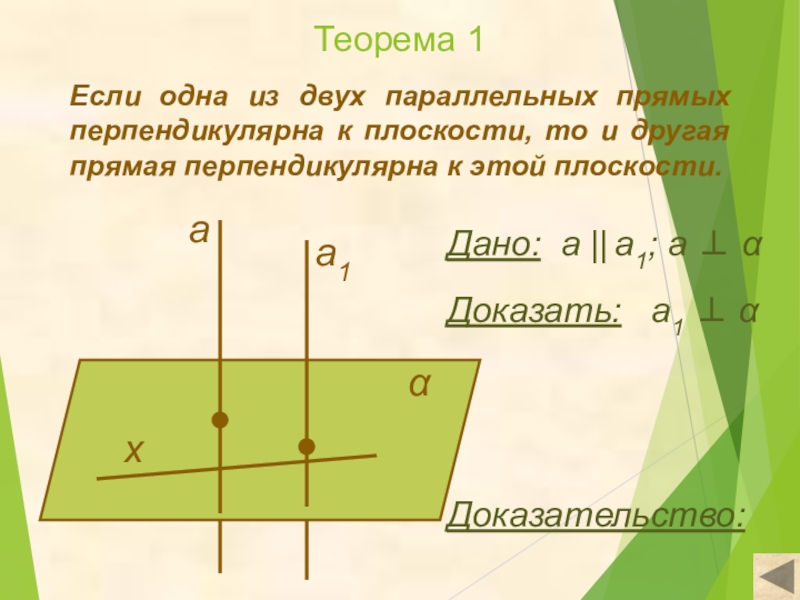
Слайд 6Теорема 1
Если одна из двух параллельных прямых перпендикулярна к плоскости, то
α
х
Дано: а || а1; a ⊥ α
Доказать: а1 ⊥ α
Доказательство:
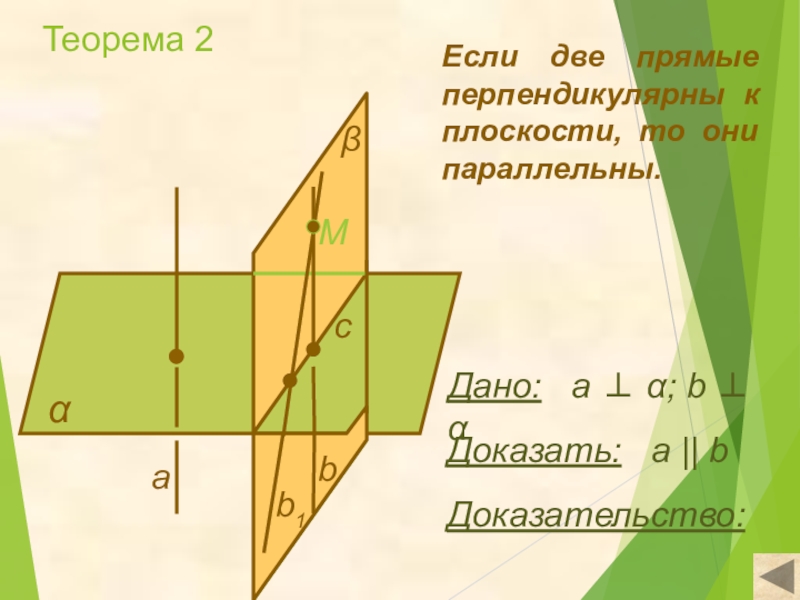
Слайд 7Теорема 2
α
Доказать: а || b
Доказательство:
Если две прямые перпендикулярны
Дано: а ⊥ α; b ⊥ α
M
с
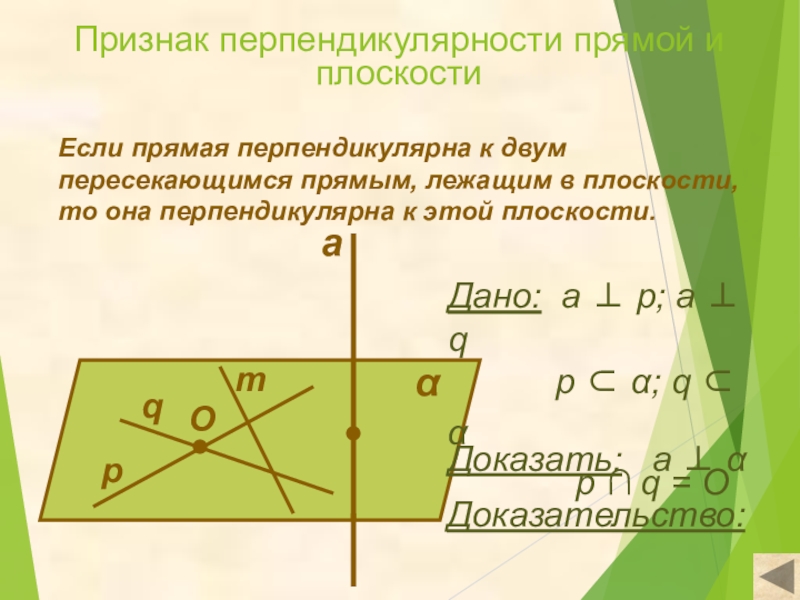
Слайд 8Признак перпендикулярности прямой и плоскости
Если прямая перпендикулярна к двум пересекающимся прямым,
то она перпендикулярна к этой плоскости.
α
q
Доказать: а ⊥ α
Доказательство:
p
m
O
Дано: а ⊥ p; a ⊥ q
p ⊂ α; q ⊂ α
p ∩ q = O
Слайд 11
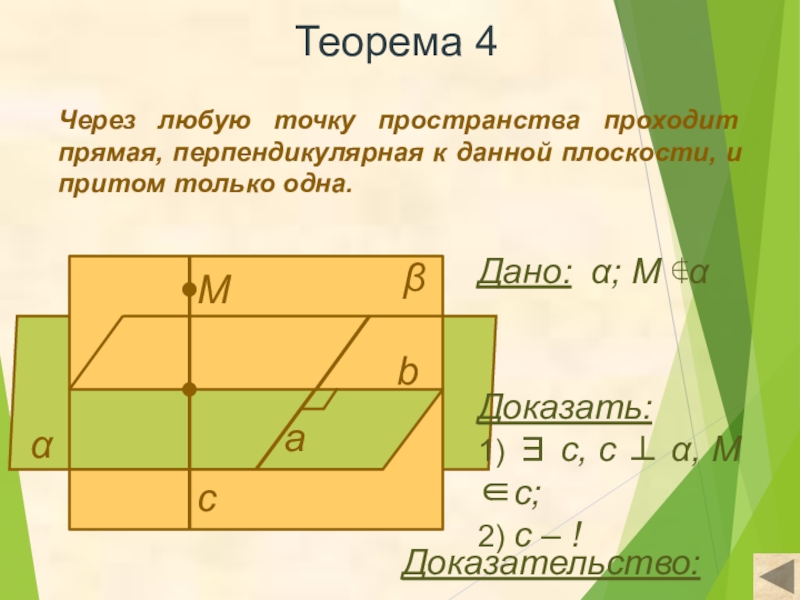
Теорема 4
Через любую точку пространства проходит прямая, перпендикулярная к данной плоскости,
α
а
М
b
с
Доказать:
1) ∃ с, с ⊥ α, М ∈с;
2) с – !
Доказательство:
Дано: α; М ∉α
Слайд 13
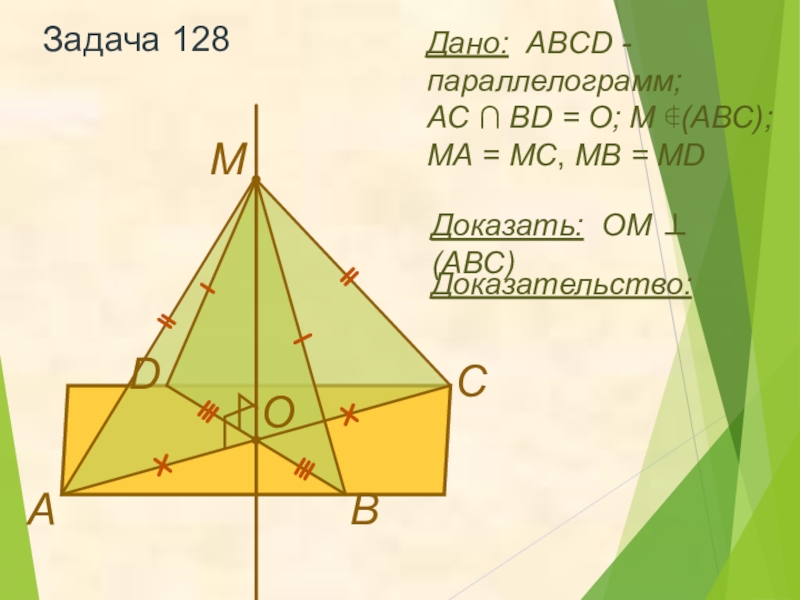
Задача 128
Доказать: OМ ⊥ (ABC)
Дано: ABCD - параллелограмм;
AC ∩ BD
МА = МС, MB = MD
А
В
D
C
O
М
Доказательство:
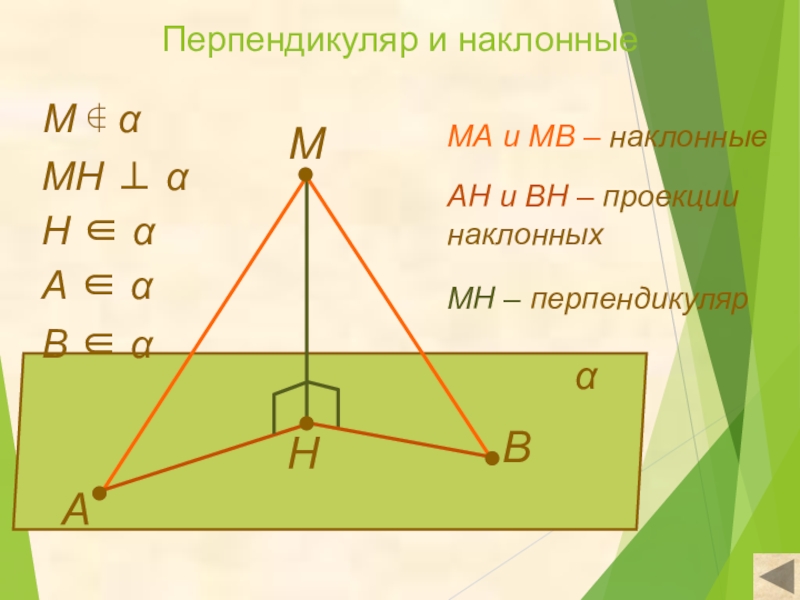
Слайд 15Перпендикуляр и наклонные
М
А
В
Н
α
МН ⊥ α
А ∈ α
В ∈ α
МА и МВ
Н ∈ α
АН и ВН – проекции
наклонных
МН – перпендикуляр
М ∉ α
Слайд 16
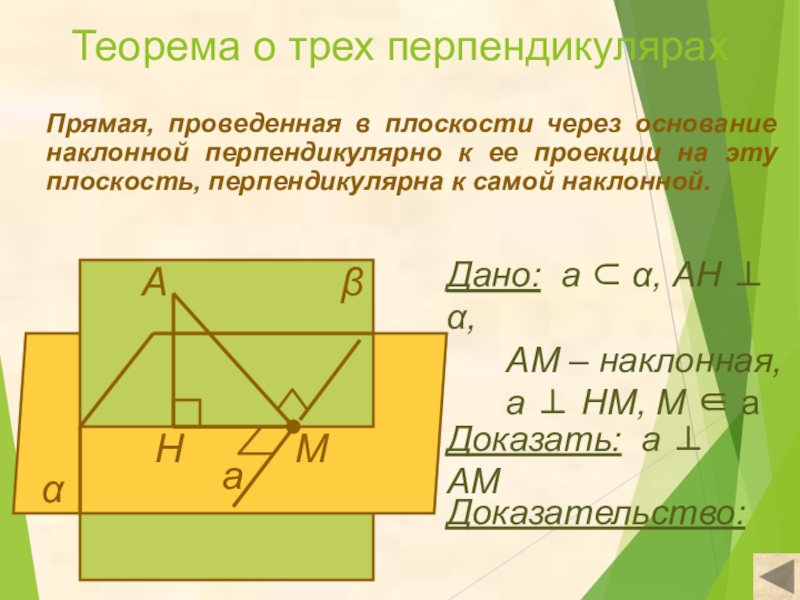
Теорема о трех перпендикулярах
Прямая, проведенная в плоскости через основание наклонной перпендикулярно
А
Н
М
α
β
а
Дано: а ⊂ α, АН ⊥ α,
АМ – наклонная,
а ⊥ НМ, М ∈ а
Доказать: а ⊥ АМ
Доказательство:
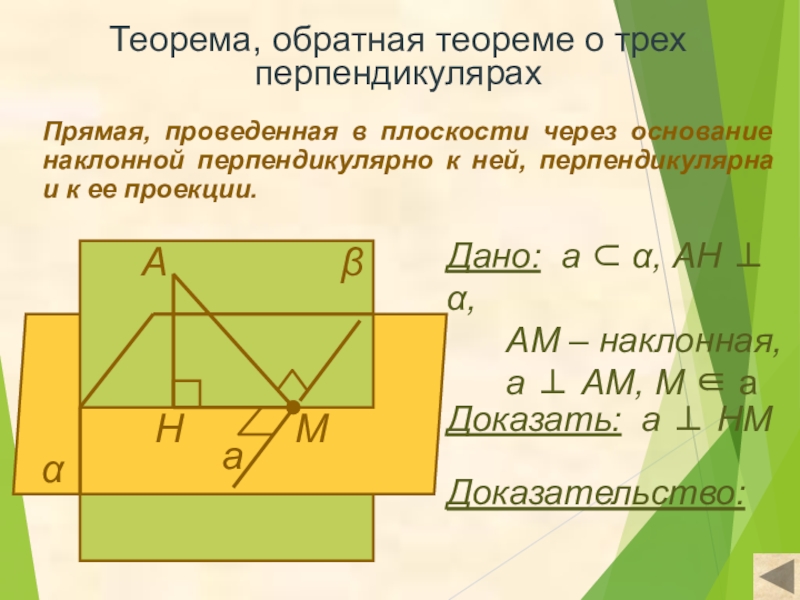
Слайд 17Теорема, обратная теореме о трех перпендикулярах
Прямая, проведенная в плоскости через основание
А
Н
М
α
β
а
Дано: а ⊂ α, АН ⊥ α,
АМ – наклонная,
а ⊥ АМ, М ∈ а
Доказать: а ⊥ НМ
Доказательство: