- Главная
- Разное
- Образование
- Спорт
- Естествознание
- Природоведение
- Религиоведение
- Французский язык
- Черчение
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, фоны, картинки для презентаций
- Экология
- Экономика
Презентация, доклад на тему Открытый урок по геометрии в 8 классе Теорема Пифагора
Содержание
- 1. Открытый урок по геометрии в 8 классе Теорема Пифагора
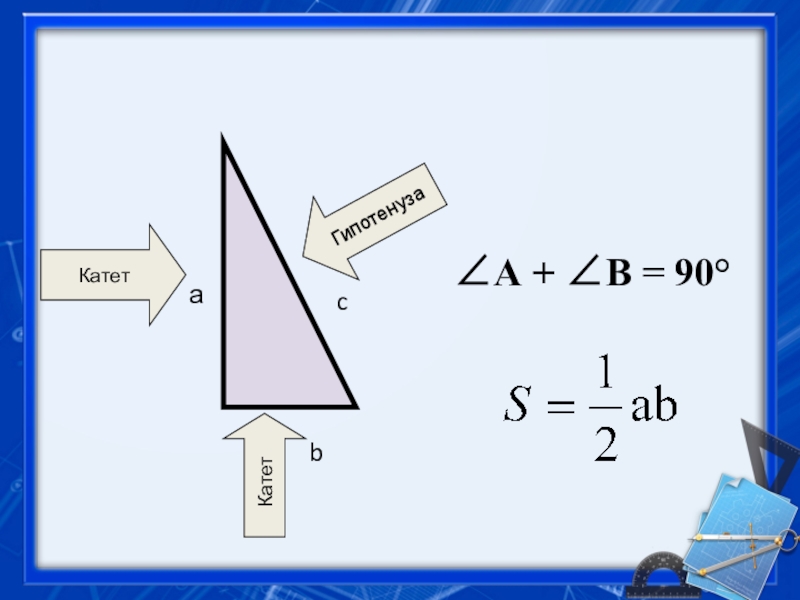
- 2. аcbКатетКатетГипотенузаА + В = 90°
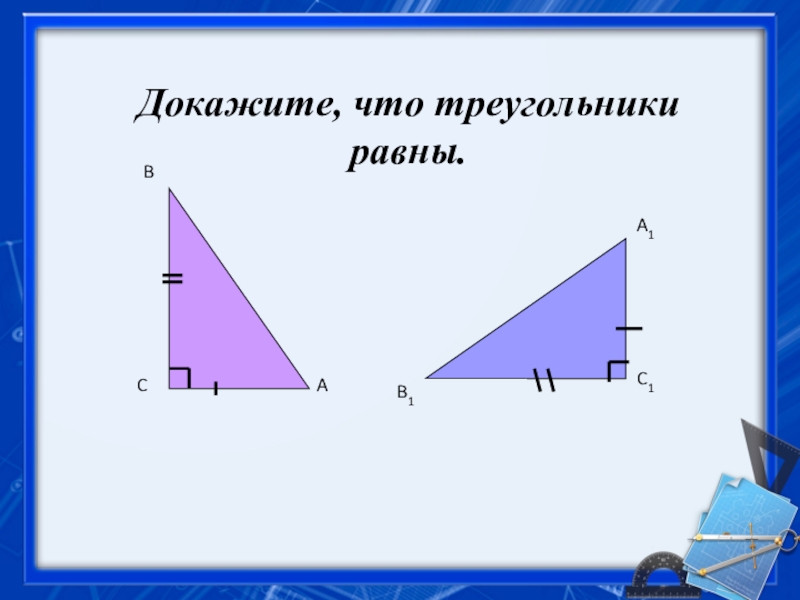
- 3. Докажите, что треугольники равны.
- 4. Свойства площадей Равные многоугольники имеют равные площади.F = H S1 = S2S1S2
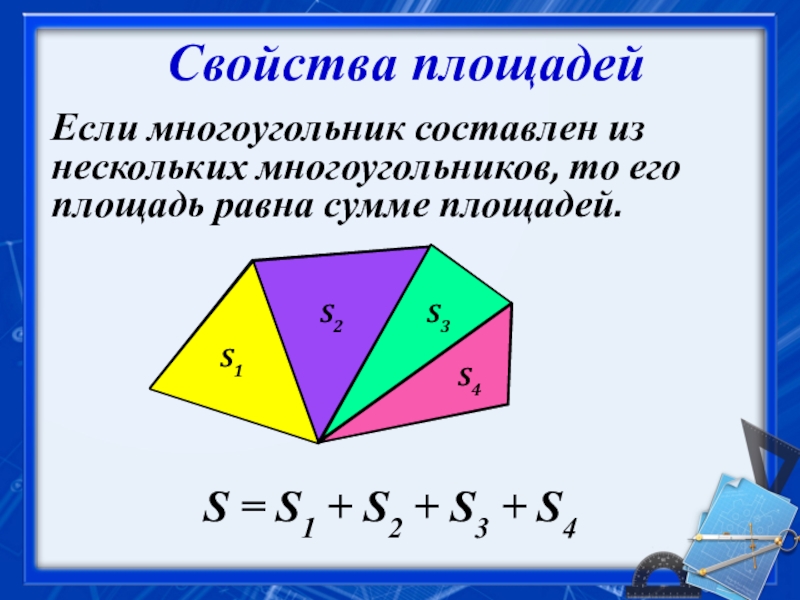
- 5. Свойства площадей Если многоугольник составлен изнескольких многоугольников,
- 6. Свойства площадей Площадь квадрата равна квадрату его стороны.
- 7. Найти 3, если 1+ 2 = 90°.
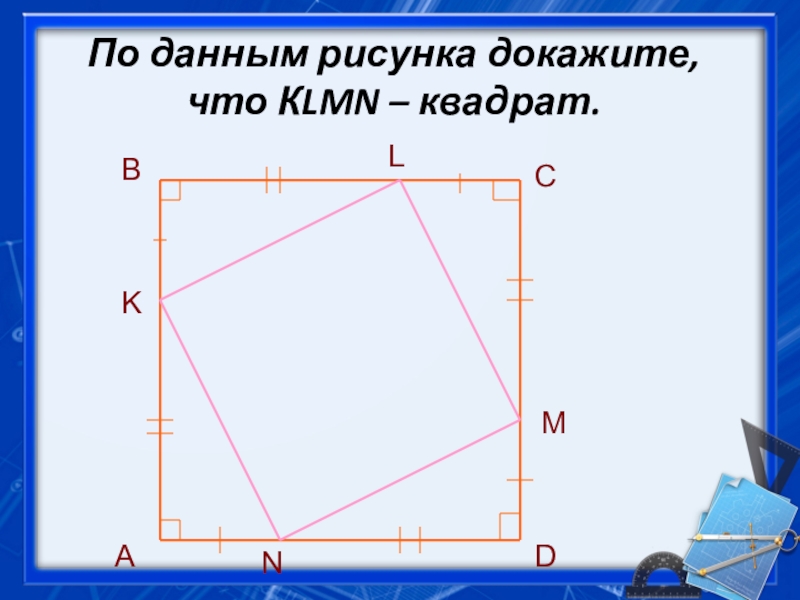
- 8. По данным рисунка докажите, что КLMN – квадрат. BCD А KL MN
- 9. Ребята увидели на дереве маленького котенка. Котенок
- 10. «Теорема Пифагора» «Пребудет вечной истина, как скоро
- 11. «Геометрия владеет двумя сокровищами: одно из них
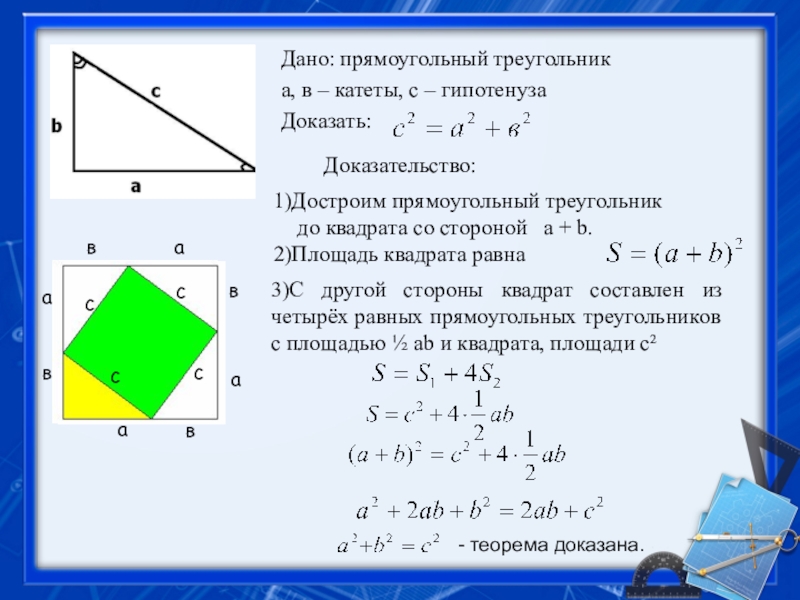
- 12. Дано: прямоугольный треугольника, в – катеты, с
- 13. История о Пифагоре:Пифагор родился в 580 г.
- 14. Пифагор перебрался в г. Милеет и стал
- 15. Важные открытия, связанные с именем Пифагора:в географии
- 16. Интересное о Пифагоре:Пифагор – это на самом
- 17. История теоремы: Изучение вавилонских
- 18. Теорему называли «мостом ослов», так как слабые
- 19. Из-за чертежей, сопровождающих теорему Пифагора, учащиеся называли
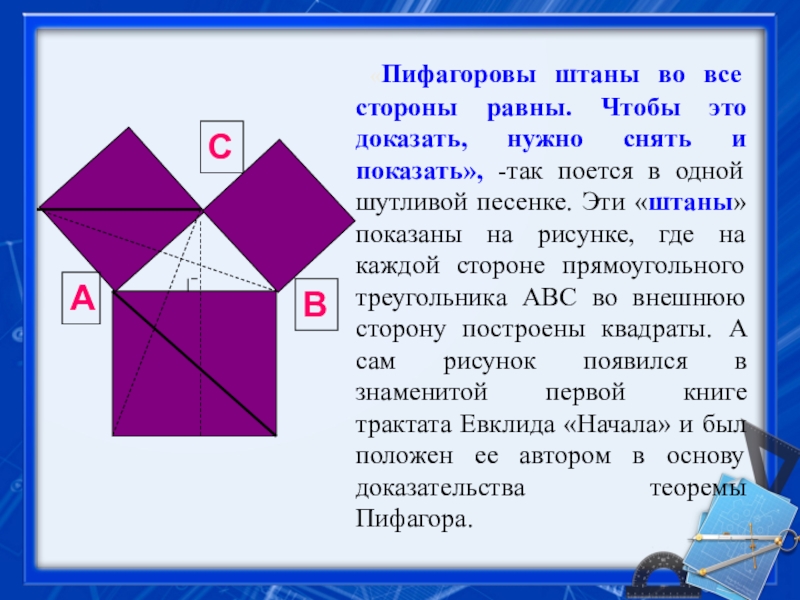
- 20. «Пифагоровы штаны во все стороны равны.
- 21. Пифагоровы штаны
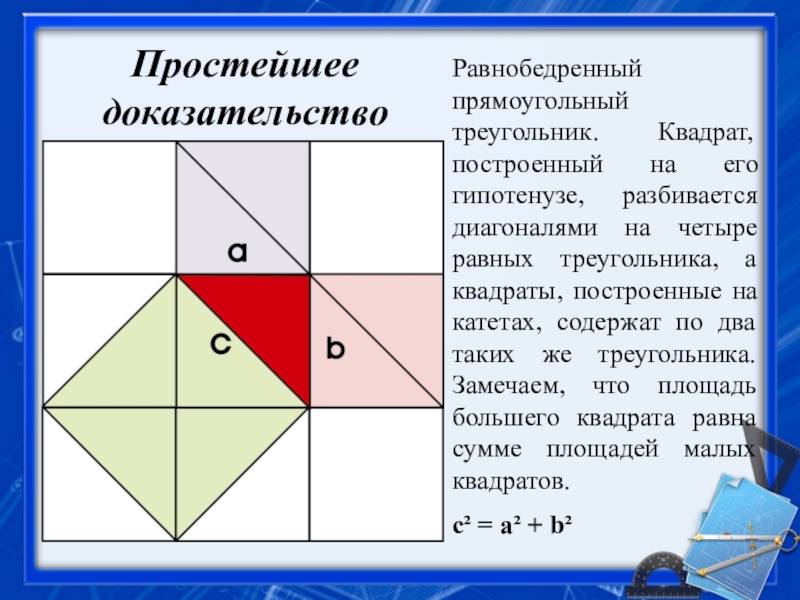
- 22. Равнобедренный прямоугольный треугольник. Квадрат, построенный на его
- 23. Слайд 23
- 24. В некоторых списках «Начал» Евклида теорема Пифагора
- 25. На данный момент в научной литературе зафиксировано
- 26. Алгоритм решения задач по теореме Пифагора Внимательно
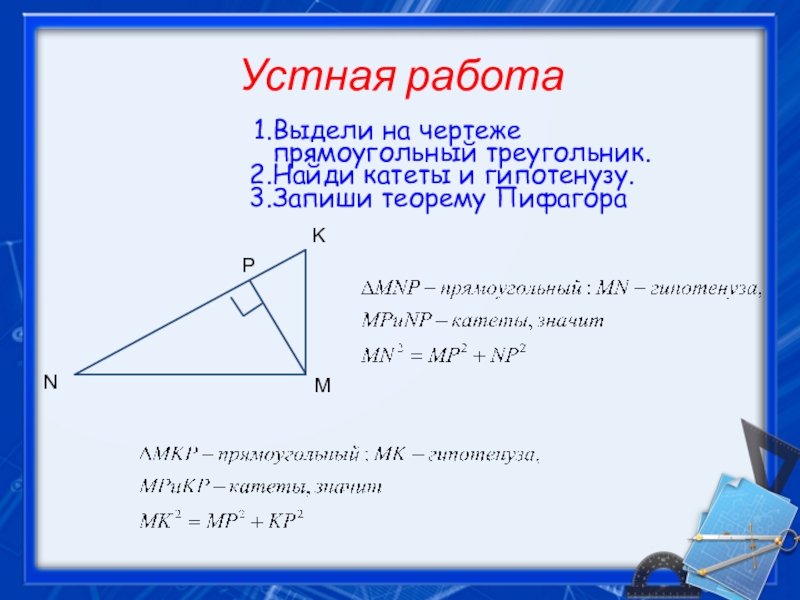
- 27. Устная работа Выдели на чертеже прямоугольный треугольник. Найди катеты и гипотенузу. Запиши теорему Пифагора
- 28. Устная работа Выдели на чертеже прямоугольный треугольник. Найди катеты и гипотенузу. Запиши теорему Пифагора
- 29. Устная работа Выдели на чертеже прямоугольный треугольник. Найди катеты и гипотенузу. Запиши теорему Пифагора
- 30. Дано: ∆ АВС, ےВ = 900, АВ = 8 м,
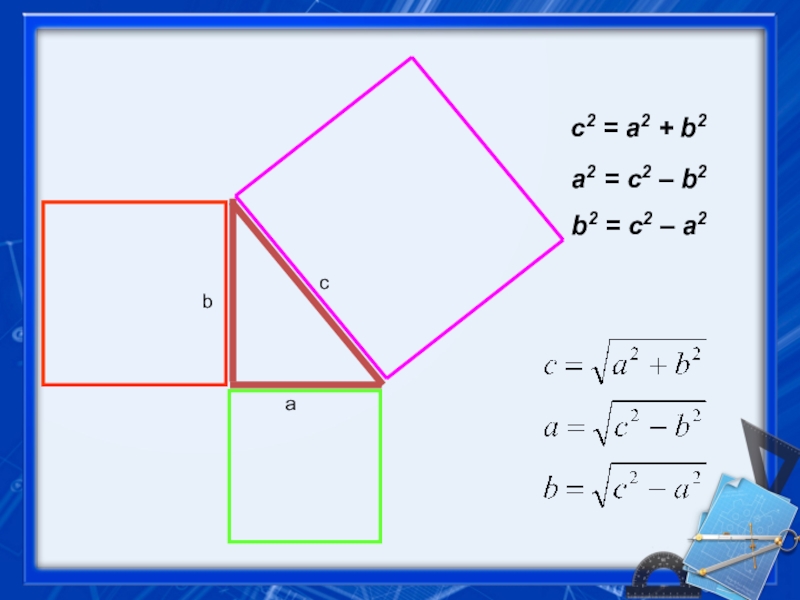
- 31. aba2 = c2 – b2b2 = c2 – a2c2 = a2 + b2
- 32. Решение задач Найти неизвестную сторону треугольника
- 33. Случай из следственной практики. Получив
- 34. 124см180 см?с= Очевидно,
- 35. Решение задач
- 36. Слайд 36
- 37. Домашнее заданиеП.54, задачи 483 (в), 484 (б, г, ), 486 (б).Подготовить сообщение «Египетский треугольник».
аcbКатетКатетГипотенузаА + В = 90°
Слайд 5Свойства площадей
Если многоугольник составлен из
нескольких многоугольников, то его
площадь равна сумме
площадей.
S1
S2
S3
S4
S = S1 + S2 + S3 + S4
Слайд 9Ребята увидели на дереве маленького котенка. Котенок жалобно пищал и звал
на помощь. Но вот беда: ребята могут приблизить свою лестницу к дереву не ближе, чем на 6м, высота дерева – 8м. Свою лестницу ребята могут растянуть не более, чем на 11м. Достаточно ли этого, чтобы помочь бедному котенку?
Слайд 10«Теорема Пифагора»
«Пребудет вечной истина, как скоро
Ее познает слабый
человек!
И ныне теорема Пифагора
Верна, как и в его далекий век.»
И ныне теорема Пифагора
Верна, как и в его далекий век.»
сонет Шамиссо
Слайд 11«Геометрия владеет двумя сокровищами: одно из них - это теорема Пифагора,
а другое - деление отрезка в среднем и крайнем отношении… Первое можно сравнить с мерой золота; второе же больше напоминает драгоценный камень.»
Иоганн Кеплер
Иоганн Кеплер
Слайд 12Дано: прямоугольный треугольник
а, в – катеты, с – гипотенуза
Доказать:
Доказательство:
- теорема
доказана.
1)Достроим прямоугольный треугольник до квадрата со стороной a + b.
2)Площадь квадрата равна
3)С другой стороны квадрат составлен из четырёх равных прямоугольных треугольников с площадью ½ аb и квадрата, площади с²
а
в
а
а
а
в
в
в
c
c
c
c
Слайд 13История о Пифагоре:
Пифагор родился в 580 г. до н.э. в Древней
Греции на острове Самос, который находится в Эгейском море, поэтому его называют Пифагором Самосским.
Его отец был резчиком по камню. Ещё в детстве Пифагор проявлял незаурядные способности, и когда подрос, воображению юноши стало тесно на маленьком острове.
Его отец был резчиком по камню. Ещё в детстве Пифагор проявлял незаурядные способности, и когда подрос, воображению юноши стало тесно на маленьком острове.
Слайд 14Пифагор перебрался в г. Милеет и стал учеником Фалеса, которому в
то время шёл восьмой десяток. Мудрый учёный посоветовал юноше отправиться в Египет. Когда Пифагор постиг науку египетских жрецов, то отправился домой, чтобы там создать свою школу.
Пифагорейцы, как их позднее стали называть, занимались математикой, философией, естественными науками.
Пифагорейцы, как их позднее стали называть, занимались математикой, философией, естественными науками.
Слайд 15Важные открытия, связанные с именем Пифагора:
в географии и астрономии – представление
о том, что Земля – шар и что существуют другие, похожие на неё миры;
в музыке – зависимость между длиной струны арфы и звуком, который она издаёт;
в геометрии – построение правильных многоугольников (один из них пятиконечная звезда – стал символом пифагорейцев).
в музыке – зависимость между длиной струны арфы и звуком, который она издаёт;
в геометрии – построение правильных многоугольников (один из них пятиконечная звезда – стал символом пифагорейцев).
Слайд 16Интересное о Пифагоре:
Пифагор – это на самом деле прозвище, а не
имя (Пифагор - "убеждающий речью").
Увлекался спортом, побеждал в кулачном бою на Олимпийских играх.
Придумал специальную кружку, которая заставляла пить только в ограниченных количествах. Сегодня она продается на Родосе, Самосе и Крите как сувенир.
Пифагор считал, что нельзя употреблять пищу животного происхождения. Он верил, что в животных переселяются души людей.
Увлекался спортом, побеждал в кулачном бою на Олимпийских играх.
Придумал специальную кружку, которая заставляла пить только в ограниченных количествах. Сегодня она продается на Родосе, Самосе и Крите как сувенир.
Пифагор считал, что нельзя употреблять пищу животного происхождения. Он верил, что в животных переселяются души людей.
Слайд 17История теоремы:
Изучение вавилонских клинописных таблиц и древних
китайских рукописей показало, что это утверждение было известно задолго до Пифагора. Заслуга же Пифагора состояла в том, что он открыл доказательство этой теоремы.
Согласно одной из легенд, знаменитую теорему Пифагор добыл как выигрыш с неизвестным математиком. Тот отдал свиток с теоремой Пифагору и сказал, что человек, который владеет этим свитком, будет известным не одно тысячелетие…
Согласно одной из легенд, знаменитую теорему Пифагор добыл как выигрыш с неизвестным математиком. Тот отдал свиток с теоремой Пифагору и сказал, что человек, который владеет этим свитком, будет известным не одно тысячелетие…
Слайд 18Теорему называли «мостом ослов», так как слабые ученики, заучивающие теоремы наизусть,
без понимания, и прозванные поэтому «ослами», были не в состоянии преодолеть теорему Пифагора, служившую для них вроде непреодолимого моста.
Слайд 19Из-за чертежей, сопровождающих теорему Пифагора, учащиеся называли ее так же “ветряной
мельницей”, составляли стихи вроде “Пифагоровы штаны на все стороны равны”, рисовали карикатуры.
Слайд 20 «Пифагоровы штаны во все стороны равны. Чтобы это доказать, нужно
снять и показать», -так поется в одной шутливой песенке. Эти «штаны» показаны на рисунке, где на каждой стороне прямоугольного треугольника АВС во внешнюю сторону построены квадраты. А сам рисунок появился в знаменитой первой книге трактата Евклида «Начала» и был положен ее автором в основу доказательства теоремы Пифагора.
Слайд 22Равнобедренный прямоугольный треугольник. Квадрат, построенный на его гипотенузе, разбивается диагоналями на
четыре равных треугольника, а квадраты, построенные на катетах, содержат по два таких же треугольника. Замечаем, что площадь большего квадрата равна сумме площадей малых квадратов.
с² = a² + b²
с² = a² + b²
Простейшее доказательство
Слайд 24В некоторых списках «Начал» Евклида теорема Пифагора называлась теоремой Нимфы, «теорема
– бабочка», по-видимому из-за сходства чертежа с бабочкой, поскольку словом «нимфа» греки называли бабочек. Нимфами греки называли еще и невест, а также некоторых богинь.
При переводе с греческого арабский переводчик, вероятно, не обратил внимания на чертеж и перевел слово «нимфа» не как «бабочка», а как «невеста». Так и появилось ласковое название знаменитой теоремы – «Теорема Невесты».
Слайд 25На данный момент в научной литературе зафиксировано 367 доказательств теоремы Пифагора.
Именно это число и занесено в книгу рекордов Гиннеса, а сама теорема считается имеющей наибольшее количество доказательств.
Слайд 26Алгоритм решения задач по теореме Пифагора
Внимательно прочти задачу, разберись с
условием.
По условию сделай чертеж.
Выдели на чертеже прямоугольный треугольник.
Найди катеты и гипотенузу.
Запиши теорему Пифагора и соотнеси данные в задаче с ней.
Выполни подстановку данных.
Соотнеси полученный ответ с вопросом задачи и смыслом условия.
По условию сделай чертеж.
Выдели на чертеже прямоугольный треугольник.
Найди катеты и гипотенузу.
Запиши теорему Пифагора и соотнеси данные в задаче с ней.
Выполни подстановку данных.
Соотнеси полученный ответ с вопросом задачи и смыслом условия.
Слайд 27Устная работа
Выдели на чертеже прямоугольный треугольник.
Найди катеты и гипотенузу.
Запиши
теорему Пифагора
Слайд 28Устная работа
Выдели на чертеже прямоугольный треугольник.
Найди катеты и гипотенузу.
Запиши
теорему Пифагора
Слайд 29Устная работа
Выдели на чертеже прямоугольный треугольник.
Найди катеты и гипотенузу.
Запиши
теорему Пифагора
Слайд 30Дано: ∆ АВС, ےВ = 900, АВ = 8 м,
ВС = 6 м
Найти: АС
Решение: Δ АВС – прямоугольный
По теореме Пифагора АС2=АВ2+ВС2 ═>
АС2= 82+62 – это математическая модель данной ситуации.
АС2 = 100, АС = 10
Ответ: 10 м до котенка, т.е. лестницы вполне достаточно.
А
С
В
Слайд 33Случай из следственной практики.
Получив сообщение о краже, следователь
выехал на место происшествия. Заявитель утверждал, что преступник проник в помещение, где хранились ценности, через окно. Осмотр показал, что подоконник находится на расстоянии 124 см от
земли, поверхность земли на расстоянии 180 см от стены покрыта густой порослью, не имеющей никаких следов повреждений.
Возникло предположение, что преступник проник в помещение через окно, каким-то образом преодолел расстояние между наружным краем поросли и подоконником.
Оно было определено с применением теоремы Пифагора.
Слайд 34124см
180 см
?
с=
Очевидно, что преодолеть такое расстояние
без какого-либо средства, например, лестницы, невозможно. Поиски этого средства не увенчались успехом.
С учётом этого обстоятельства и некоторых других данных, следователь выдвинул версию об инсценировке кражи, которая в ходе дальнейшего расследования подтвердилась.
Так школьная геометрия помогла следствию.
С учётом этого обстоятельства и некоторых других данных, следователь выдвинул версию об инсценировке кражи, которая в ходе дальнейшего расследования подтвердилась.
Так школьная геометрия помогла следствию.
Решение
=
≈ 219 см.
с
Слайд 37Домашнее задание
П.54, задачи 483 (в), 484 (б, г, ), 486 (б).
Подготовить
сообщение «Египетский треугольник».
