- Главная
- Разное
- Образование
- Спорт
- Естествознание
- Природоведение
- Религиоведение
- Французский язык
- Черчение
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, фоны, картинки для презентаций
- Экология
- Экономика
Презентация, доклад на тему Медианы, высоты, биссектрисы. первый признак равенства треугольников
Содержание
- 1. Медианы, высоты, биссектрисы. первый признак равенства треугольников
- 2. № 1Дано: МРС = DAB
- 3. № 1a) DB = 8 см, AB = 12 см812730Какое из высказываний верно?
- 4. № 1б) АВ = 8 см, М = 730812730Какое из высказываний верно?
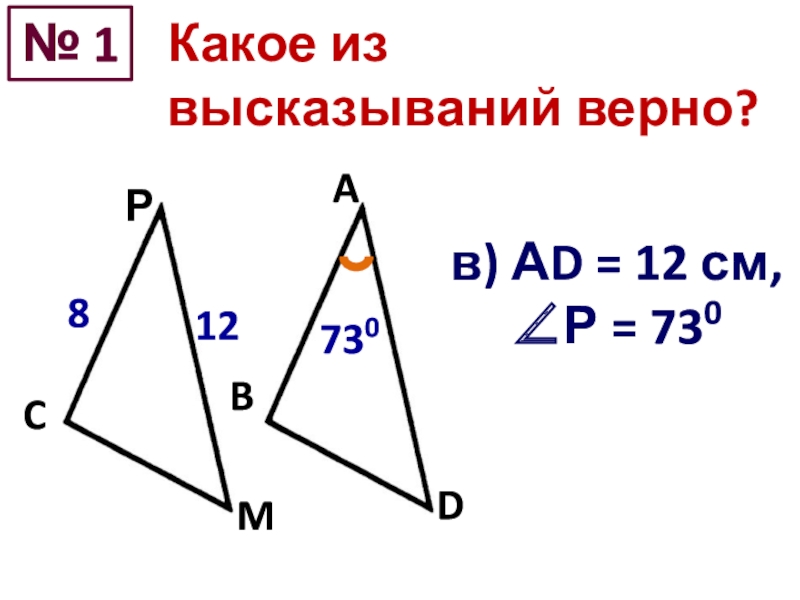
- 5. № 1в) АD = 12 см, Р = 730812730Какое из высказываний верно?
- 6. № 1г) АВ = 12 см, Р = 730812730Какое из высказываний верно?
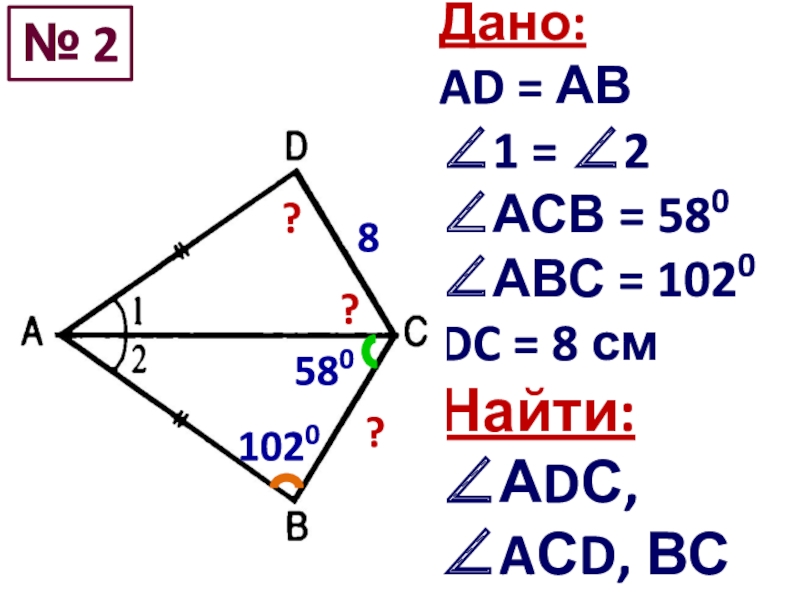
- 7. Дано: AD = АВ1 = 2АСВ =
- 8. Дано: ВС = АD, 1 = 2АСD
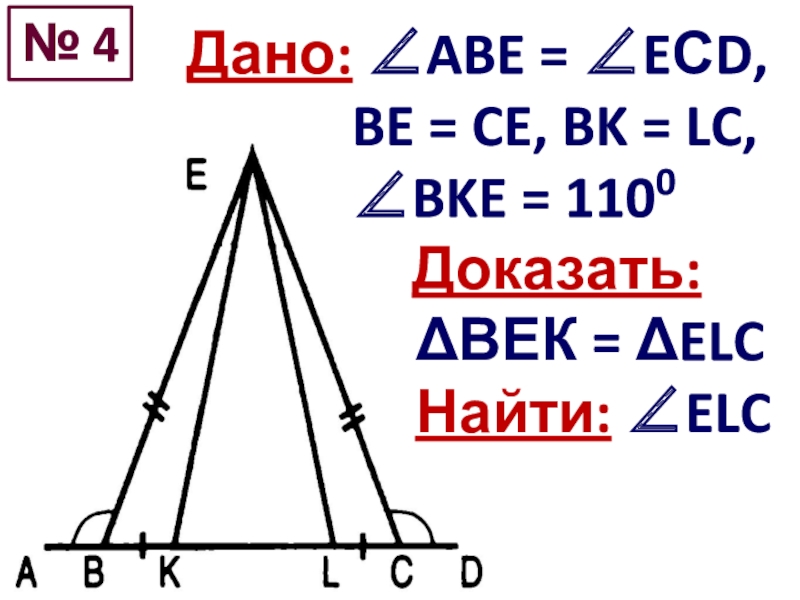
- 9. Дано: ABE = EСD, BE = CE,
- 10. Медианы, биссектрисы и высоты треугольника
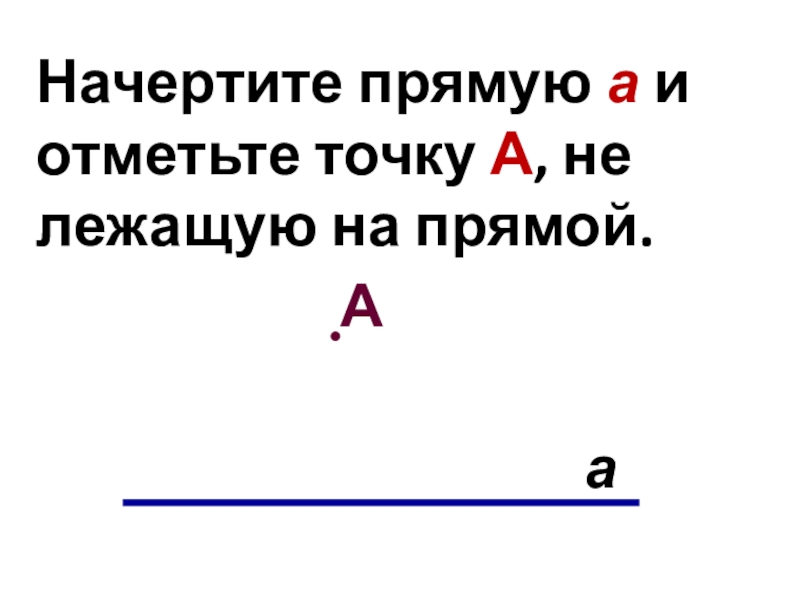
- 11. Начертите прямую а и отметьте точку А, не лежащую на прямой.аА
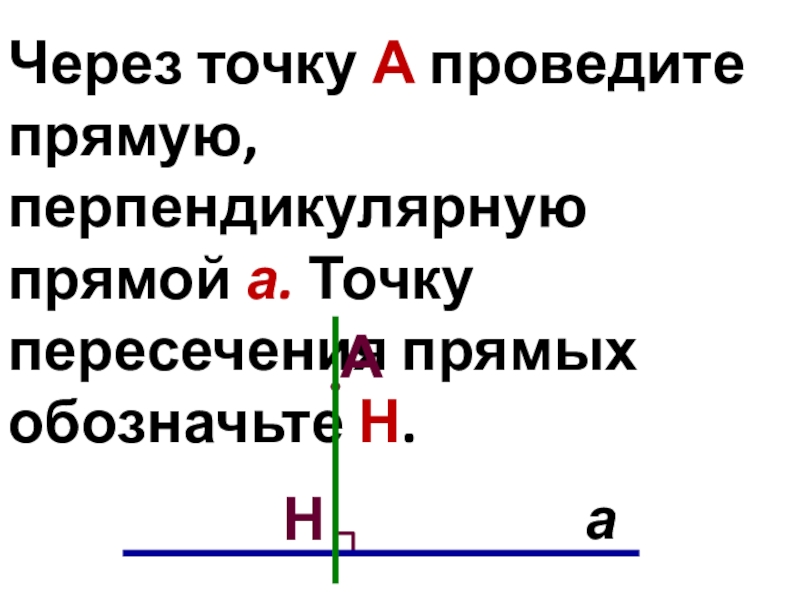
- 12. Через точку А проведите прямую, перпендикулярную прямой а. Точку пересечения прямых обозначьте Н.аАН
- 13. Отрезок АН – перпендикуляр, проведённый из точки А к прямой а, если: АН а;Аа, На
- 14. АН а;Аа, НаТочка Н – основание перпендикуляра
- 15. Теорема. Из точки, не лежащей на прямой,
- 16. Отрезок, соединяющий вершину треугольника с серединой противоположной стороны, называется медианой треугольника
- 17. СВАВМ – медиана АВС, если АМ = МС, где МАСМЛюбой треугольник имеет три медианы
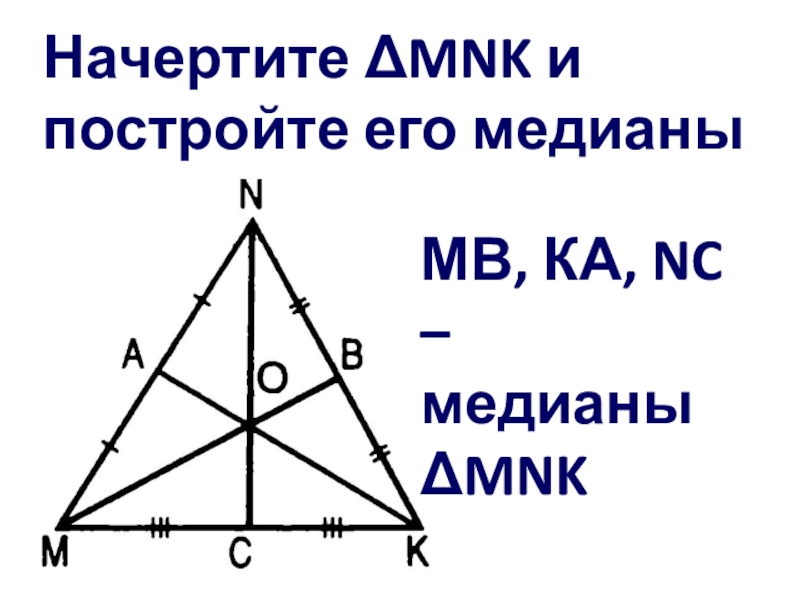
- 18. Начертите MNK и постройте его медианыМВ, КА, NC – медианыMNK
- 19. МВ, КА, NC – медианыMNK МВКАNC = О
- 20. Отрезок биссектрисы угла треугольника, соединяющий вершину треугольника с точкой противоположной стороны, называется биссектрисой треугольника
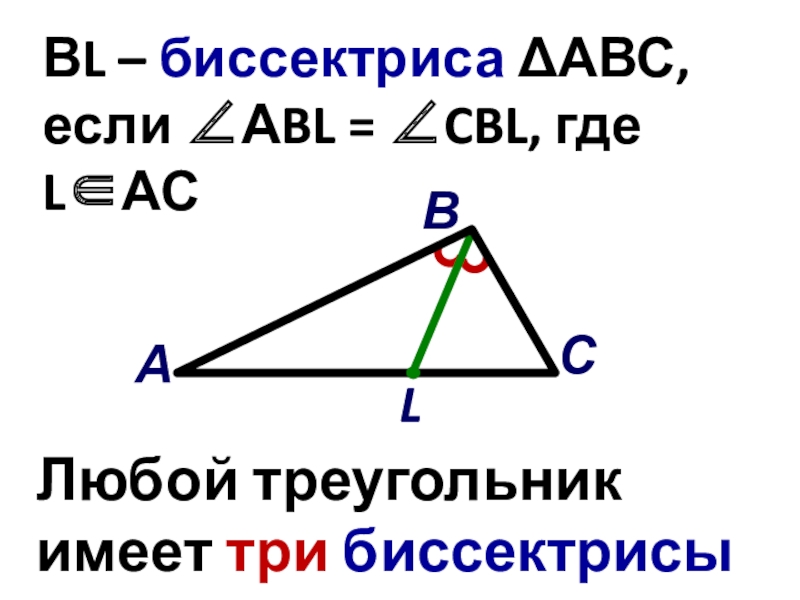
- 21. СВАВL – биссектриса АВС, если АBL = CBL, где LАСLЛюбой треугольник имеет три биссектрисы
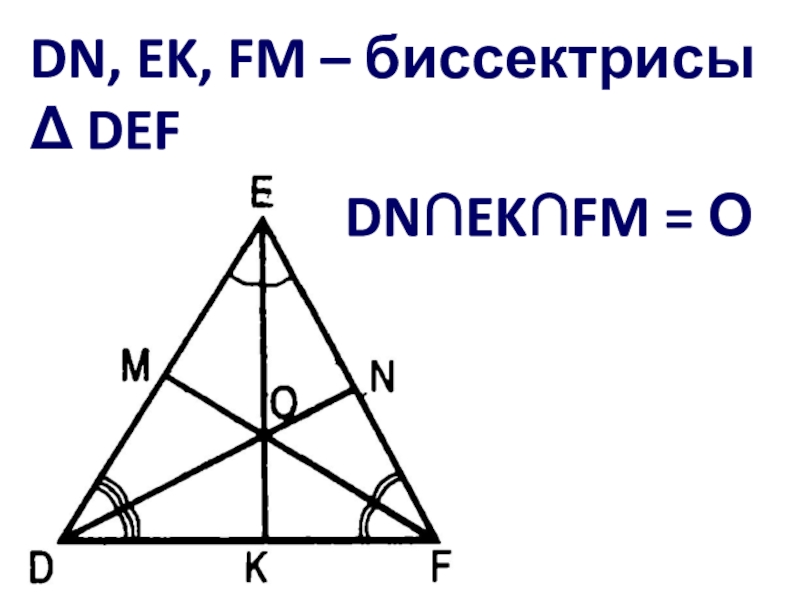
- 22. Начертите DEF и постройте его биссектрисыDN, EK, FM – биссектрисы DEF
- 23. DN, EK, FM – биссектрисы DEF DNEKFM = О
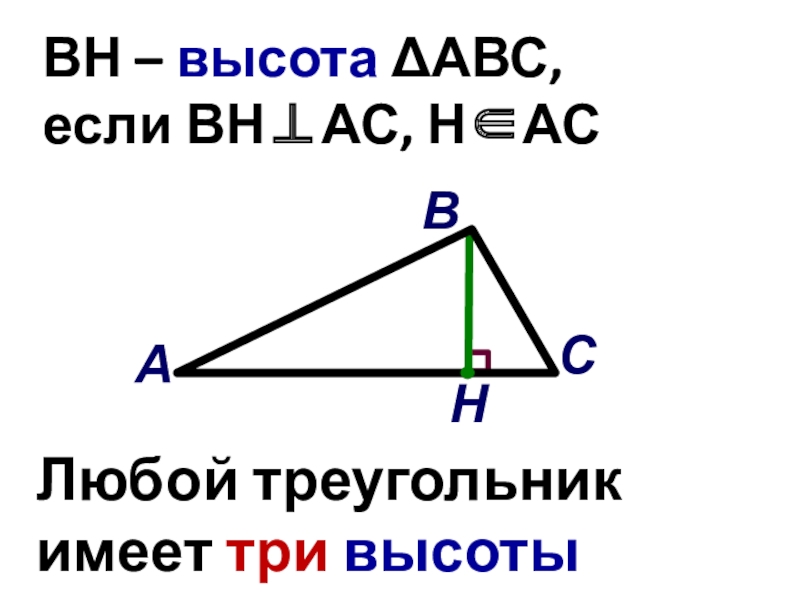
- 24. Перпендикуляр, проведённый из вершины треугольника к прямой, содержащей противоположную сторону, называется высотой треугольника
- 25. СВАВН – высота АВС, если ВНАС, НАСНЛюбой треугольник имеет три высоты
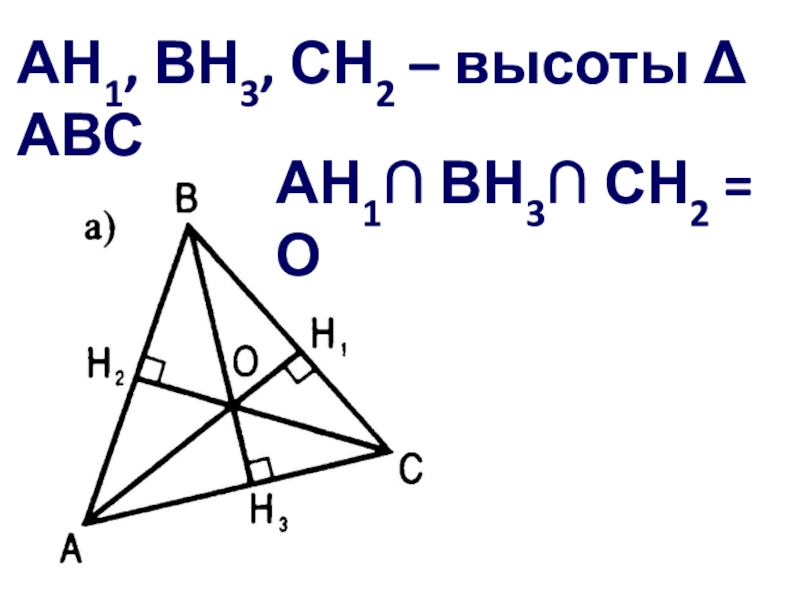
- 26. Начертите остроугольный ABC и постройте его высотыАН1, ВН3, СН2 – высоты АВС
- 27. АН1, ВН3, СН2 – высоты АВС АН1 ВН3 СН2 = О
- 28. Начертите прямоугольный ABC и постройте его высотыАН1, ВН2, СН3 – высоты АВС
- 29. АН1, ВН3, СН2 – высоты АВС АН1 ВН2 СН3 = О
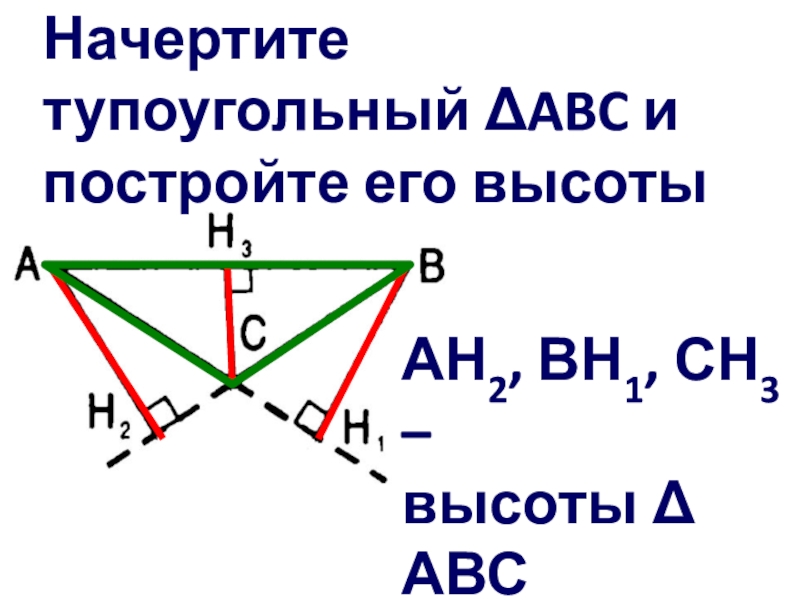
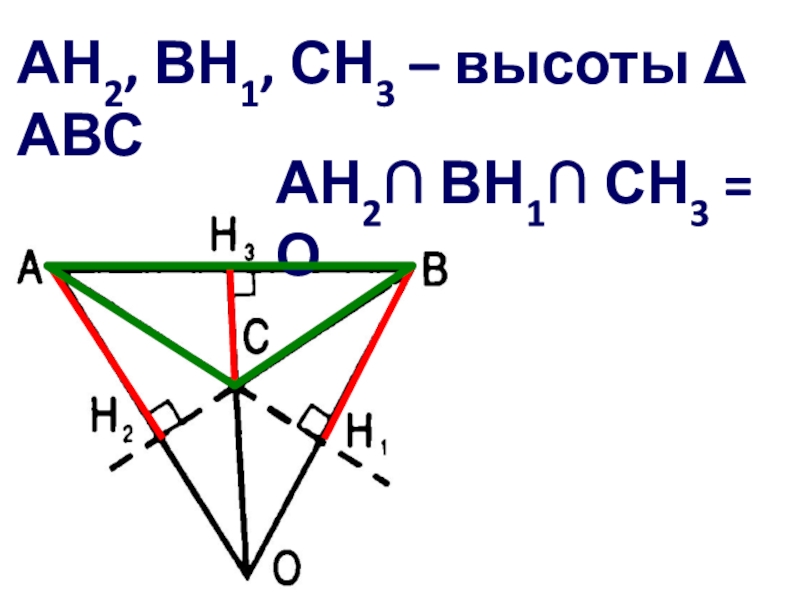
- 30. Начертите тупоугольный ABC и постройте его высотыАН2, ВН1, СН3 – высоты АВС
- 31. АН2, ВН1, СН3 – высоты АВС АН2 ВН1 СН3 = О
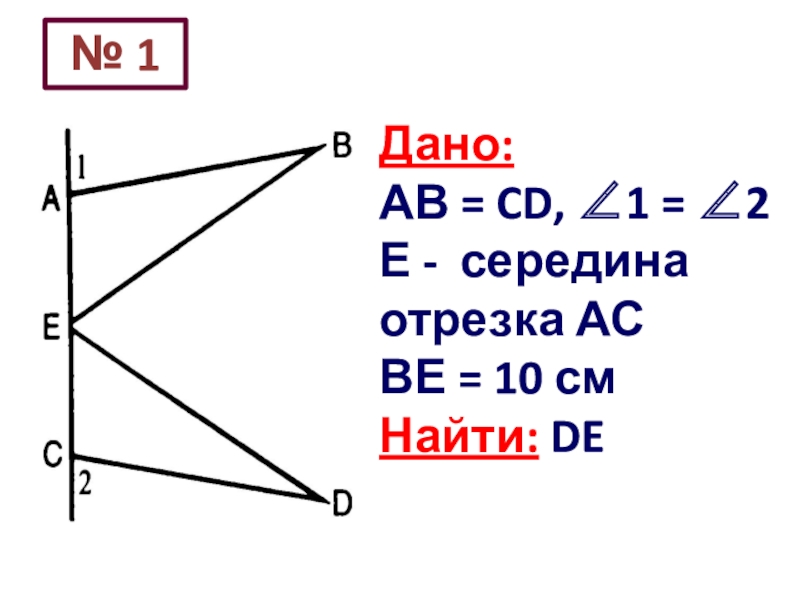
- 32. Дано: АВ = CD, 1 =
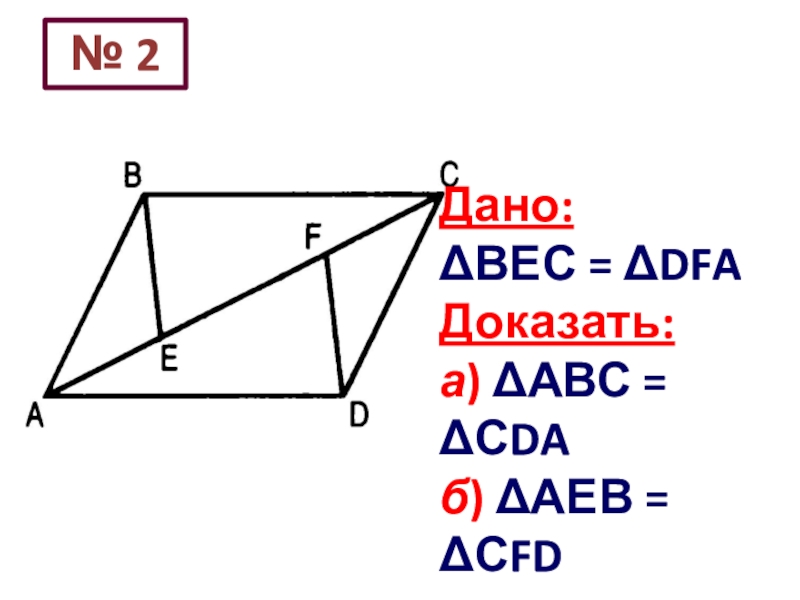
- 33. Дано: ВЕС = DFA Доказать: а) АВС = СDA б) АЕВ = СFD№ 2
- 34. Решение задач№ 105 № 106 (б)
- 35. Домашнее задание № 98№ 99 № 106 (а)№ 100
- 36. Список литературыГеометрия 7-9: учеб. для общеобразоват. Организаций
№ 1Дано: МРС = DAB MP = 12 см, СР = 8 см А = 730812730
Слайд 1Первый признак равенства треугольников.
Медианы, биссектрисы и высоты треугольника.
Кнюк Н.А.,
Учитель математики
МАОУ «Ангарский лицей №1», г. Ангарск
Слайд 12Через точку А проведите прямую, перпендикулярную прямой а. Точку пересечения прямых
обозначьте Н.
а
А
Н
Слайд 15Теорема.
Из точки, не лежащей на прямой, можно провести перпендикуляр к
этой прямой, и притом только один
Слайд 16Отрезок, соединяющий вершину треугольника с серединой противоположной стороны, называется медианой треугольника
Слайд 20Отрезок биссектрисы угла треугольника, соединяющий вершину треугольника с точкой противоположной стороны,
называется биссектрисой треугольника
Слайд 21С
В
А
ВL – биссектриса АВС,
если АBL = CBL, где LАС
L
Любой треугольник
имеет три биссектрисы
Слайд 24Перпендикуляр, проведённый из вершины треугольника к прямой, содержащей противоположную сторону, называется
высотой треугольника
Слайд 36Список литературы
Геометрия 7-9: учеб. для общеобразоват. Организаций с прил. На электрон.
носителе/ [Л.С.Атанасян, В.Ф.Бутузов, С.Б.Кадомцев и д.р.]- М.: Просвещение, 2014
Гаврилова Н.Ф. Универсальные поурочные разработки по геометрии: 7класс.- М.ВАКО, 2010.-(В помощь школьному учителю)
Гаврилова Н.Ф. Универсальные поурочные разработки по геометрии: 7класс.- М.ВАКО, 2010.-(В помощь школьному учителю)
![Список литературыГеометрия 7-9: учеб. для общеобразоват. Организаций с прил. На электрон. носителе/ [Л.С.Атанасян, В.Ф.Бутузов, С.Б.Кадомцев и д.р.]-](/img/thumbs/08cf8a1fc0ec574af1d2a64878618ddc-800x.jpg "Медианы, высоты, биссектрисы. первый признак равенства треугольников Список литературыГеометрия 7-9: учеб. для общеобразоват. Организаций с прил. На электрон.")
