- Главная
- Разное
- Образование
- Спорт
- Естествознание
- Природоведение
- Религиоведение
- Французский язык
- Черчение
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, фоны, картинки для презентаций
- Экология
- Экономика
Презентация, доклад на тему Исследовательская работа по математике Теорема Пифагора
Содержание
- 1. Исследовательская работа по математике Теорема Пифагора
- 2. Цель работызначение теоремы Пифагора в развитии науки
- 3. Биография Пифагора Великий ученый Пифагор
- 4. Биография ПифагораСреди учителей юного Пифагора традиция называет
- 5. Биография ПифагораВ 548 г. до н.э. Пифагор
- 6. Биография ПифагораОднажды к Пифагору приходит Килон, человек
- 7. Формулировки Теоремы Пифагора В
- 8. Формулировки Теоремы ПифагораТо есть, обозначив длину гипотенузы
- 9. Доказательства ТеоремыНа данный момент в научной литературе
- 10. Через подобные треугольники
- 11. 1.Расположим четыре равных
- 12. Доказательства через равносоставленность.
- 13. Обратная теорема Пифагора. Для всякой тройки положительных
Слайд 1Исследовательская работа
Теорема Пифагора
подготовила ученица 8 класса Бабушкина Надежда
Слайд 2Цель работы
значение теоремы Пифагора в развитии науки и практической деятельности человека
Задачи:
1.
2. Ознакомится с различными способами доказательства теоремы Пифагора.
3. Рассмотреть применение теоремы Пифагора при решении задач.
Слайд 3Биография Пифагора
Великий ученый Пифагор родился около 570
Отцом Пифагора был Мнесарх, резчик по драгоценным камням.
Имя же матери Пифагора неизвестно.
По многим античным свидетельствам, родившийся мальчик был сказочно красив, а вскоре проявил и свои незаурядные способности.
Слайд 4Биография Пифагора
Среди учителей юного Пифагора традиция называет имена старца Гермодаманта и
Слайд 5Биография Пифагора
В 548 г. до н.э. Пифагор прибыл в Навкратис -
Слайд 6Биография Пифагора
Однажды к Пифагору приходит Килон, человек богатый, но злой, желая
Слайд 7Формулировки Теоремы Пифагора
В прямоугольном треугольнике площадь квадрата,
Геометрическая формулировка.
Изначально теорема была сформулирована следующим образом:
Слайд 8Формулировки Теоремы Пифагора
То есть, обозначив длину гипотенузы треугольника через c, а
a2 + b2 = c2
Обе формулировки теоремы эквивалентны, но вторая формулировка
более элементарна, она не требует понятия площади.
То есть второе утверждение можно проверить, ничего не зная о
площади и измерив только длины сторон прямоугольного треугольника.
В прямоугольном треугольнике квадрат длины гипотенузы равен сумме квадратов длин катетов.
Алгебраическая формулировка.
Слайд 9Доказательства Теоремы
На данный момент в научной литературе зафиксировано 367 доказательств данной
Разумеется, концептуально все их можно разбить на малое число классов. Самые известные из них: доказательства методом площадей, аксиоматические и экзотические доказательства.
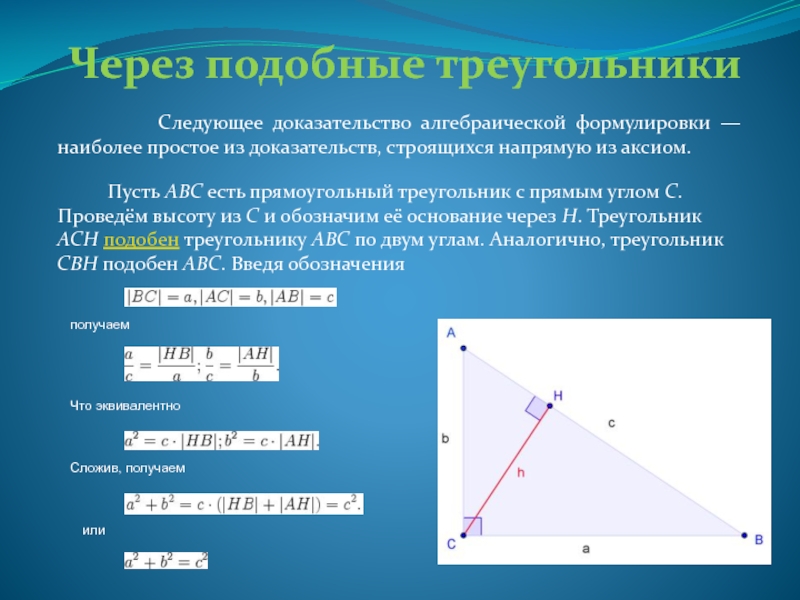
Слайд 10Через подобные треугольники
Следующее доказательство алгебраической формулировки
Пусть ABC есть прямоугольный треугольник с прямым углом C. Проведём высоту из C и обозначим её основание через H. Треугольник ACH подобен треугольнику ABC по двум углам. Аналогично, треугольник CBH подобен ABC. Введя обозначения
получаем
Что эквивалентно
Сложив, получаем
или
Слайд 11 1.Расположим четыре равных прямоугольных треугольника так, как
на рисунке.
2.Четырёхугольник со сторонами c является квадратом, так как сумма двух
острых углов 90°, а развёрнутый угол — 180°.
3.Площадь всей фигуры равна, с одной стороны, площади квадрата со
стороной (a+b), а с другой стороны, сумме площадей четырёх треугольников
и внутреннего квадрата.
Доказательство через равнодополняемость
Что и требовалось доказать.