- Главная
- Разное
- Образование
- Спорт
- Естествознание
- Природоведение
- Религиоведение
- Французский язык
- Черчение
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, фоны, картинки для презентаций
- Экология
- Экономика
Презентация, доклад на тему Исследовательская работа по математике на тему Золотое сечение
Содержание
- 1. Исследовательская работа по математике на тему Золотое сечение
- 2. «Великая книга природы написана математическими символами»
- 3. Введение.Золотое сечение: в математике_______________ в медицине_______________ в растительном миреЗаключение.
- 4. приобрести новые знания по математике в области
- 5. 1. Познакомиться с понятием золотого сечения. 2.
- 6. Слайд 6
- 7. Целое всегда состоит из частей, части разной
- 8. «Золотое сечение» в математике.Иоганн Кеплер говорил, что
- 9. Что такое «золотое сечение»? Говорят, что точка
- 10. Геометрически «золотое сечение» отрезка АВ можно построить
- 11. Золотой треугольник.Золотым называется такой равнобедренный треугольник ,
- 12. Золотой прямоугольникПрямоугольник стороны которого находятся в золотом
- 13. Замечательный пример «золотого сечения» представляет собой правильный
- 14. Некто поместил пару кроликов в некоем месте,
- 15. Ясно, что если считать первую пару кроликов
- 16. Из этой задачи последовало открытие некого ряда
- 17. «Золотое сечение» в работах Леонардо да Винчи
- 18. Витрувианский человек.В сопроводительных записях Леонардо да Винчи
- 19. Портрет Монны Лизы (Джоконды), написанный Леонардо да
- 20. «Золотое сечение» в медицине.Внимание, которого удостоилось золотое
- 21. Пусть рост человека измерен и соответствует длине
- 22. Каждая отдельная часть тела - голова, рука,
- 23. Схема принципа расчета золотой меры на теле
- 24. Рука человекаСумма двух первых фаланг пальца в
- 25. Золотое сечение в чертах лица человека как
- 26. «Идеальная улыбка»если мы суммируем ширину двух передних
- 27. Рис.8Недавно наш современник, американский хирург Стивен Маркварт
- 28. Человек, как и другие творения природы, подчиняется
- 29. Золотая пропорция в строении легких человека.Американский физик
- 30. Ритмы сердца.В артериях во время систолы желудочков
- 31. Золотые пропорции в строении молекулы ДНК.Все сведения
- 32. «Золотое сечение» в растительном мире.«Золотое сечение» встречается
- 33. Среди придорожных трав растет ничем не примечательное
- 34. В ящерице с первого взгляда улавливаются приятные
- 35. Спираль Архимеда
- 36. Слайд 36
- 37. Слайд 37
- 38. Слайд 38
- 39. Слайд 39
- 40. Заключение. Изучив более подробно «золотое сечение» и
- 41. Литература1.Энциклопедичкский словарь юного математика- М.: Педагогика,1989 г.2.
- 42. Спасибо за внимание !
Слайд 1МОУ гимназия №11
Проект на тему:
«Золотое сечение»
Руководитель Малечкина Т.К. учитель математики
I квалификационной категории
Слайд 2«Великая книга природы написана математическими символами»
«Никакое человеческое исследование не может быть названо истиной, если оно не проходит через математическое доказательство»
Леонардо да Винчи
«Числа не управляют миром, но они показывают, как управлять миром».
И. Гете
Слайд 3
Введение.
Золотое сечение: в математике
_______________ в медицине
_______________ в растительном мире
Заключение.
Слайд 4приобрести новые знания по математике в области «Золотого сечения» и их
Цель исследования:
Слайд 51. Познакомиться с понятием золотого сечения.
2. Рассмотреть присутствие «золотых» пропорций
3. Выяснить, как используется золотое сечение человеком в медицине.
4. Определить, как мне эти знания могут пригодиться в выборе моей будущей профессии.
Задачи
Слайд 6 Гипотеза
Изучив золотое сечение как
Слайд 7
Целое всегда состоит из частей, части разной величины находятся в определенном
Феномен золотого сечения известен человечеству очень давно. Его тайну пытались осмыслить Платон, Евклид, Пифагор, Леонардо да Винчи, Кеплер и многие другие крупнейшие мыслители человечества. Они неразрывно связывали золотое сечение с понятием всеобщей гармонии, пронизывающей вселенную от микромира до макрокосмоса.
Принято считать, что понятие о золотом делении ввел в научный обиход Пифагор, древнегреческий философ и математик (VI в. до н.э.).
Слайд 8«Золотое сечение» в математике.
Иоганн Кеплер говорил, что геометрия владеет двумя сокровищами
Теорему Пифагора знает каждый, а вот что такое «золотое сечение» — далеко не все. Расскажем вам об этом «драгоценном камне».
Слайд 9Что такое «золотое сечение»? Говорят, что точка C производит «золотое сечение»
Итак, «золотое сечение» - это такое деление целого на две неравные части, при котором бόльшая часть так относится к целому, как меньшая к бόльшей.
Если принять длину отрезка АВ за 100 единиц измерения, то длина отрезка АС будет равна примерно 62, а длина отрезка СВ - 38 единицам измерения.
Слайд 10
Геометрически «золотое сечение» отрезка АВ можно построить следующим образом: восстановить в
Рис.2
Слайд 11Золотой треугольник.
Золотым называется такой равнобедренный треугольник , основание и боковая сторона
B
A
C
Слайд 12Золотой прямоугольник
Прямоугольник стороны которого находятся в золотом отношении т.е. отношение длины
L
M
K
N
Слайд 13Замечательный пример «золотого сечения» представляет собой правильный звездчатый пятиугольник. (рис. 4).
Можно
АС : АВ = СВ : АС≈1:1,618≈0,62.
Таким образом, звездчатый пятиугольник также обладает «золотым сечением». Интересно, что внутри пятиугольника можно продолжить строить пятиугольники, и это отношение будет сохраняться.
Замечательный пример «золотого сечения» представляет собой правильный звездчатый пятиугольник. (рис. 4).
Можно вывести уже известную пропорцию:
АС : АВ = СВ : АС≈1:1,618≈0,62.
Таким образом, звездчатый пятиугольник также обладает «золотым сечением». Интересно, что внутри пятиугольника можно продолжить строить пятиугольники, и это отношение будет сохраняться.
Рис4
Слайд 14
Некто поместил пару кроликов в некоем месте, огороженном со всех сторон
Задача о кроликах
Слайд 15
Ясно, что если считать первую пару кроликов новорожденными, то на второй
на 3-й месяц - 1+1=2;
на 4-й месяц - 2+1=3 пары (ибо из двух имеющихся пар потомство дает лишь одна пара);
на 5-й месяц - 3+2=5 пар (лишь 2 родившиеся на 3-й месяц пары дадут потомство на 5-й месяц);
на 6-й месяц - 5+3=8 пар (ибо потомство дадут только те пары, которые родились на 4-м месяце) и т. д.
Слайд 16Из этой задачи последовало открытие некого ряда последовательности натуральных чисел каждый
Uk=1,1,2,3,5,8,13,21,34,55,89,144,233,377,...,
Такая последовательность получила название Последовательность Фибоначчи, а её члены числами Фибоначчи. Отношение последующего члена ряда к предыдущему стремится к коэффициенту золотого сечения
В алгебре общепринято его обозначение греческой буквой фи
Ф≈1.618
Слайд 17«Золотое сечение» в работах Леонардо да Винчи
Переходя к примерам «золотого
Многие теоретики считают, что термин «золотое сечение» ввёл Леонардо да Винчи ( конец 15 начало 16 вв.).
Леонардо да Винчи
Слайд 18Витрувианский человек.
В сопроводительных записях Леонардо да Винчи указал, что рисунок был
Слайд 19Портрет Монны Лизы (Джоконды), написанный Леонардо да Винчи, долгие годы привлекает
Джоконда
Слайд 20«Золотое сечение» в медицине.
Внимание, которого удостоилось золотое сечение, связано с тем,
Деление тела точкой пупа — важнейший показатель золотого сечения. Пропорции мужского тела колеблются в пределах среднего отношения 13:8=1,625 и несколько ближе подходят к золотому сечению, чем пропорции женского тела, в отношении которого среднее значение пропорции выражается в соотношении 8:5=1,6. У новорожденного пропорция составляет отношение 1:1, к 13 годам она равна 1,6, а к 21 году равняется мужской. Пропорции золотого сечения проявляются в отношении разных частей тела — роста, длины плеча, предплечья и кисти, кисти и пальцев, ширины плеч. Все отрезки для измерений тела образуют между собой соотношения золотого сечения.
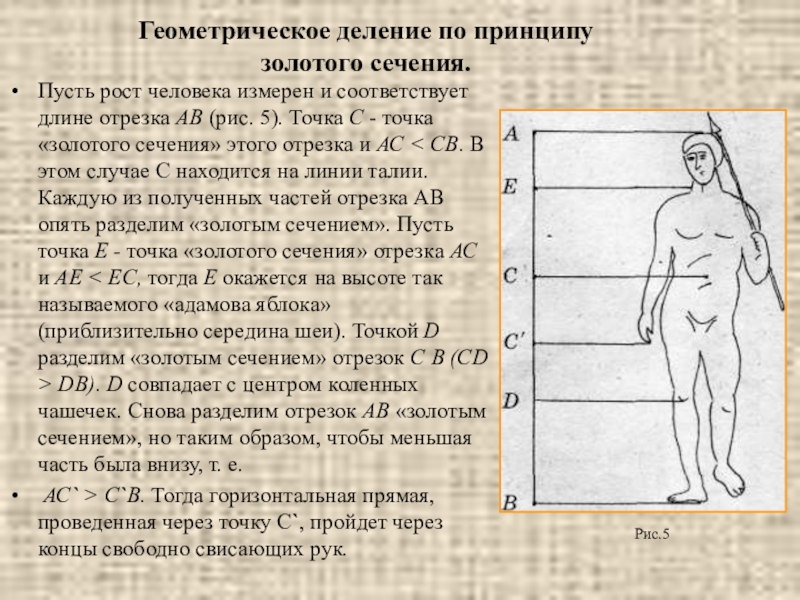
Слайд 21Пусть рост человека измерен и соответствует длине отрезка АВ (рис. 5).
АС` > С`В. Тогда горизонтальная прямая, проведенная через точку С`, пройдет через концы свободно свисающих рук.
Рис.5
Геометрическое деление по принципу золотого сечения.
Слайд 22Каждая отдельная часть тела - голова, рука, кисть и т. д.
Рис.5
Рис.6 Рис.7
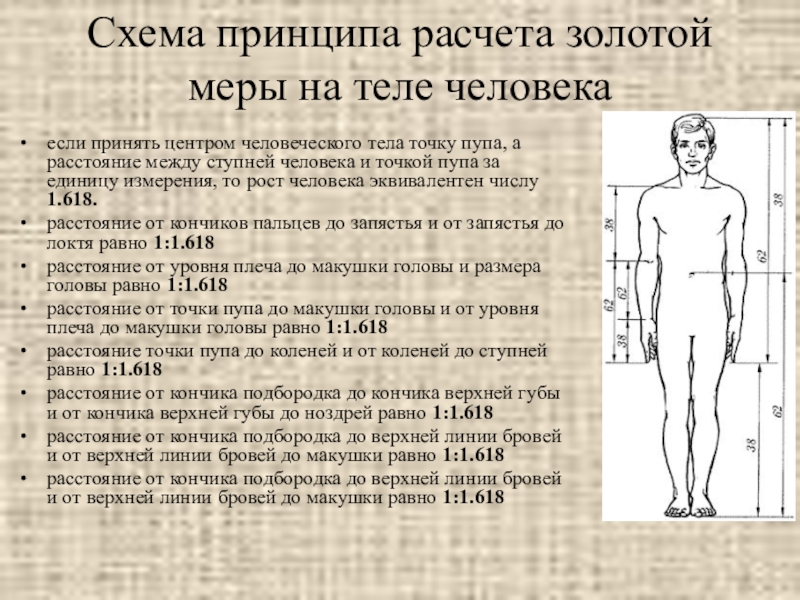
Слайд 23Схема принципа расчета золотой меры на теле человека
если принять центром человеческого
расстояние от кончиков пальцев до запястья и от запястья до локтя равно 1:1.618
расстояние от уровня плеча до макушки головы и размера головы равно 1:1.618
расстояние от точки пупа до макушки головы и от уровня плеча до макушки головы равно 1:1.618
расстояние точки пупа до коленей и от коленей до ступней равно 1:1.618
расстояние от кончика подбородка до кончика верхней губы и от кончика верхней губы до ноздрей равно 1:1.618
расстояние от кончика подбородка до верхней линии бровей и от верхней линии бровей до макушки равно 1:1.618
расстояние от кончика подбородка до верхней линии бровей и от верхней линии бровей до макушки равно 1:1.618
Слайд 24Рука человека
Сумма двух первых фаланг пальца в соотношении со всей длиной
Кроме того, соотношение между средним пальцем и мизинцем также равно числу золотого сечения.
У человека 2 руки, пальцы на каждой руке состоят из 3 фаланг (за исключением большого пальца). На каждой руке имеется по 5 пальцев, то есть всего 10, но за исключением двух двухфаланговых больших пальцев только 8 пальцев создано по принципу золотого сечения. Тогда как все эти цифры 2, 3, 5 и 8 есть числа последовательности Фибоначчи.
Слайд 25Золотое сечение в чертах лица человека как критерий совершенной красоты.
Высота лица
Центральная точка соединения губ до основания носа / длина носа.
Высота лица / расстояние от кончика подбородка до центральной точки соединения губ
Ширина рта / ширина носа,
Ширина носа / расстояние между ноздрями,
Расстояние между зрачками / расстояние между бровями.
Все эти отношения равны числу Ф≈1.618
Слайд 26«Идеальная улыбка»
если мы суммируем ширину двух передних верхних зубов и разделим
Слайд 27
Рис.8
Недавно наш современник, американский хирург Стивен Маркварт создал, используя принцип «золотого
Слайд 28Человек, как и другие творения природы, подчиняется всеобщим законам развития. Корни
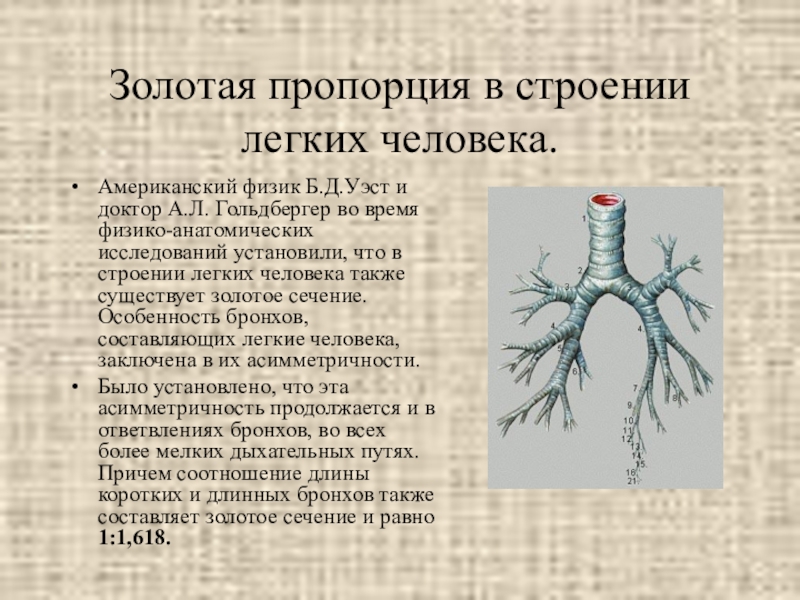
Слайд 29Золотая пропорция в строении легких человека.
Американский физик Б.Д.Уэст и доктор А.Л.
Было установлено, что эта асимметричность продолжается и в ответвлениях бронхов, во всех более мелких дыхательных путях. Причем соотношение длины коротких и длинных бронхов также составляет золотое сечение и равно 1:1,618.
Слайд 30Ритмы сердца.
В артериях во время систолы желудочков сердца кровяное давление достигает
На кардиограмме сердца выделяется два участка различной длительности, соответствующие систолической (t1) и диастолической (t2) деятельности сердца. В.Д. Цветков установил, что у человека и у других млекопитающих имеется оптимальная ("золотая") частота сердцебиения, при которой длительности систолы, диастолы и полного сердечного цикла (T) соотносятся в пропорции золотого сечения, то есть
T : t2 = t2 : t1≈1,618.
Так например, для человека эта "золотая" частота равна 63 ударам сердца в минуту, для собак - 94, что отвечает реальной частоте сердцебиения в состоянии покоя.
интервал RR – полный сердечный цикл (Т)
интервал QT – систола сердца (t1)
сегмент ТР - диастола (t2)
T=3,9 t1=1,5 t2=2,4
3,9:2,4≈1,625 2,4:1,5≈1,6
Слайд 31Золотые пропорции в строении молекулы ДНК.
Все сведения о физиологических особенностях живых
Слайд 32«Золотое сечение» в растительном мире.
«Золотое сечение» встречается в растительном мире. Рассматривая
Рис.4
Слайд 33Среди придорожных трав растет ничем не примечательное растение – цикорий. Приглядимся
Рис. 1. Цикорий
Отросток делает сильный выброс в пространство, останавливается, выпускает листок, но уже короче первого, снова делает выброс в пространство, но уже меньшей силы, выпускает листок еще меньшего размера и снова выброс. Если первый выброс принять за 100 единиц, то второй равен 62 единицам, третий – 38, четвертый – 24 и т.д. Длина лепестков тоже подчинена золотой пропорции. В росте, завоевании пространства растение сохраняло определенные пропорции. Импульсы его роста постепенно уменьшались в пропорции золотого сечения.
Слайд 34В ящерице с первого взгляда улавливаются приятные для нашего глаза пропорции
Рис. 1. Ящерица живородящая
И в растительном, и в животном мире настойчиво пробивается формообразующая тенденция природы – симметрия относительно направления роста и движения. Здесь золотое сечение проявляется в пропорциях частей перпендикулярно к направлению роста.
Рис.2. Яйцо птицы
Слайд 40Заключение.
Изучив более подробно «золотое сечение» и его проявления в живой
Кроме того, эти вопросы выходят за рамки школьного курса, они способствуют совершенствованию и развитию важнейших математических умений.
Таким образом, приобретенные знания о золотой пропорции, еще больше убедили нас в необходимости изучения математики как неотъемлемой части нашей будущей профессии.
Слайд 41Литература
1.Энциклопедичкский словарь юного математика- М.: Педагогика,1989 г.
2. Я познаю мир: Детская
3. Депман, И.Я.Виленкин, За страницами учебника математики- М.: Просвещение,1989 г.
4. Васютинский,Н.Н. Золотая пропорция.- М.: Молода гвардия, 1990 г.
5. Газета «Математика», приложение к учебно-методическому пособию «Первое сентября».-М.: издательский дом «Первое сентября», 2007.
6. Квант: научно-популярная физико-математическая энциклопедия. - М.: Бюро «Квантум».
7. Информация из интернета.