студент 2 курса группы МК-24
Аксуского колледж черной
металлургии»: Куандыков Жанибек
- Главная
- Разное
- Образование
- Спорт
- Естествознание
- Природоведение
- Религиоведение
- Французский язык
- Черчение
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, фоны, картинки для презентаций
- Экология
- Экономика
Презентация, доклад на тему Электронное учебное пособие по геметрии Взаимное расположение прямых и плоскостей в пространстве
Содержание
- 1. Электронное учебное пособие по геметрии Взаимное расположение прямых и плоскостей в пространстве
- 2. В электронном учебном пособии «Взаимное расположение прямых
- 3. Цель:Активизация познавательной деятельности обучающихся
- 4. Взаимное расположение прямых и плоскостей в пространствеВзаимное
- 5. Взаимное расположение прямых в пространствеНАЗАДПараллельные прямыеПересекающиеся прямыеПерпендикулярные прямыеСкрещивающиеся прямыеЗаданияДиктант
- 6. Параллельные прямые
- 7. Параллельные прямые Параллельными прямыми называются прямые, которые лежат в одной плоскости и не пересекаются.
- 8. Аксиома: Через любую точку пространства, не лежащую
- 9. Признаки параллельности прямых: Две прямые, параллельные
- 10. Пересекающиеся прямые
- 11. Пересекающиеся прямыеДве прямые называются пересекающимися если лежат в одной плоскости и имеют общую точку.НАЗАД
- 12. Перпендикулярные прямые
- 13. Перпендикулярные прямыеДве прямые, которые лежат в одной
- 14. Теорема: если две пересекающиеся прямые одной плоскости
- 15. Скрещивающиеся прямые Две прямые называются скрещивающимися, если они лежат в разных плоскостях.Видео «Скрещивающиеся прямые»НАЗАД
- 16. Признак скрещивающихся прямыхЕсли одна прямая лежит в
- 17. Взаимное расположение плоскостей в пространстве Параллельные плоскостиПересекающиеся плоскостиПерпендикулярные плоскостиСовпадающие плоскостиЗаданияНАЗАД
- 18. Плоскости, не пересекающиеся и не имеющие общих точек, называются параллельными1. Параллельные плоскостиВидео «Параллельность плоскостей»НАЗАД
- 19. Признак: Если две пересекающиеся прямые одной плоскости
- 20. Свойства параллельности плоскостей1. Если две параллельные плоскости
- 21. 2. Пересекающиеся плоскости Плоскости называются
- 22. 2. Перпендикулярные плоскостиПлоскости, которые пересекаются под прямым
- 23. Признак перпендикулярности двух плоскостей: Если одна
- 24. Плоскости совпадаютПлоскости, которые имеют множество общих точек , называются совпадающими.НАЗАД
- 25. Взаимное расположение прямых и плоскостей в пространствеПараллельность
- 26. Параллельность плоскости и прямой Прямая и
- 27. Признак параллельности прямой и плоскостиЕсли прямая, не
- 28. Пересечение плоскости и прямой Плоскость и
- 29. Перпендикулярность плоскости и прямой
- 30. Признак перпендикулярности прямой и плоскостиЕсли прямая, пересекающая
- 31. Свойства перпендикулярности прямой и плоскости1. Если плоскость,
- 32. Прямая лежит в плоскости
- 33. Закончите предложения:1. Две прямые называются перпендикулярными, если…2.
- 34. Задание 1.Каково может быть взаимное расположение прямых
- 35. Каково может быть взаимное расположение плоскостей в пространстве?АBCDА1B1C1D1????Задание 2.IIII∩∩НАЗАД
- 36. АBCDА1B1C1D1Каково может быть взаимное расположение прямых и плоскостей в пространстве????Задание 1.???НАЗАД
- 37. 1. Дан прямоугольный параллелепипед ABCDA1B1C1D1. Выберите правильное утверждение.А. Прямая
- 38. НАЗАД
- 39. 1) Прямую, перпендикулярную любой прямой в плоскости, называют...а) наклонной к плоскости; б) перпендикуляром к плоскости; в) секущей; г) лучом.2) Параллельными называют плоскости,...а) не имеющие общих прямых; б) у которых одна общая точка;в) у которых две общих точки; г) не имеющие ни одной общей точки.3) Прямая параллельна плоскости, если они...а) пересекают прямую в одной и той же точке;б) перпендикулярны одной и той же прямой;в) удалены от данной точки на равные расстояния;г)
- 40. 7) Если две параллельные плоскости пересечь третьей, то . . .а) линии пересечения равны;б) линии пересечения параллельны;в) линии пересечения перпендикулярны;г)
- 41. 12) Прямые, имеющие одну общую точку называют . . .а) скрещивающимися; б) пересекающимися; в) параллельными; г) совпадающими.13) Две плоскости параллельны, если они . . .а) перпендикулярны одной и той же прямой;б) параллельны одной и той же прямой;в) пересекаются в одной точке;г) пересекают одну и ту же прямую,14) Если две прямые параллельны третьей, то они . . .а) перпендикулярны друг другу; б) параллельны между собой;
- 42. параллельныепересекающиесяперпендикулярныележитИмеют множество общих точекИмеют одну общую точкуНе
- 43. ЛитератураГусев В. , Кайдасов Ж., Кагабаева А.
В электронном учебном пособии «Взаимное расположение прямых и плоскостей в пространстве» разработан необходимый материал по формированию основных знаний, умений и навыков студентов по разделу геометрии общеобразовательных дисциплин. В электронное пособие вошел
Слайд 1Взаимное расположение прямых и плоскостей в пространстве
Электронное учебное
пособие по геометрии
Автор:
Слайд 2В электронном учебном пособии «Взаимное расположение прямых и плоскостей в пространстве»
разработан необходимый материал по формированию основных знаний, умений и навыков студентов по разделу геометрии общеобразовательных дисциплин.
В электронное пособие вошел материал по стереометрии, изучающий взаимное расположение прямых и плоскостей в пространстве. Каждый раздел пособия содержит краткий обзор теоретического материала, также имеются задания на знания характеристик расположения прямых и плоскостей в пространстве, тестовый контроль знаний, видеоматериал по теме «Взаимное расположение прямых и плоскостей в пространстве».
Электронное учебное пособие может использоваться, как при теоретическом и практическом обучении студентов учебных заведений, так и при самостоятельном повышении качества знаний по геометрии по темам стереометрии.
В электронное пособие вошел материал по стереометрии, изучающий взаимное расположение прямых и плоскостей в пространстве. Каждый раздел пособия содержит краткий обзор теоретического материала, также имеются задания на знания характеристик расположения прямых и плоскостей в пространстве, тестовый контроль знаний, видеоматериал по теме «Взаимное расположение прямых и плоскостей в пространстве».
Электронное учебное пособие может использоваться, как при теоретическом и практическом обучении студентов учебных заведений, так и при самостоятельном повышении качества знаний по геометрии по темам стереометрии.
Слайд 3Цель:
Активизация познавательной деятельности обучающихся на уроках геометрии в
процессе применения электронного учебного пособия.
Обучение пониманию изучаемого материала за счет информационно - коммуникационных технологий.
Формирование устойчивого интереса к учебе, к знаниям и потребности в их самостоятельном поиске.
Обучение пониманию изучаемого материала за счет информационно - коммуникационных технологий.
Формирование устойчивого интереса к учебе, к знаниям и потребности в их самостоятельном поиске.
Слайд 4Взаимное расположение прямых и плоскостей в пространстве
Взаимное расположение прямых в пространстве
Взаимное
расположение плоскостей в пространстве
Взаимное расположение прямых и плоскостей в пространстве
Взаимное расположение прямых и плоскостей в пространстве
Видео
«Прямые и плоскости в пространстве
Тесты
Тестовые задания
Слайд 5Взаимное расположение
прямых в пространстве
НАЗАД
Параллельные прямые
Пересекающиеся прямые
Перпендикулярные прямые
Скрещивающиеся прямые
Задания
Диктант
Слайд 7 Параллельные прямые
Параллельными прямыми
называются
прямые, которые
лежат в
одной плоскости и
не пересекаются.
не пересекаются.
Слайд 8Аксиома: Через любую точку пространства, не лежащую на данной прямой, проходит
прямая, параллельная данной, и притом только одна
a
М
b
M ∉ a
α
a, M ∈ α
a, b ∈ α
M ∈ b, b ∥ a ⇒
⇒ b ∈ α ⇒
⇒ b — единственная
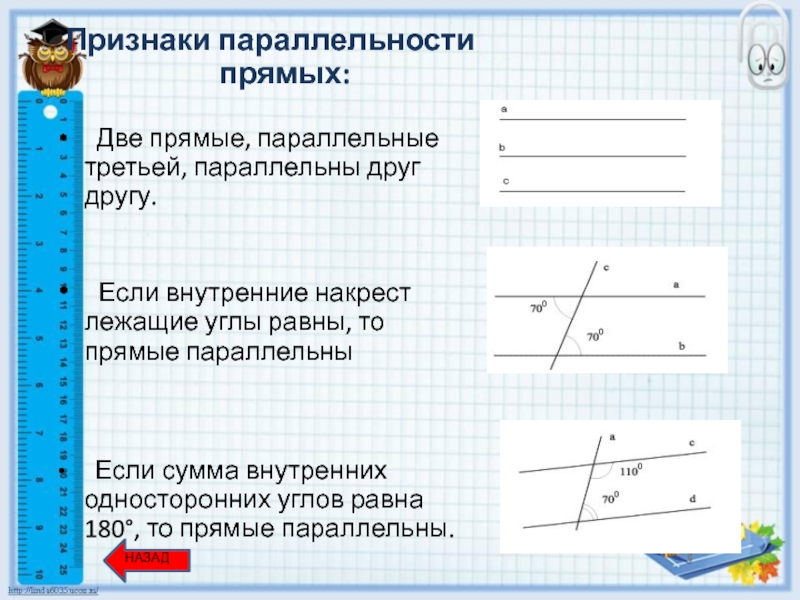
Слайд 9Признаки параллельности прямых:
Две прямые, параллельные третьей, параллельны друг
другу.
Если внутренние накрест лежащие углы равны, то прямые параллельны
Если сумма внутренних односторонних углов равна 180°, то прямые параллельны.
Если внутренние накрест лежащие углы равны, то прямые параллельны
Если сумма внутренних односторонних углов равна 180°, то прямые параллельны.
НАЗАД
Слайд 11Пересекающиеся прямые
Две прямые называются
пересекающимися
если лежат в одной плоскости
и
имеют общую точку.
НАЗАД
Слайд 13Перпендикулярные прямые
Две прямые, которые
лежат в одной
плоскости пересекаются
под прямым
углом
называются
перпендикулярными.
называются
перпендикулярными.
Видео «Перпендикулярные прямые»
НАЗАД
Слайд 14Теорема: если две пересекающиеся прямые одной плоскости параллельны соответственно двум пересекающимся
прямым другой плоскости, то они перпендикулярны.
a
b
c
d
НАЗАД
Слайд 15Скрещивающиеся прямые
Две прямые называются скрещивающимися, если они лежат в
разных плоскостях.
Видео «Скрещивающиеся прямые»
НАЗАД
Слайд 16Признак скрещивающихся прямых
Если одна прямая лежит в данной плоскости, а другая
прямая пересекает эту плоскость в точке
не принадлежащей первой прямой, то эти две прямые скрещивающиеся.
не принадлежащей первой прямой, то эти две прямые скрещивающиеся.
а
b
Слайд 17Взаимное расположение
плоскостей в пространстве
Параллельные плоскости
Пересекающиеся плоскости
Перпендикулярные плоскости
Совпадающие плоскости
Задания
НАЗАД
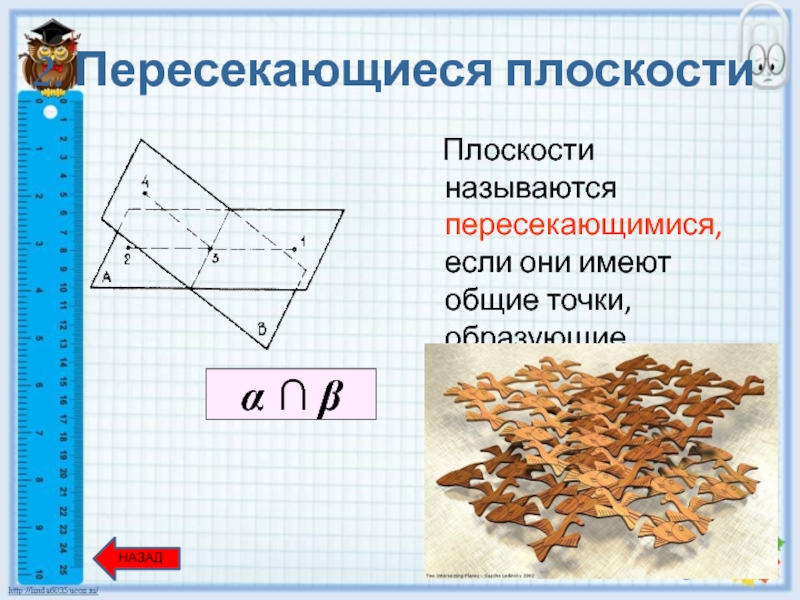
Слайд 18
Плоскости, не пересекающиеся и не имеющие общих точек, называются
параллельными
1. Параллельные плоскости
Видео «Параллельность
плоскостей»
НАЗАД
Слайд 19Признак: Если две пересекающиеся прямые одной плоскости соответственно параллельны двум прямым
другой плоскости, то эти плоскости параллельны.
α
β
а
b
М
b1
а1
М1
а ∩ b = М; а Є α; b Є α
а1∩ b1 = М1; а1Є β; b1Є β
a || a1; b || b1
α || β
Слайд 20Свойства параллельности плоскостей
1. Если две параллельные плоскости пересечены третьей, то линии
их пересечения параллельны
γ
α
β
a
b
γ ∩ α = a
γ ∩ β = b
a ‖ b
α
‖
β
2. Отрезки параллельных прямых, заключенные между параллельными плоскостями, равны.
α
β
γ
A
B
C
D
⇒ AB = CD
⇒ АС ∥ BD
α ∥ β
AB ∥ CD
γ ∩ α = АC
γ ∩ β = BD
α
‖
β
⇒
ABCD –
параллелограмм
Слайд 21 2. Пересекающиеся плоскости
Плоскости называются пересекающимися, если они имеют
общие точки, образующие прямую.
α ∩ β
НАЗАД
Слайд 222. Перпендикулярные плоскости
Плоскости, которые пересекаются под прямым углом , называются перпендикулярными
b
а
Слайд 23Признак перпендикулярности двух плоскостей: Если одна из плоскостей проходит через прямую,
перпендикулярную другой плоскости, то эти плоскости перпендикулярны.
НАЗАД
Слайд 24Плоскости совпадают
Плоскости, которые имеют множество общих точек , называются совпадающими.
НАЗАД
Слайд 25Взаимное расположение прямых и плоскостей в пространстве
Параллельность плоскости и прямой
Прямая лежит
в плоскости
Пересечение плоскости и прямой
Перпендикулярность плоскости и прямой
Задания 1 2
НАЗАД
Слайд 26Параллельность
плоскости и прямой
Прямая и плоскость называются параллельными, если
они не пересекаются и не имеют общих точек
НАЗАД
Слайд 27Признак параллельности
прямой и плоскости
Если прямая, не лежащая в данной плоскости,
параллельна какой-нибудь прямой в этой плоскости, то она параллельна и самой плоскости.
а1
а
α
а || а1
а || α
Слайд 28Пересечение плоскости и прямой
Плоскость и прямая называются пересекающимися, если
они имеют одну общую точку пересечения.
B
НАЗАД
Слайд 29 Перпендикулярность
плоскости и прямой
Прямая, называется перпендикулярной к
плоскости, если она перпендикулярна к любой прямой, которая лежит в данной плоскости.
Видео «Перпендикулярность прямой и
плоскостей»
НАЗАД
Слайд 30Признак перпендикулярности прямой и плоскости
Если прямая, пересекающая плоскость,
перпендикулярна к двум
прямым этой
плоскости, проходящим через точку
пересечения, то она перпендикулярна
к плоскости.
плоскости, проходящим через точку
пересечения, то она перпендикулярна
к плоскости.
a
bв
c
b
с
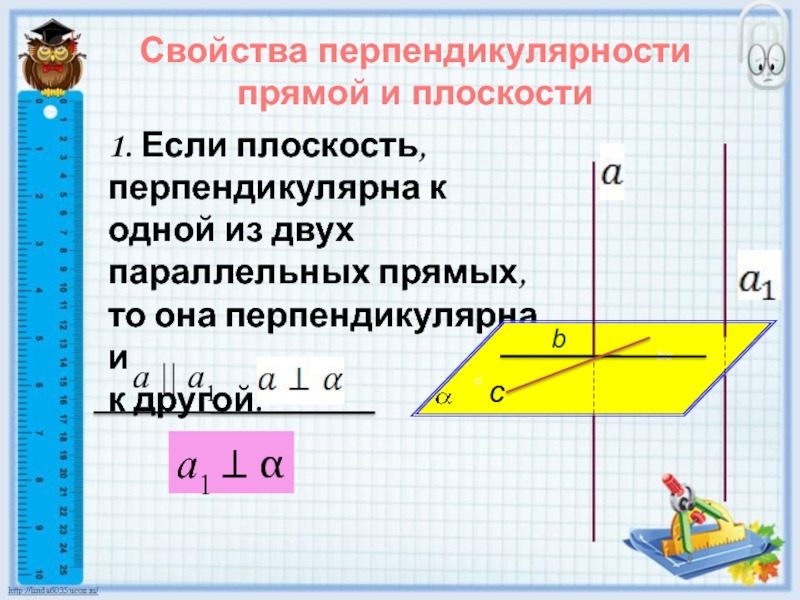
Слайд 31Свойства перпендикулярности прямой и плоскости
1. Если плоскость,
перпендикулярна к одной из
двух параллельных прямых, то она перпендикулярна и
к другой.
к другой.
bв
c
b
с
а || а1
а1
⊥ α
Слайд 32 Прямая лежит в плоскости
Если прямая и плоскость
имеют множество общих точек , то прямая лежит в плоскости.
НАЗАД
Слайд 33Закончите предложения:
1. Две прямые называются перпендикулярными, если…
2. Прямая называется перпендикулярной к
плоскости, если…
3.Прямая перпендикулярна плоскости, если она…
4.Если одна из двух параллельных прямых перпендикулярна к третьей прямой, то…
5.Через данную точку пространства можно провести прямую, перпендикулярную данной плоскости, и притом …
6. Все прямые, проходящие через данную точку прямой и перпендикулярные к этой прямой, лежат в …
7. Если одна из двух параллельных прямых перпендикулярна плоскости, то…
8. Две прямые, перпендикулярные одной и той же плоскости,…
9. Если плоскость перпендикулярна одной из двух параллельных прямых, то …
10. Если две плоскости перпендикулярны прямой, то они …
3.Прямая перпендикулярна плоскости, если она…
4.Если одна из двух параллельных прямых перпендикулярна к третьей прямой, то…
5.Через данную точку пространства можно провести прямую, перпендикулярную данной плоскости, и притом …
6. Все прямые, проходящие через данную точку прямой и перпендикулярные к этой прямой, лежат в …
7. Если одна из двух параллельных прямых перпендикулярна плоскости, то…
8. Две прямые, перпендикулярные одной и той же плоскости,…
9. Если плоскость перпендикулярна одной из двух параллельных прямых, то …
10. Если две плоскости перпендикулярны прямой, то они …
Диктант.
НАЗАД
Слайд 34Задание 1.
Каково может быть взаимное расположение прямых в пространстве?
А
B
C
D
А1
B1
C1
D1
AB и CD
B1C
и C1C
AD1 и A1D
BC и AA1
B1C и A1D
AD1 и A1D
BC и AA1
B1C и A1D
II
?
∩
?
∩
?
?
?
НАЗАД
Слайд 35Каково может быть взаимное расположение плоскостей в пространстве?
А
B
C
D
А1
B1
C1
D1
?
?
?
?
Задание 2.
II
II
∩
∩
НАЗАД
Слайд 36А
B
C
D
А1
B1
C1
D1
Каково может быть взаимное расположение прямых и плоскостей в пространстве?
?
?
?
Задание 1.
?
?
?
НАЗАД
Слайд 371. Дан прямоугольный параллелепипед ABCDA1B1C1D1.
Выберите правильное утверждение.
А. Прямая DC параллельна плоскости ABC.
Б. Прямая
DC пересекает плоскость ABB1.
В. Прямая DC параллельна плоскости, которая проходит через прямые AA1 и CC1.
Г. Прямая DC имеет общие точки с плоскостью BB1C1.
В. Прямая DC параллельна плоскости, которая проходит через прямые AA1 и CC1.
Г. Прямая DC имеет общие точки с плоскостью BB1C1.
Тестовые задания
Слайд 391) Прямую, перпендикулярную любой прямой в плоскости, называют...
а) наклонной к плоскости; б) перпендикуляром к плоскости; в) секущей; г) лучом.
2) Параллельными называют плоскости,...
а) не имеющие общих прямых; б) у которых одна общая точка;
в) у которых две общих точки; г) не имеющие ни одной общей точки.
3) Прямая параллельна плоскости, если они...
а) пересекают прямую в одной и той же точке;
б) перпендикулярны одной и той же прямой;
в) удалены от данной точки на равные расстояния;
г) пересекают плоскость в одной точке.
4) Через ... проходит единственная плоскость,
а) две точки; б) три параллельные прямые;
в) три попарно пересекающиеся прямые; г) четыре точки.
5) Прямая пересекает плоскость, если прямая и плоскость .
. .
а) не имеют ни одной общей точки; б) имеют две общие точки;
в) имеют только одну общую точку; г) имеют три общих точки.
6) Если прямая пересекает плоскость квадрата в точке пересечения диагоналей
и перпендикулярна двум смежным его сторонам, то она . . .
а) параллельна двум другим сторонам квадрата;
б) перпендикулярна диагоналям квадрата;
в) параллельна диагоналям квадрата;
г) образует с плоскостью квадрата угол в 30 градусов.
в) имеют только одну общую точку; г) имеют три общих точки.
6) Если прямая пересекает плоскость квадрата в точке пересечения диагоналей
и перпендикулярна двум смежным его сторонам, то она . . .
а) параллельна двум другим сторонам квадрата;
б) перпендикулярна диагоналям квадрата;
в) параллельна диагоналям квадрата;
г) образует с плоскостью квадрата угол в 30 градусов.
Слайд 40
7) Если две параллельные плоскости пересечь третьей, то . . .
а) линии пересечения равны;
б) линии пересечения параллельны;
в) линии пересечения перпендикулярны;
г) плоскости совпадают.
8) Если две параллельные плоскости пересечь двумя параллельными прямыми,
то ...
а) прямые пересекаются в точке;
б) плоскости пересекаются по прямой, параллельной одной из прямых;
в) отрезки, заключенные между плоскостями равны;
г) плоскости перпендикулярны одной из прямых.
9) Перпендикуляром к плоскости называют прямую, . . .
а) пересекающую плоскость;
б) перпендикулярную некоторой прямой в плоскости;
в) перпендикулярную любой прямой в плоскости;
г) лежащую в параллельной плоскости.
а) прямые пересекаются в точке;
б) плоскости пересекаются по прямой, параллельной одной из прямых;
в) отрезки, заключенные между плоскостями равны;
г) плоскости перпендикулярны одной из прямых.
9) Перпендикуляром к плоскости называют прямую, . . .
а) пересекающую плоскость;
б) перпендикулярную некоторой прямой в плоскости;
в) перпендикулярную любой прямой в плоскости;
г) лежащую в параллельной плоскости.
10) Планиметрия - это измерения . . .
а) углов; б) отрезков; в) на плоскости; г) в пространстве.
11) Если две точки прямой принадлежат плоскости, то прямая ...
а) называется проекцией точки на плоскость;
б) лежит в плоскости;
в) пересекает плоскость под прямым углом;
г) называется перпендикуляром к плоскости.
Слайд 4112) Прямые, имеющие одну общую точку называют . . .
а) скрещивающимися; б) пересекающимися; в) параллельными; г) совпадающими.
13) Две плоскости параллельны, если они . . .
а) перпендикулярны одной и той же прямой;
б) параллельны одной и той же прямой;
в) пересекаются в одной точке;
г) пересекают одну и ту же прямую,
14) Если две прямые параллельны третьей, то они . . .
а) перпендикулярны друг другу; б) параллельны между собой;
в) совпадают; г) пересекаются.
15) Если две прямые лежат в разных плоскостях, то они…
а) пересекаются; б) скрещеваются; в) перпендикулярны; г) папраллельны.
15) Если две прямые лежат в разных плоскостях, то они…
а) пересекаются; б) скрещеваются; в) перпендикулярны; г) папраллельны.
НАЗАД
Слайд 42параллельные
пересекающиеся
перпендикулярные
лежит
Имеют множество общих точек
Имеют одну общую точку
Не имеют общих точек
Образуют прямой
угол
Задание 2.
«Взаимное расположение прямой и плоскости»
Составь соответствие.
НАЗАД
Слайд 43Литература
Гусев В. , Кайдасов Ж., Кагабаева А. Геометрия: учебник для 10
класса естественно – математического направления общеобразовательных школ – Алматы: Издательство «Мектеп», 2007 – 96с.
Гусев В. , Кайдасов Ж., Кагабаева А. методическое пособие «Геометрия» для 10 класса естественно – математического направления общеобразовательных школ – Алматы: Издательство «Мектеп», 2007.
Атанасян Л.С., Бутузов В.Ф., Кадомцев С.Б. и др. Геометрия, 10-11: Учеб. для общеобразовательных учреждений. – М.: Просвещение, 2010.
http://window.edu.ru/catalog/resources?p_page=32&p_nr=50
http:// shool-collection.edu
http:// festival.1september.ru
http://yutube.com
Гусев В. , Кайдасов Ж., Кагабаева А. методическое пособие «Геометрия» для 10 класса естественно – математического направления общеобразовательных школ – Алматы: Издательство «Мектеп», 2007.
Атанасян Л.С., Бутузов В.Ф., Кадомцев С.Б. и др. Геометрия, 10-11: Учеб. для общеобразовательных учреждений. – М.: Просвещение, 2010.
http://window.edu.ru/catalog/resources?p_page=32&p_nr=50
http:// shool-collection.edu
http:// festival.1september.ru
http://yutube.com
