- Главная
- Разное
- Образование
- Спорт
- Естествознание
- Природоведение
- Религиоведение
- Французский язык
- Черчение
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, фоны, картинки для презентаций
- Экология
- Экономика
Презентация, доклад на тему Египетский треугольника. Пифагоровы штаны.
Содержание
- 1. Египетский треугольника. Пифагоровы штаны.
- 2. «Пифагоровы штаны» (доказательство Евклида) В
- 3. Доказательство, основанное на использовании понятия равновеликости фигур
- 4. Решение задач по готовым чертежамНайти: 1) АВ;
- 5. Египетский треугольник
- 6. Слайд 6
- 7. Слайд 7
- 8. Слайд 8
- 9. Слайд 9
- 10. Слайд 10
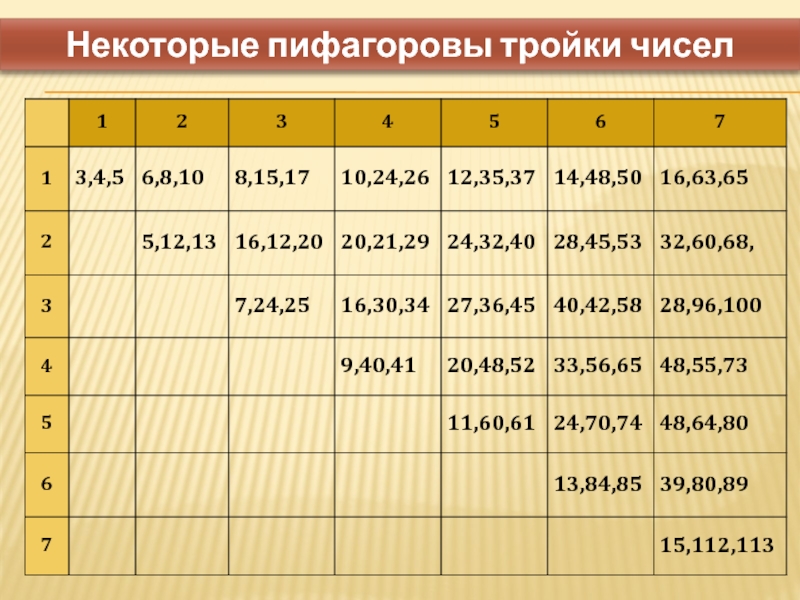
- 11. Некоторые пифагоровы тройки чисел
- 12. Теорема ,обратная теореме Пифагора Теорема. Если квадрат
- 13. 1)В прямоугольном треугольнике катеты равны 1,5 и
- 14. Рефлексия урока- Что нового узнали на уроке?- Какие задания понравились?- Какие задания вызвали затруднения?
«Пифагоровы штаны» (доказательство Евклида) В течение двух тысячелетий применяли доказательство, придуманное Евклидом, которое помещено в его знаменитых «Началах».
Слайд 2 «Пифагоровы штаны» (доказательство Евклида)
В течение двух тысячелетий применяли
доказательство, придуманное Евклидом,
которое помещено в его знаменитых «Началах».
Слайд 3Доказательство, основанное на использовании понятия равновеликости фигур
Древние индусы, которым принадлежит
это рассуждение, обычно не записывали его, а сопровождали чертеж лишь одним словом: «Смотри!». Вполне возможно, что такое же доказательство предложил и Пифагор. рисунке изображено два квадрата. Длина сторон каждого квадрата равна а + в . Каждый из квадратов разбит на части, состоящие из квадратов и прямоугольных треугольников. Ясно, что если от площади квадрата отнять учетверённую площадь прямоугольного треугольника с катетами а, в, то останутся равные площади, т. е. с2 = а2 + в2.
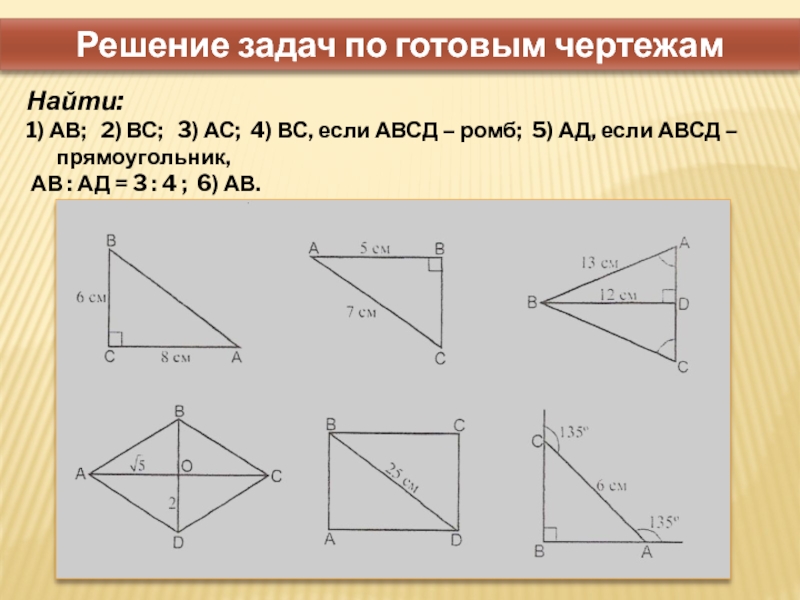
Слайд 4Решение задач по готовым чертежам
Найти:
1) АВ; 2) ВС;
3) АС; 4) ВС, если АВСД – ромб; 5) АД, если АВСД – прямоугольник,
АВ : АД = 3 : 4 ; 6) АВ.
АВ : АД = 3 : 4 ; 6) АВ.
Слайд 12Теорема ,обратная теореме Пифагора
Теорема. Если квадрат одной стороны треугольника равен
сумме квадратов двух других сторон, то треугольник прямоугольный.
Дано : АВС
АВ2 = АС2 + ВС2
Доказать , что С = 90 .
Доказательство :
Пусть в треугольнике АВС АВ2 = АС2 + ВС2. Докажем , что угол С прямой. Рассмотрим прямоугольный треугольник А1 В1 С1 с прямым углом С1 , у которого А1 С1 = АС и В1 С1 = ВС. По теореме Пифагора А1В1 2 = А1С12 + В1С12 , и , значит А1В12 = АС2 + ВС2.
Дано : АВС
АВ2 = АС2 + ВС2
Доказать , что С = 90 .
Доказательство :
Пусть в треугольнике АВС АВ2 = АС2 + ВС2. Докажем , что угол С прямой. Рассмотрим прямоугольный треугольник А1 В1 С1 с прямым углом С1 , у которого А1 С1 = АС и В1 С1 = ВС. По теореме Пифагора А1В1 2 = А1С12 + В1С12 , и , значит А1В12 = АС2 + ВС2.
Но АС 2 + ВС2 = АВ2 по условию теоремы. Следовательно, А1В12 = АВ2 , откуда А1В1 = АВ. Треугольники АВС и А1В1С1 равны по трем сторонам, поэтому угол С равен углу С1, т. е. треугольник АВС прямоугольный с прямым углом С. Теорема доказана
Слайд 131)В прямоугольном треугольнике катеты равны 1,5 и 2. Найдите гипотенузу.
2) В
прямоугольном треугольнике гипотенуза и катет соответственно равны 13 и 5. Найдите второй катет.
3) Определите вид треугольника, стороны которого равны 3, 4 и 5.
3) Определите вид треугольника, стороны которого равны 3, 4 и 5.
Задания:
Слайд 14Рефлексия урока
- Что нового узнали на уроке?
- Какие задания понравились?
- Какие
задания вызвали затруднения?