УЗДЕНОВА Н.М.
- Главная
- Разное
- Образование
- Спорт
- Естествознание
- Природоведение
- Религиоведение
- Французский язык
- Черчение
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, фоны, картинки для презентаций
- Экология
- Экономика
Презентация, доклад на тему Двугранный угол. Признак перпендикулярности плоскостей. Прямоугольный параллелепипед.
Содержание
- 1. Двугранный угол. Признак перпендикулярности плоскостей. Прямоугольный параллелепипед.
- 2. Предполагаемые результаты проекта учащиеся должны
- 3. Основополагающий вопрос Какие свойства у
- 4. Участники проекта 1. Бутова Регина -Двугранный угол
- 5. ДВУГРАННЫЙ УГОЛВыполнила: Бутова Регина
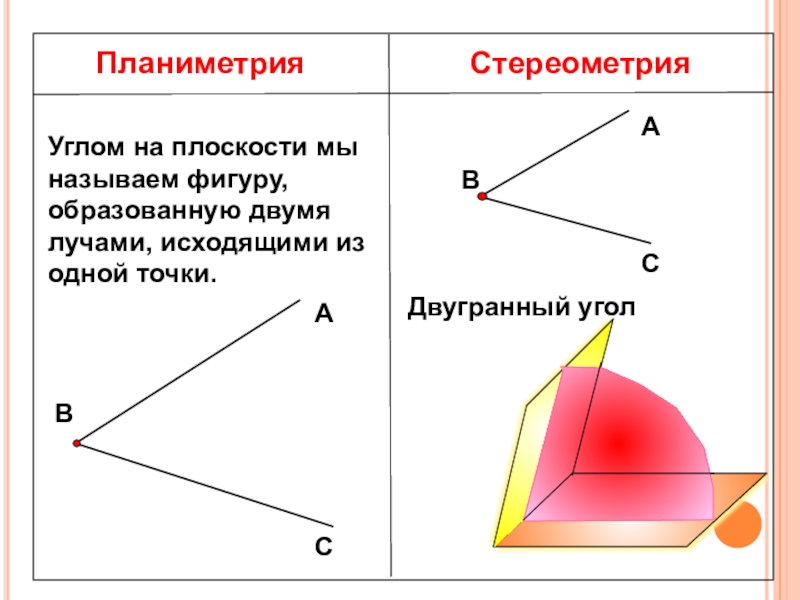
- 6. ПланиметрияСтереометрияУглом на плоскости мы называем фигуру, образованную двумя лучами, исходящими из одной точки.Двугранный угол
- 7. Двугранным углом называется фигура, образованная прямой a
- 8. Угол РDEK Двугранный угол АВNМ, где ВN
- 9. Угол РОК – линейный угол двугранного угла
- 10. Все линейные углы двугранного угла равны друг
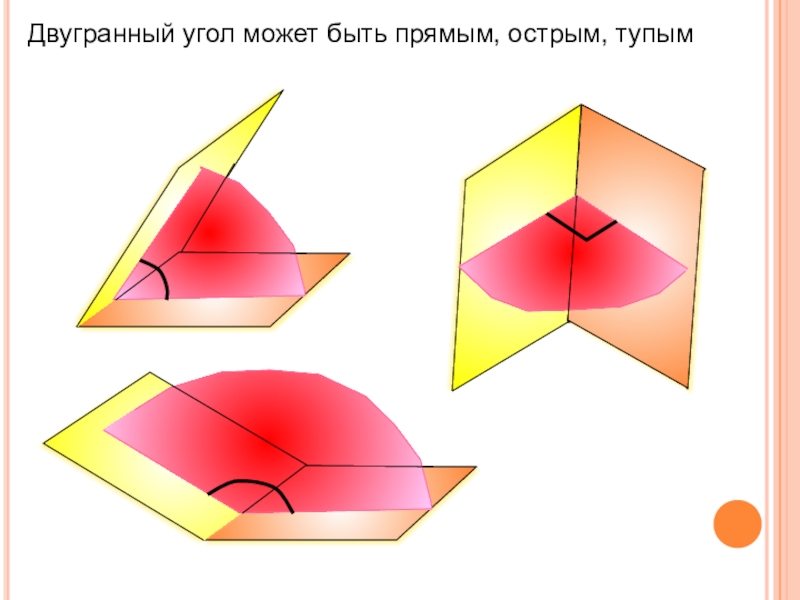
- 11. Двугранный угол может быть прямым, острым, тупым
- 12. ПОСТРОЕНИЕ ЛИНЕЙНОГО УГЛА ДВУГРАННОГО УГЛАВыполнил: Боюнсузов Салауат
- 13. Построить линейный угол двугранного угла ВАСК.Треугольник АВС – равнобедренный.АСВП-рН-яП-яУгол ВMN – линейный угол двугранного угла ВАСКК
- 14. Построить линейный угол двугранного угла ВАСК.Треугольник АВС – прямоугольный.АВП-рН-яП-яУгол ВСN – линейный угол двугранного угла ВАСККС
- 15. Построить линейный угол двугранного угла ВАСК.Треугольник АВС – тупоугольный.АВП-рН-яП-яУгол ВSN – линейный угол двугранного угла ВАСККС
- 16. Построить линейный угол двугранного угла ВDСК.АВСD – прямоугольник.АВП-рН-яП-яУгол ВСN – линейный угол двугранного угла ВDСККСD
- 17. Построить линейный угол двугранного угла ВDСК.АВСD –
- 18. Построить линейный угол двугранного угла ВDСК.АВСD –
- 19. Построить линейный угол двугранного угла ВDСК.АВСD –
- 20. ПРИЗНАК ПЕРПЕНДИКУЛЯРНОСТИ ДВУХ ПЛОСКОСТЕЙВыполнили: Новикова Анастасия
- 21. ПРИЗНАК ПЕРПЕНДИКУЛЯРНОСТИ ДВУХ ПЛОСКОСТЕЙ Определение: Две пересекающиеся
- 22. ПРИЗНАК ПЕРПЕНДИКУЛЯРНОСТИ ДВУХ ПЛОСКОСТЕЙ Теорема: Если одна
- 23. ПРИЗНАК ПЕРПЕНДИКУЛЯРНОСТИ ДВУХ ПЛОСКОСТЕЙ Следствие
- 24. ПРЯМОУГОЛЬНЫЙ ПАРАЛЛЕЛЕПИПЕДВыполнил: Хананов Ренат
- 25. Слайд 25
- 26. ОПРЕДЕЛЕНИЕ. Геометрическое тело или многогранник, состоящий из
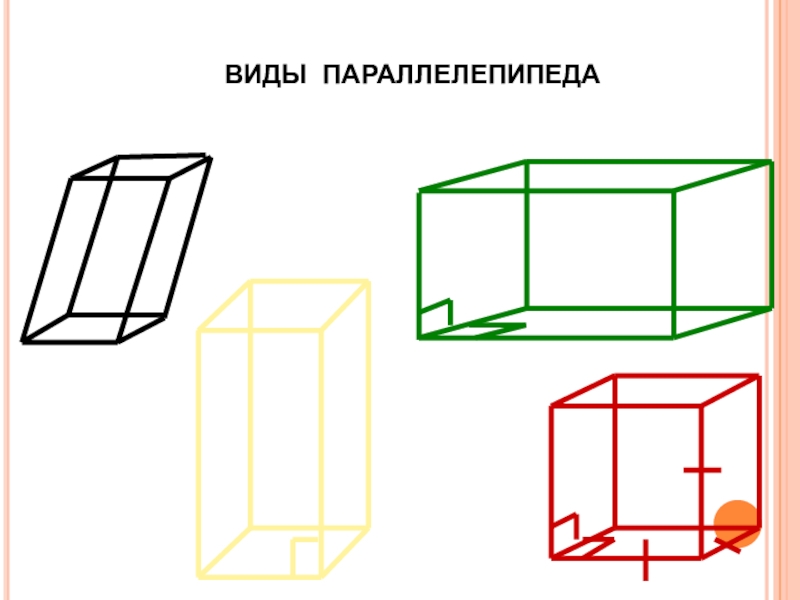
- 27. ВИДЫ ПАРАЛЛЕЛЕПИПЕДА
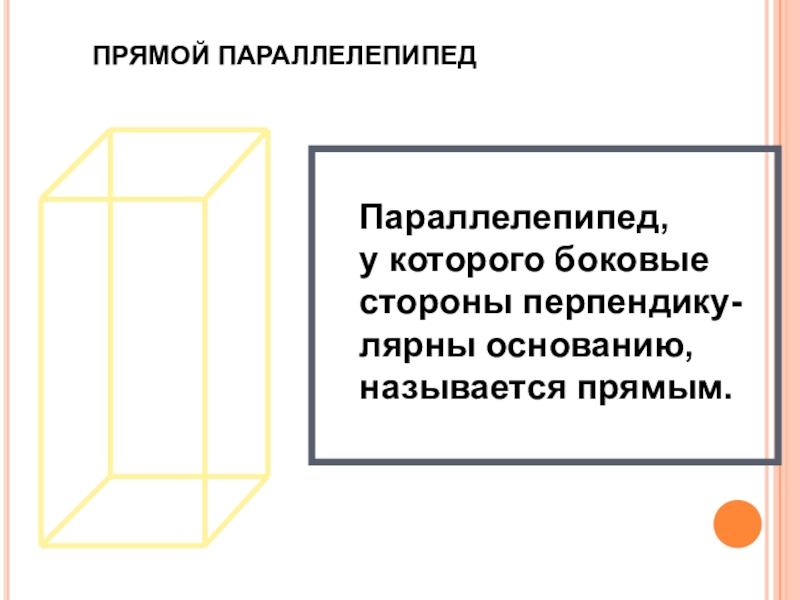
- 28. ПРЯМОЙ ПАРАЛЛЕЛЕПИПЕДПараллелепипед, у которого боковые стороны перпендику-лярны основанию, называется прямым.
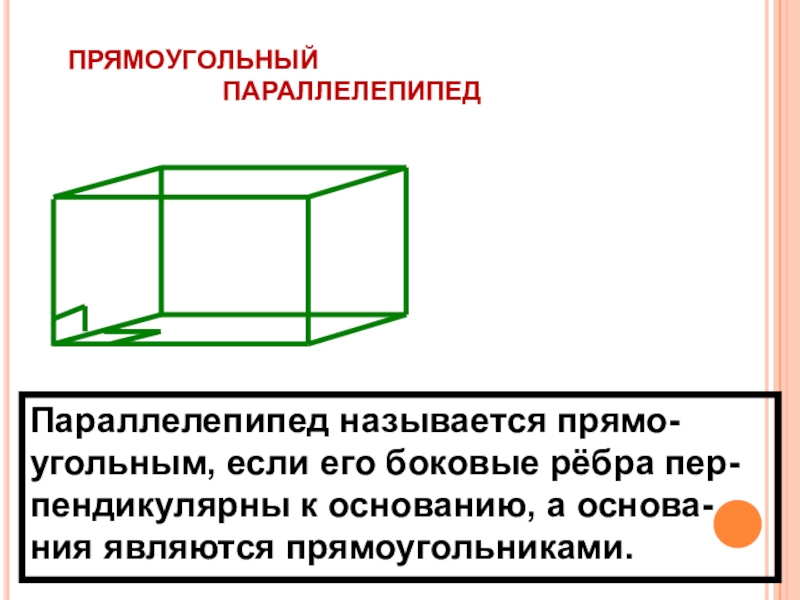
- 29. ПРЯМОУГОЛЬНЫЙ
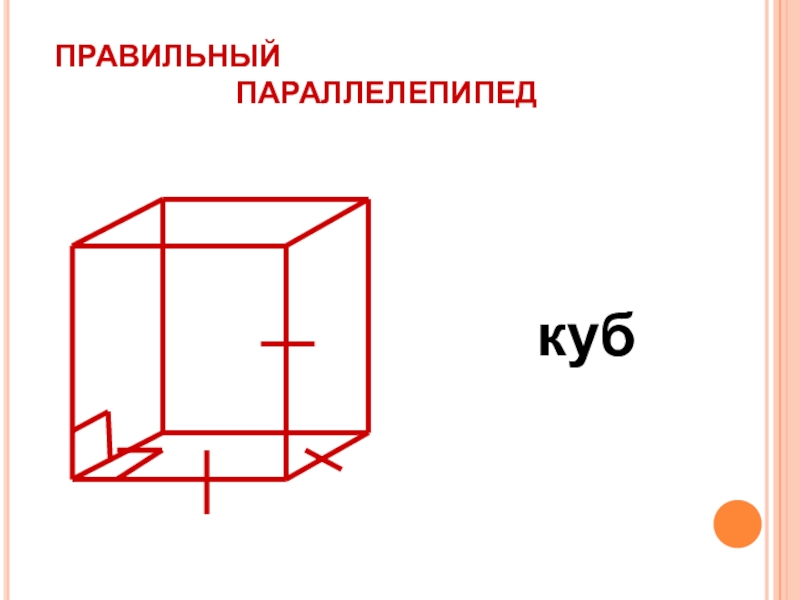
- 30. ПРАВИЛЬНЫЙ ПАРАЛЛЕЛЕПИПЕД куб
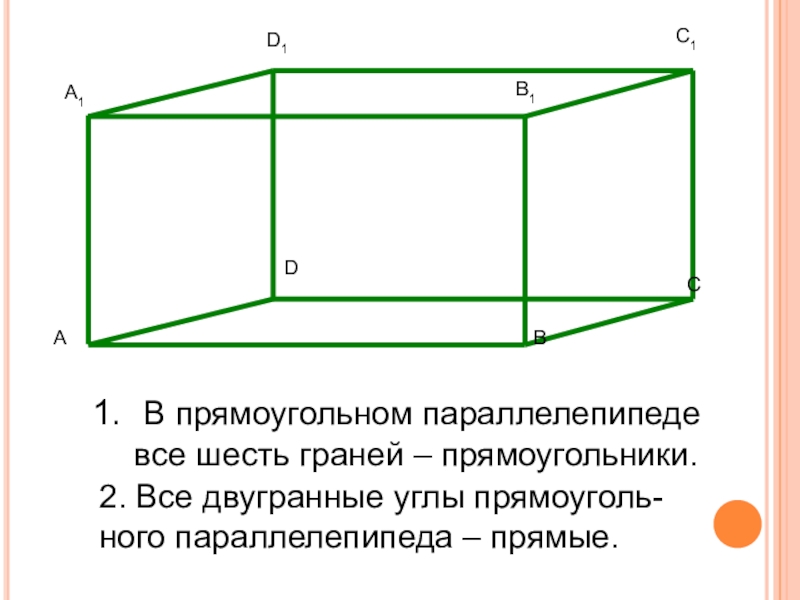
- 31. В прямоугольном параллелепипеде все шесть
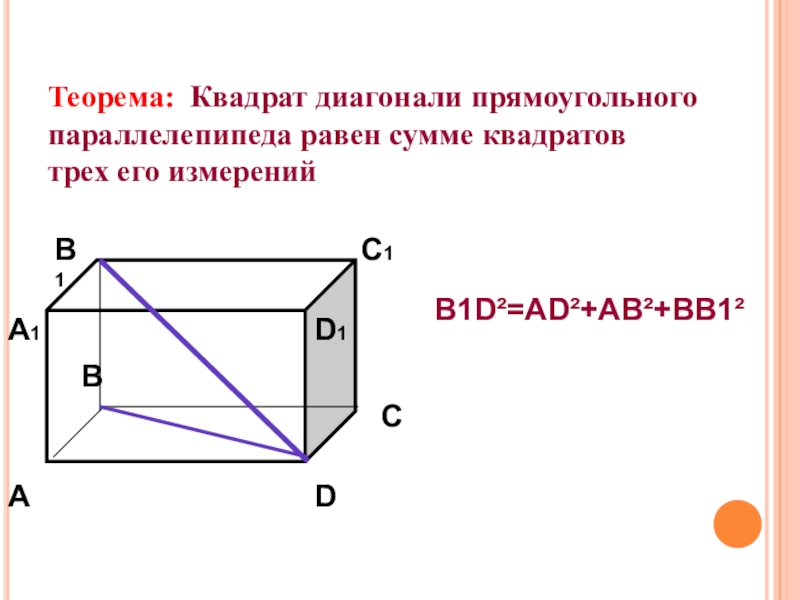
- 32. Теорема: Квадрат диагонали прямоугольного параллелепипеда равен сумме квадратов трех его измеренийАВСDА1В1С1D1B1D²=AD²+AB²+BB1²
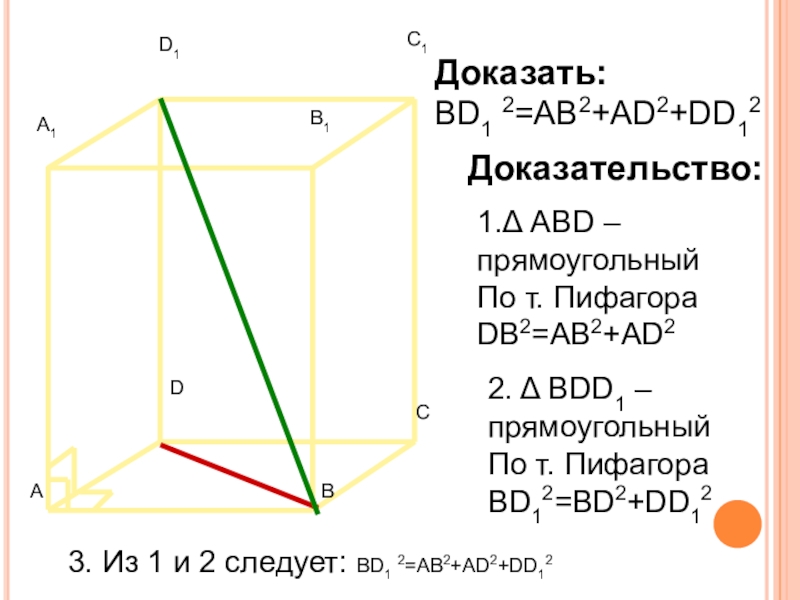
- 33. Доказать:ВD1 2=AB2+AD2+DD12Доказательство:1.Δ ABD –прямоугольныйПо т. ПифагораDB2=AB2+AD22. Δ
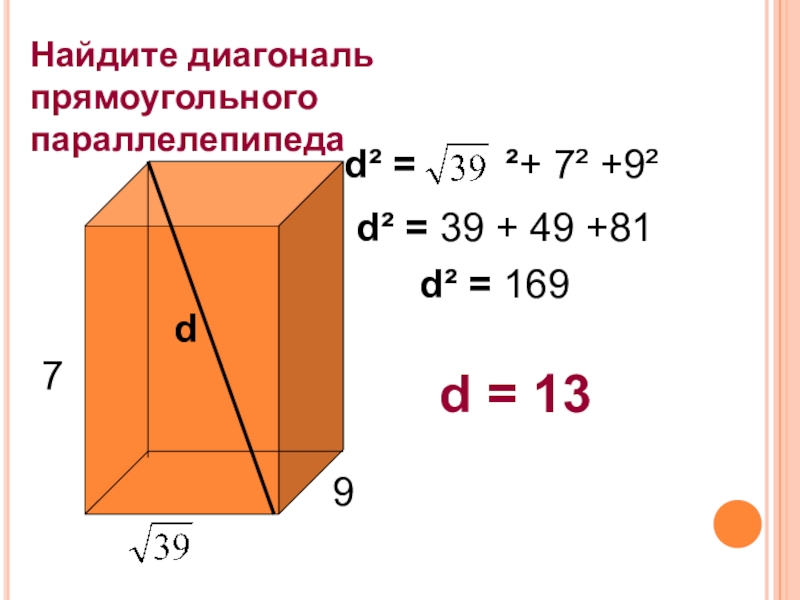
- 34. Найдите диагональ прямоугольного параллелепипеда97dd² =
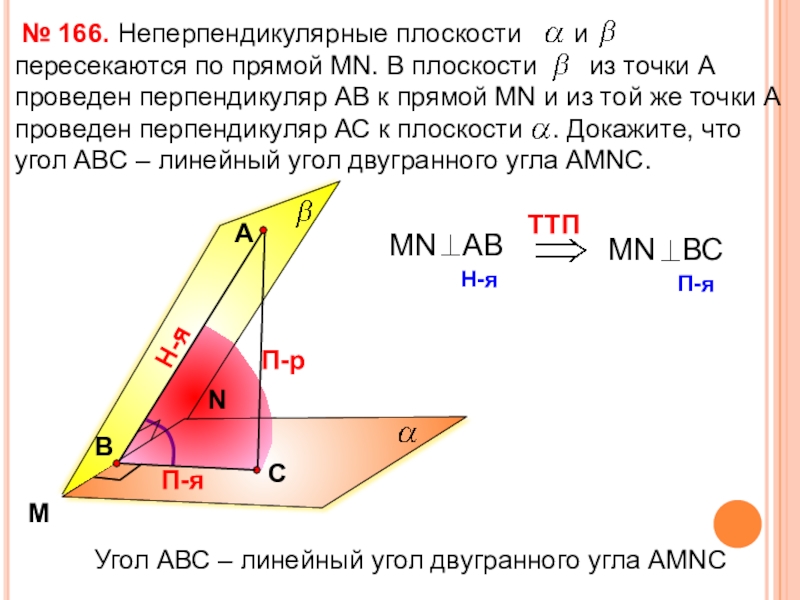
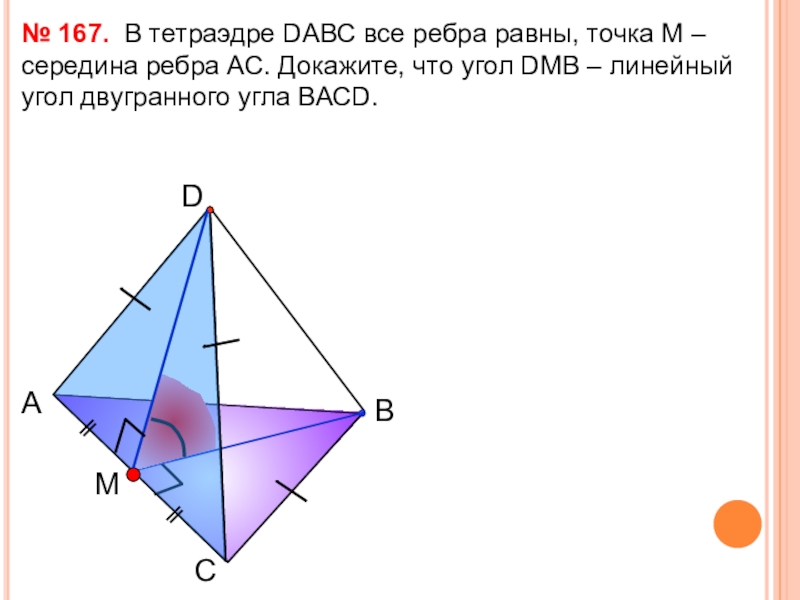
- 35. БАЙРАМКУЛОВА ЭЛЬМИРА – РЕШЕНИЕ ЗАДАЧ №166,167
- 36. № 166.MNАП-рН-яП-яУгол АВС – линейный угол двугранного угла АМNC
- 37. САВDM
- 38. Джанкезов Сослан – решение задач №168,169
- 39. Слайд 39
- 40. Слайд 40
- 41. Предметы, имеющие форму прямоугольного параллелепипеда, имеющие двугранные углы, применяются свойства перпендикулярности плоскостей
- 42. Самостоятельная работа ЗадачаНайти недостающие элементы прямоугольного
- 43. ИТОГИ: ЦЕЛИ И ЗАДАЧИ ПОСТАВЛЕННЫЕ В НАЧАЛЕ
- 44. Генрих Гейне сказал: «В жизни, кроме
- 45. Домашнее задание: п. 22-24, №173, 190
Предполагаемые результаты проекта учащиеся должны знать: 1. Что такое двугранный угол, линейный угол 2. Способы нахождения угла между плоскостями 3. Определение перпендикулярности плоскостей 4. Признаки перпендикулярности плоскостей 5. Понятие прямоугольного параллелепипеда, свойства его граней,
Слайд 1НАЗВАНИЕ ПРОЕКТА :
«ДВУГРАННЫЙ УГОЛ. ПРИЗНАК ПЕРПЕНДИКУЛЯРНОСТИ ПЛОСКОСТЕЙ. ПРЯМОУГОЛЬНЫЙ ПАРАЛЛЕЛЕПИПЕД»
РУКОВОДИТЕЛЬ ПРОЕКТА:
Слайд 2Предполагаемые результаты проекта
учащиеся должны знать:
1. Что такое
двугранный угол, линейный угол
2. Способы нахождения угла между плоскостями
3. Определение перпендикулярности плоскостей
4. Признаки перпендикулярности плоскостей
5. Понятие прямоугольного параллелепипеда, свойства его граней, двугранных углов, диагоналей
6. Применение изученных свойств в решении задач
После завершения проекта учащиеся:
Смогут находить углы между плоскостями
Смогут применять признаки перпендикулярности плоскостей в решении задач
Смогут применять свойства прямоугольного параллелепипеда в жизни
2. Способы нахождения угла между плоскостями
3. Определение перпендикулярности плоскостей
4. Признаки перпендикулярности плоскостей
5. Понятие прямоугольного параллелепипеда, свойства его граней, двугранных углов, диагоналей
6. Применение изученных свойств в решении задач
После завершения проекта учащиеся:
Смогут находить углы между плоскостями
Смогут применять признаки перпендикулярности плоскостей в решении задач
Смогут применять свойства прямоугольного параллелепипеда в жизни
Слайд 3Основополагающий вопрос
Какие свойства у угла и плоскости в
стереометрии через тему «Двугранный угол. Признак перпендикулярности плоскостей. Прямоугольный параллелепипед»
Проблемные вопросы
Определение двугранного угла
Линейного угла
Пересечение плоскостей
Перпендикулярность плоскостей
Прямоугольный параллелепипед
Учебные вопросы
Применение изученных свойств в решении задач
Применение изученных свойств в жизни
Проблемные вопросы
Определение двугранного угла
Линейного угла
Пересечение плоскостей
Перпендикулярность плоскостей
Прямоугольный параллелепипед
Учебные вопросы
Применение изученных свойств в решении задач
Применение изученных свойств в жизни
Слайд 4Участники проекта
1. Бутова Регина -Двугранный угол
2. Боюнсузов Салауат - Построение линейного
угла двугранного угла
3. Новикова Анастасия - Признак перпендикулярности двух плоскостей
4. Хананов Ренат - Прямоугольный параллелепипед
5. Байрамкулова Эльмира – решение задач №166,167
6. Джанкезов Сослан – решение задач №168,169
3. Новикова Анастасия - Признак перпендикулярности двух плоскостей
4. Хананов Ренат - Прямоугольный параллелепипед
5. Байрамкулова Эльмира – решение задач №166,167
6. Джанкезов Сослан – решение задач №168,169
Слайд 6
Планиметрия
Стереометрия
Углом на плоскости мы называем фигуру, образованную двумя лучами, исходящими из
одной точки.
Двугранный угол
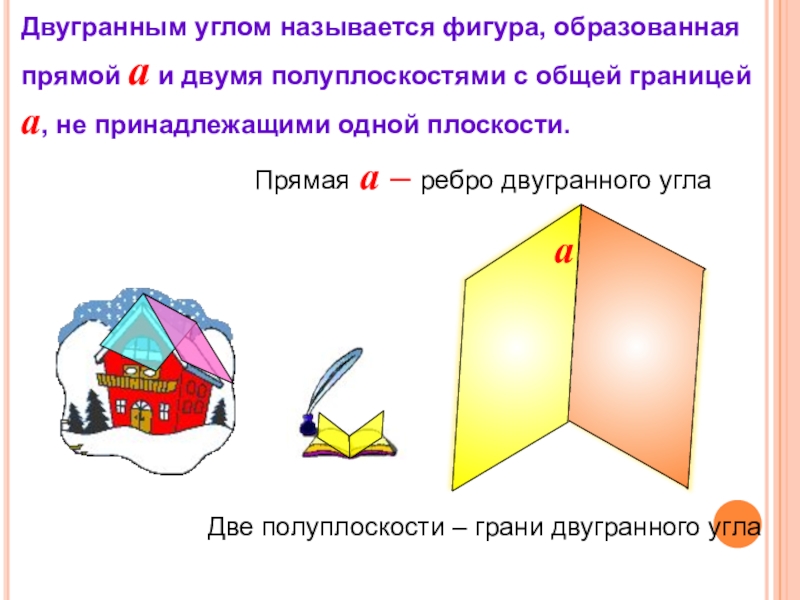
Слайд 7Двугранным углом называется фигура, образованная прямой a и двумя полуплоскостями с
общей границей a, не принадлежащими одной плоскости.
Две полуплоскости – грани двугранного угла
Прямая a – ребро двугранного угла
a
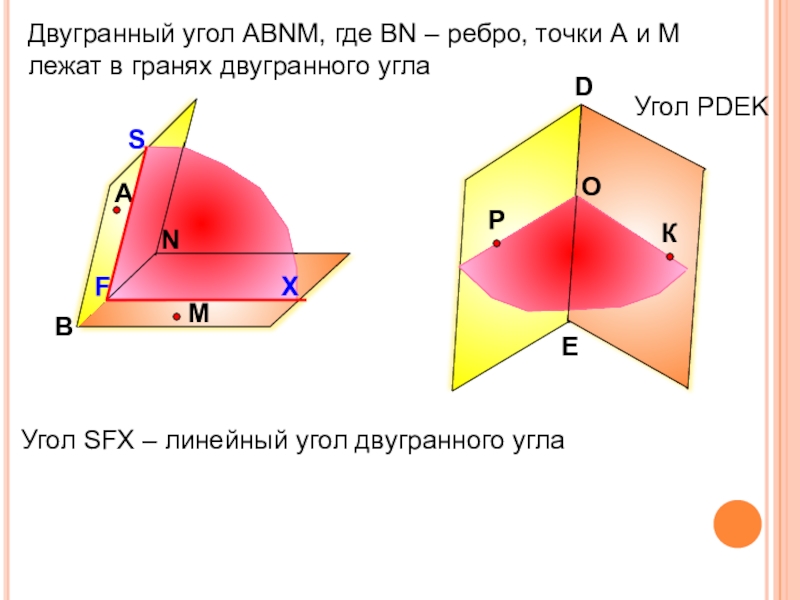
Слайд 8
Угол РDEK
Двугранный угол АВNМ, где ВN – ребро, точки А
и М лежат в гранях двугранного угла
А
В
N
Р
M
К
D
E
Угол SFX – линейный угол двугранного угла
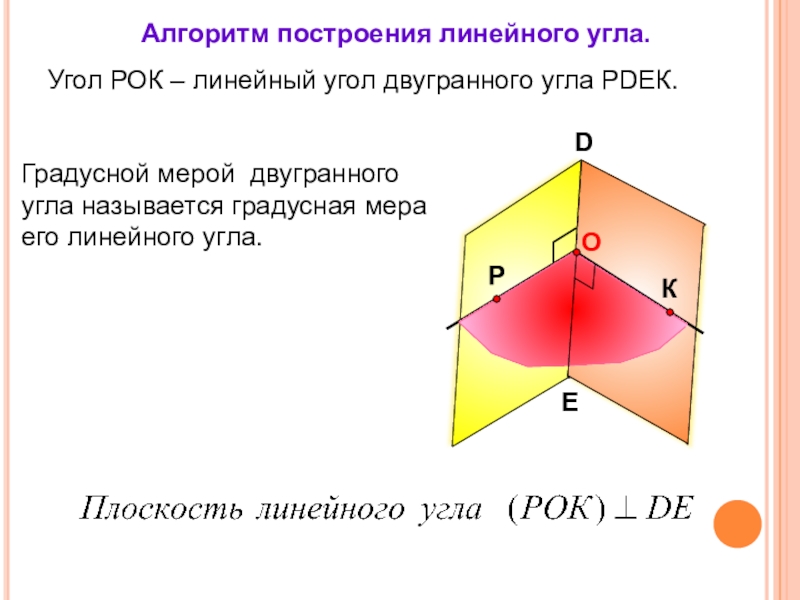
Слайд 9
Угол РОК – линейный угол двугранного угла РDEК.
D
E
Градусной мерой двугранного угла
называется градусная мера его линейного угла.
Алгоритм построения линейного угла.
Слайд 10
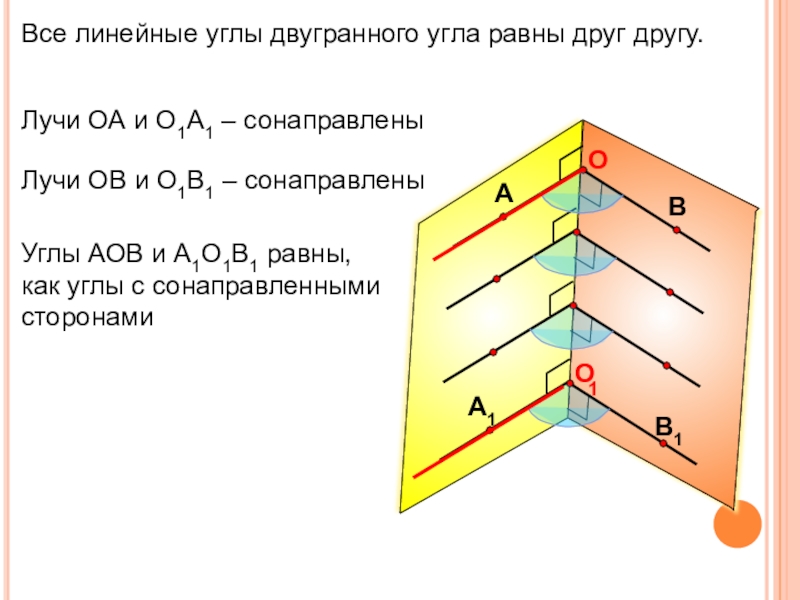
Все линейные углы двугранного угла равны друг другу.
1
Лучи ОА и О1А1
– сонаправлены
Лучи ОВ и О1В1 – сонаправлены
Углы АОВ и А1О1В1 равны,
как углы с сонаправленными сторонами
Слайд 13
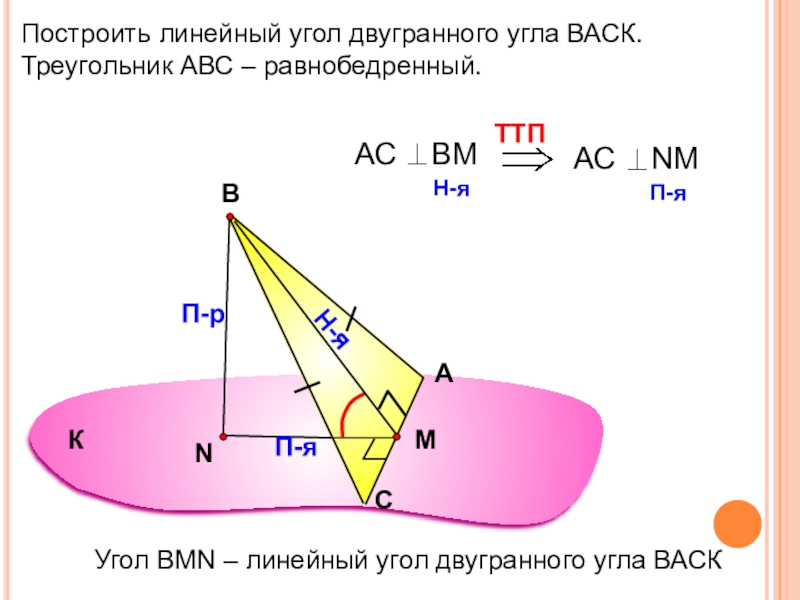
Построить линейный угол двугранного угла ВАСК.
Треугольник АВС – равнобедренный.
А
С
В
П-р
Н-я
П-я
Угол ВMN –
линейный угол двугранного угла ВАСК
К
Слайд 14
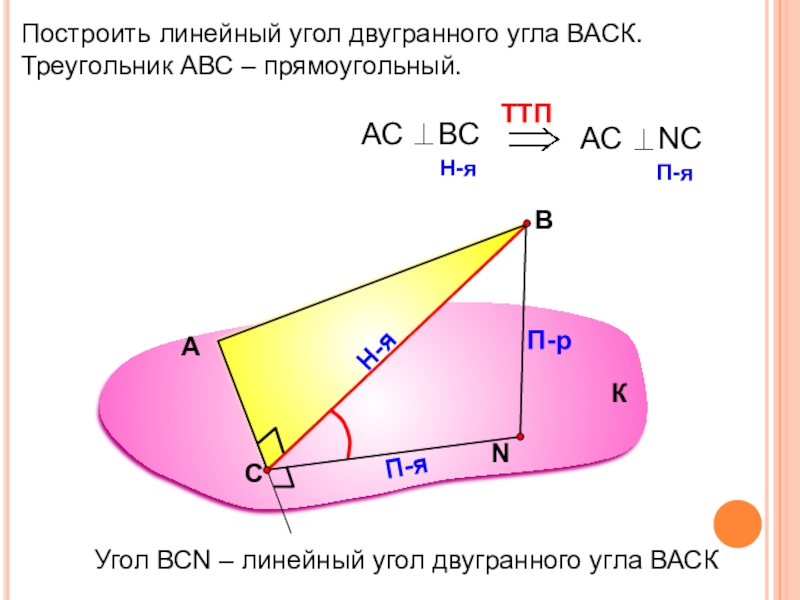
Построить линейный угол двугранного угла ВАСК.
Треугольник АВС – прямоугольный.
А
В
П-р
Н-я
П-я
Угол ВСN –
линейный угол двугранного угла ВАСК
К
С
Слайд 15
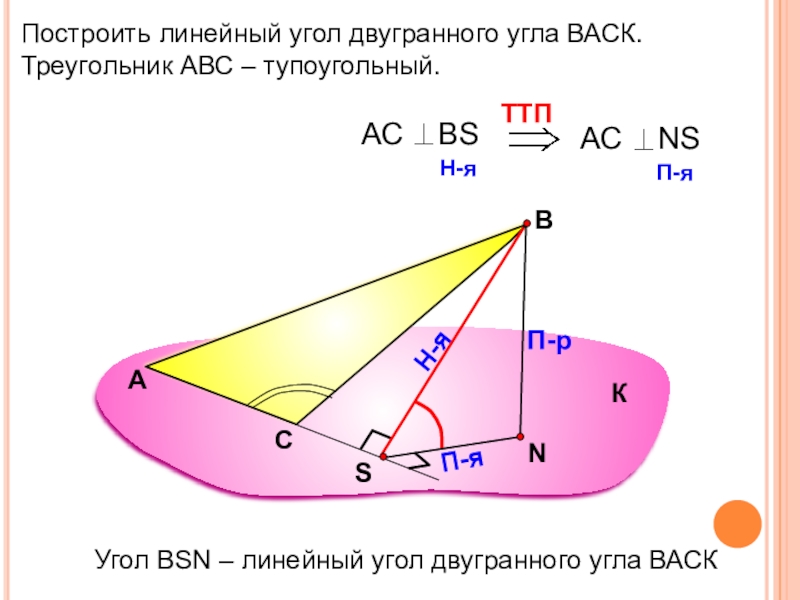
Построить линейный угол двугранного угла ВАСК.
Треугольник АВС – тупоугольный.
А
В
П-р
Н-я
П-я
Угол ВSN –
линейный угол двугранного угла ВАСК
К
С
Слайд 16
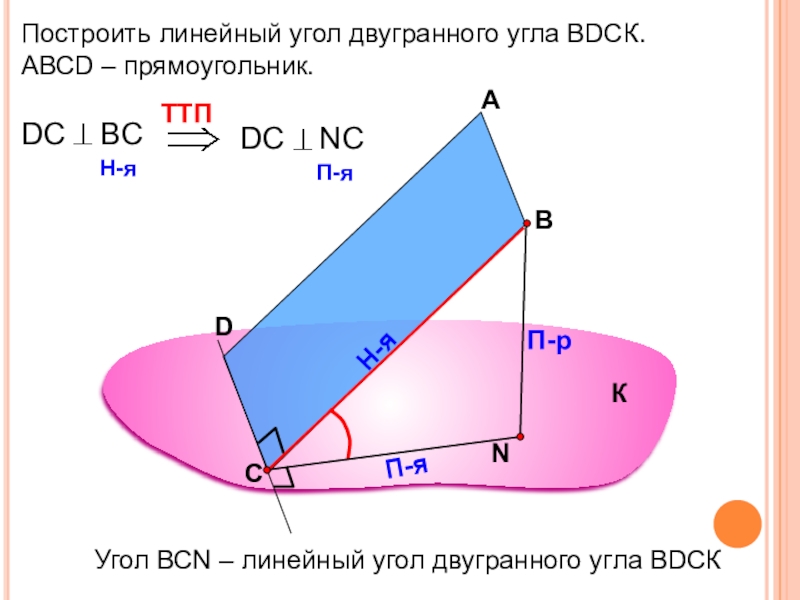
Построить линейный угол двугранного угла ВDСК.
АВСD – прямоугольник.
А
В
П-р
Н-я
П-я
Угол ВСN – линейный
угол двугранного угла ВDСК
К
С
D
Слайд 17
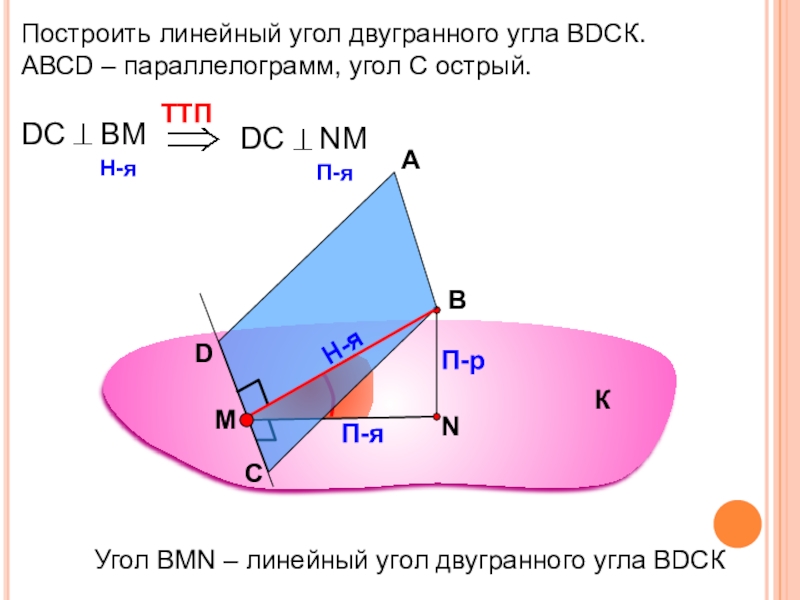
Построить линейный угол двугранного угла ВDСК.
АВСD – параллелограмм, угол С острый.
А
В
П-р
П-я
Угол
ВMN – линейный угол двугранного угла ВDСК
К
С
D
Н-я
Слайд 18
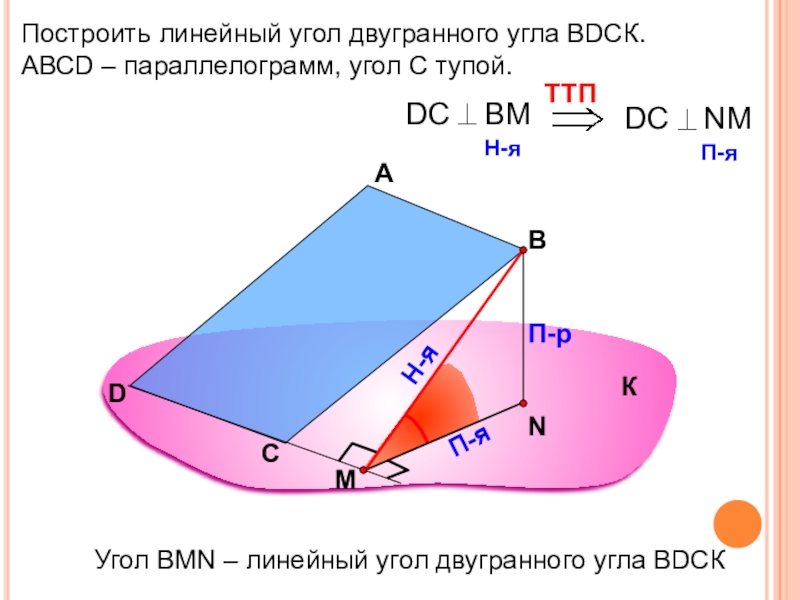
Построить линейный угол двугранного угла ВDСК.
АВСD – параллелограмм, угол С тупой.
А
В
П-р
П-я
Угол
ВMN – линейный угол двугранного угла ВDСК
К
С
D
Н-я
Слайд 19
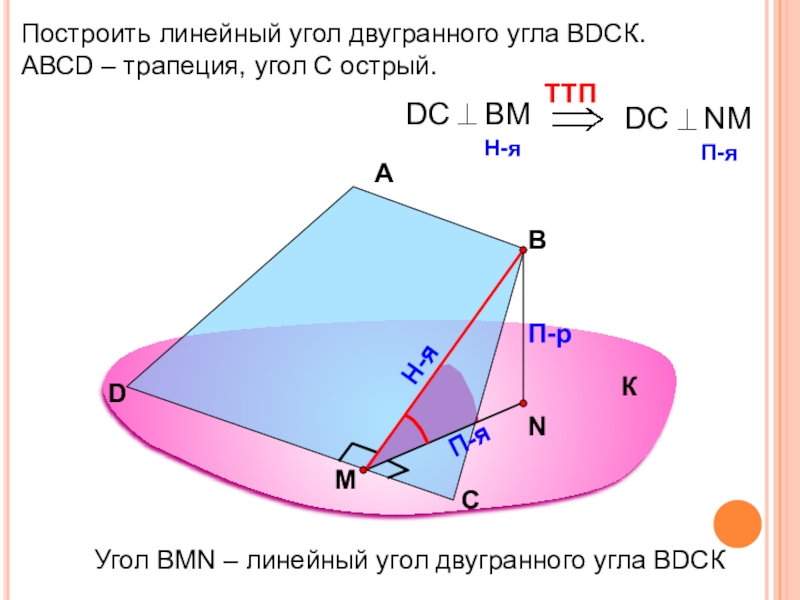
Построить линейный угол двугранного угла ВDСК.
АВСD – трапеция, угол С острый.
А
В
П-р
П-я
Угол
ВMN – линейный угол двугранного угла ВDСК
К
С
D
Н-я
Слайд 21ПРИЗНАК ПЕРПЕНДИКУЛЯРНОСТИ ДВУХ ПЛОСКОСТЕЙ
Определение: Две пересекающиеся плоскости называются перпендикулярными (взаимно
перпендикулярными), если угол между ними равен 900.
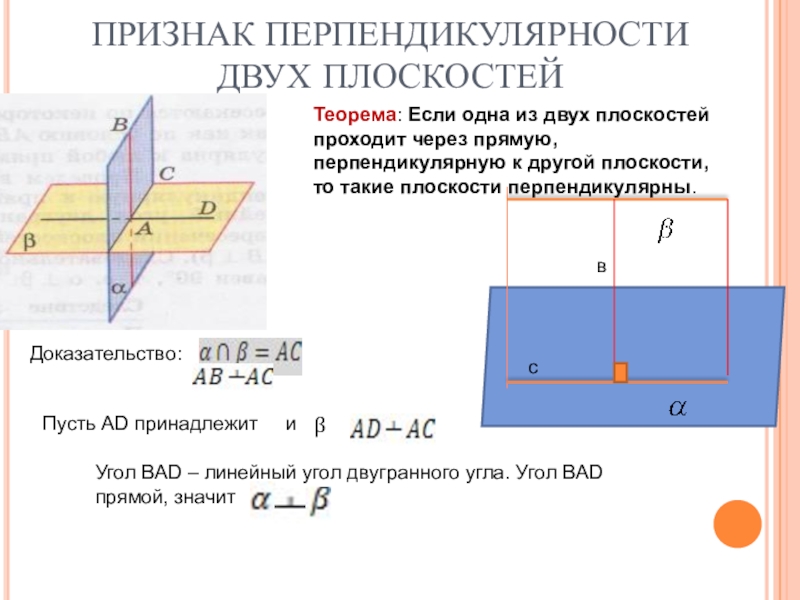
Слайд 22ПРИЗНАК ПЕРПЕНДИКУЛЯРНОСТИ ДВУХ ПЛОСКОСТЕЙ
Теорема: Если одна из двух плоскостей проходит
через прямую, перпендикулярную к другой плоскости, то такие плоскости перпендикулярны.
Доказательство:
Пусть АD принадлежит и
β
Угол ВАD – линейный угол двугранного угла. Угол ВАD прямой, значит
с
в
Слайд 23ПРИЗНАК ПЕРПЕНДИКУЛЯРНОСТИ ДВУХ ПЛОСКОСТЕЙ
Следствие 1: плоскость, перпендикулярная к
ребру двугранного угла, перпендикулярна к его граням.
Следствие 2:
перпендикуляр, проведённый из любой точки одной из двух взаимно перпендикулярных плоскостей к линии их пересечения, есть перпендикуляр к другой плоскости.
Следствие 2:
перпендикуляр, проведённый из любой точки одной из двух взаимно перпендикулярных плоскостей к линии их пересечения, есть перпендикуляр к другой плоскости.
При решении задач используют следующие утверждения
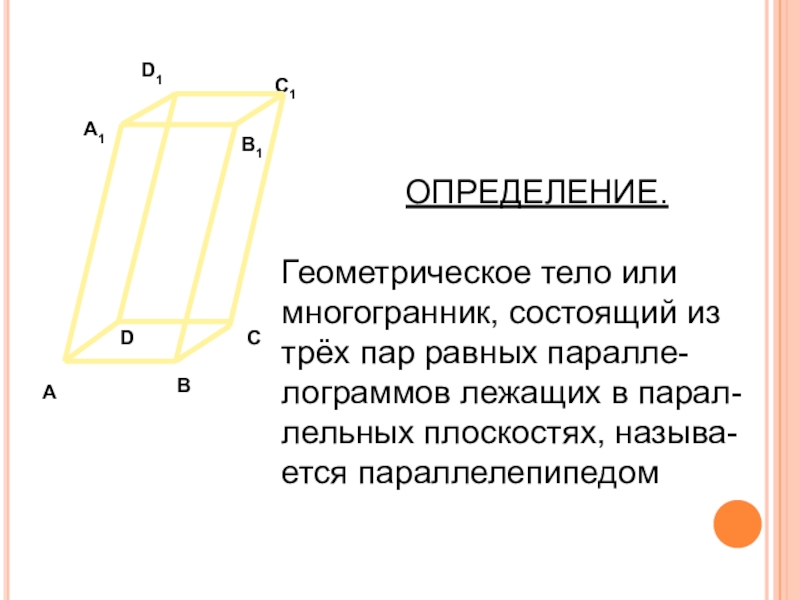
Слайд 26ОПРЕДЕЛЕНИЕ.
Геометрическое тело или многогранник, состоящий из трёх пар равных паралле-
лограммов лежащих в парал-
лельных плоскостях, называ-
ется параллелепипедом
лельных плоскостях, называ-
ется параллелепипедом
Слайд 28ПРЯМОЙ ПАРАЛЛЕЛЕПИПЕД
Параллелепипед,
у которого боковые
стороны перпендику-
лярны основанию,
называется прямым.
Слайд 29ПРЯМОУГОЛЬНЫЙ
ПАРАЛЛЕЛЕПИПЕД
Параллелепипед называется прямо-
угольным, если его боковые рёбра пер- пендикулярны к основанию, а основа- ния являются прямоугольниками.
Слайд 31 В прямоугольном параллелепипеде
все шесть граней – прямоугольники.
2.
Все двугранные углы прямоуголь- ного параллелепипеда – прямые.
Слайд 32Теорема: Квадрат диагонали прямоугольного
параллелепипеда равен сумме квадратов
трех его измерений
А
В
С
D
А1
В1
С1
D1
B1D²=AD²+AB²+BB1²
Слайд 33Доказать:
ВD1 2=AB2+AD2+DD12
Доказательство:
1.Δ ABD –прямоугольный
По т. Пифагора
DB2=AB2+AD2
2. Δ BDD1 –
прямоугольный
По
т. Пифагора
BD12=BD2+DD12
BD12=BD2+DD12
3. Из 1 и 2 следует: ВD1 2=AB2+AD2+DD12
Слайд 34Найдите диагональ прямоугольного
параллелепипеда
9
7
d
d² = ²+ 7² +9²
d² = 39 + 49 +81
d² = 169
d = 13
Слайд 37
С
А
В
D
M
В тетраэдре DАВС все
ребра равны, точка М – середина ребра АС. Докажите, что угол DМВ – линейный угол двугранного угла ВАСD.
№ 167.
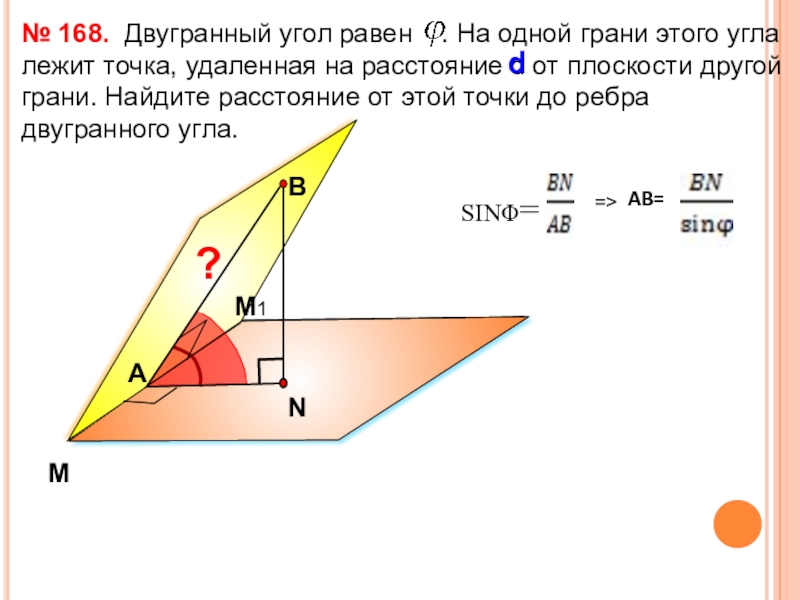
Слайд 39 Двугранный угол равен
. На одной грани этого угла лежит точка, удаленная на расстояние d от плоскости другой грани. Найдите расстояние от этой точки до ребра двугранного угла.
№ 168.
В
d
А
?
М
М1
sinφ=
AB=
=>
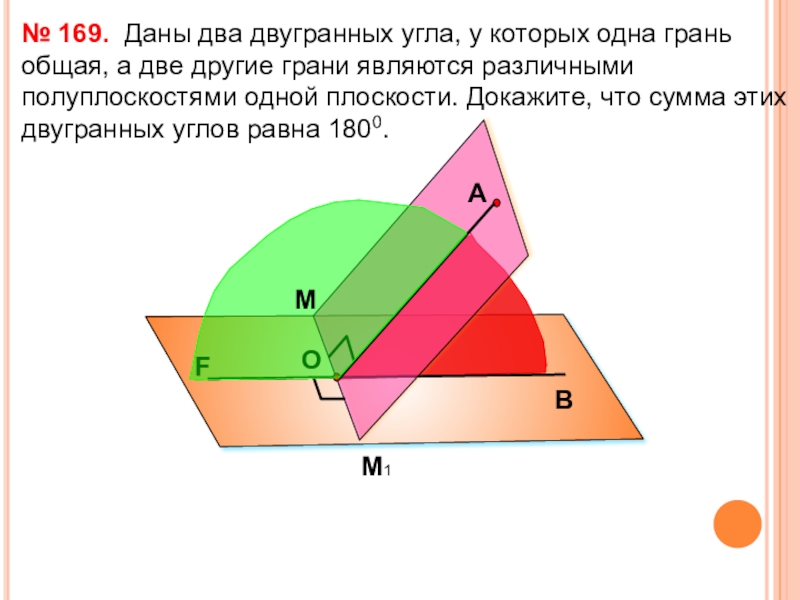
Слайд 40
Даны два двугранных угла,
у которых одна грань общая, а две другие грани являются различными полуплоскостями одной плоскости. Докажите, что сумма этих двугранных углов равна 1800.
№ 169.
А
М
М1
Слайд 41 Предметы, имеющие форму прямоугольного параллелепипеда, имеющие двугранные углы, применяются свойства
перпендикулярности плоскостей
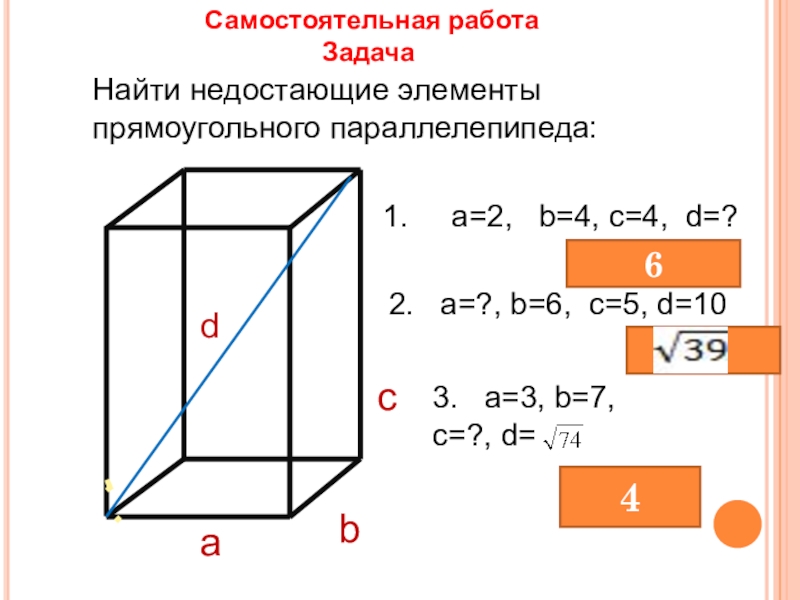
Слайд 42 Самостоятельная работа
Задача
Найти недостающие элементы прямоугольного параллелепипеда:
a
b
c
d
1. a=2,
b=4, c=4, d=?
2. a=?, b=6, c=5, d=10
3. a=3, b=7, c=?, d=
6
4
Слайд 43ИТОГИ:
ЦЕЛИ И ЗАДАЧИ ПОСТАВЛЕННЫЕ В НАЧАЛЕ ПРОЕКТА ДОСТИГНУТЫ
учащиеся узнали:
1. Что
такое двугранный угол, линейный угол
2. Конструктивные способы нахождение угла между плоскостями
3.Определение перпендикулярности плоскостей
4.Признаки перпендикулярности плоскостей
5. Понятие прямоугольного параллелепипеда, свойства его граней, двугранных углов, диагоналей
6. Применение свойств в решении задач
после завершения проекта учащиеся:
Могут находить углы между плоскостями
Могут применять признаки перпендикулярности плоскостей в решении задач
Могут применять свойства прямоугольного параллелепипеда в жизни
2. Конструктивные способы нахождение угла между плоскостями
3.Определение перпендикулярности плоскостей
4.Признаки перпендикулярности плоскостей
5. Понятие прямоугольного параллелепипеда, свойства его граней, двугранных углов, диагоналей
6. Применение свойств в решении задач
после завершения проекта учащиеся:
Могут находить углы между плоскостями
Могут применять признаки перпендикулярности плоскостей в решении задач
Могут применять свойства прямоугольного параллелепипеда в жизни
Слайд 44Генрих Гейне сказал:
«В жизни, кроме здоровья и добродетели, нет
ничего ценнее знания; а его легче всего достигнуть, и дешевле всего добыть: ведь вся работа - это покой, а весь расход – время, которое нам не удержать, даже если мы его не потратим».
