- Главная
- Разное
- Образование
- Спорт
- Естествознание
- Природоведение
- Религиоведение
- Французский язык
- Черчение
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, фоны, картинки для презентаций
- Экология
- Экономика
Презентация, доклад на тему Четыре замечательные точки треугольника
Содержание
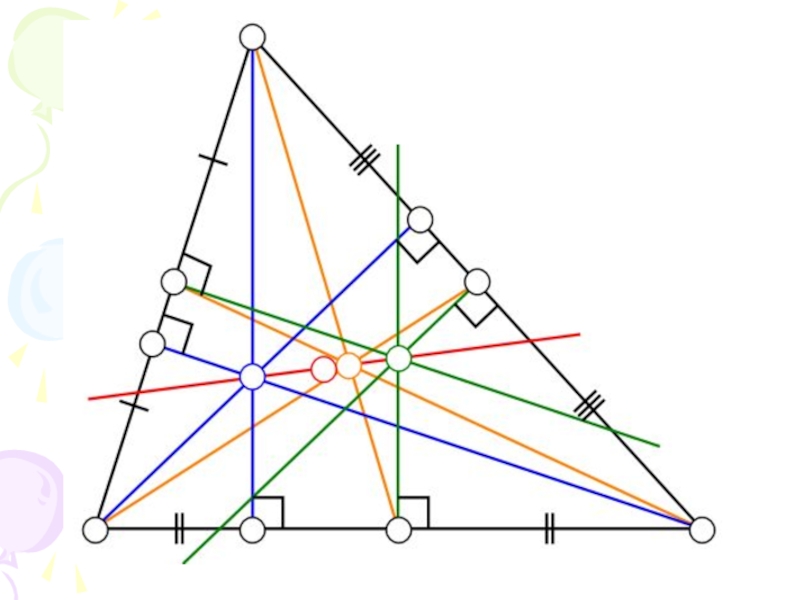
- 1. Четыре замечательные точки треугольника
- 2. Свойство биссектрисы неразвёрнутого углаТеорема1. Каждая точка биссектрисы
- 3. Серединный перпендикуляр к отрезкуТеорема 1. Каждая точка
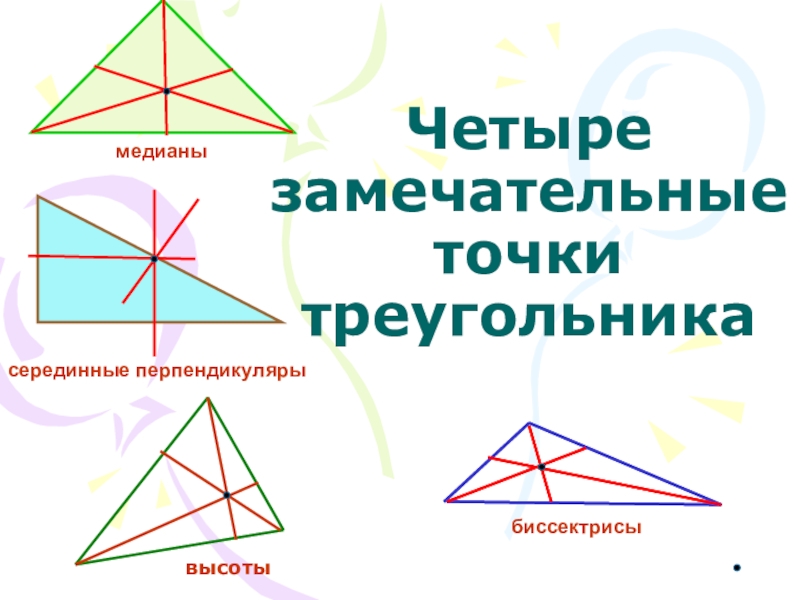
- 4. Четыре замечательные точки треугольникавысотыбиссектрисысерединные перпендикулярымедианы
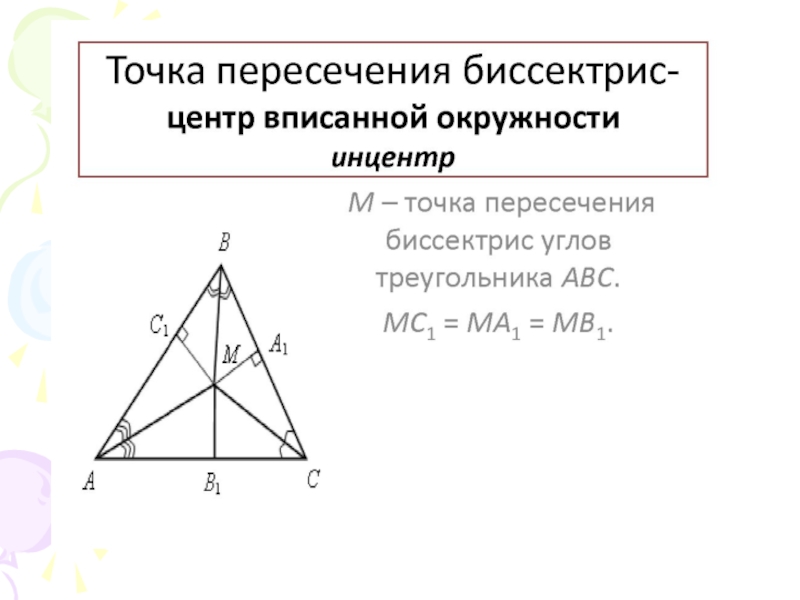
- 5. Первая замечательная точка треугольникаТеорема. Биссектрисы треугольника
- 6. Слайд 6
- 7. Слайд 7
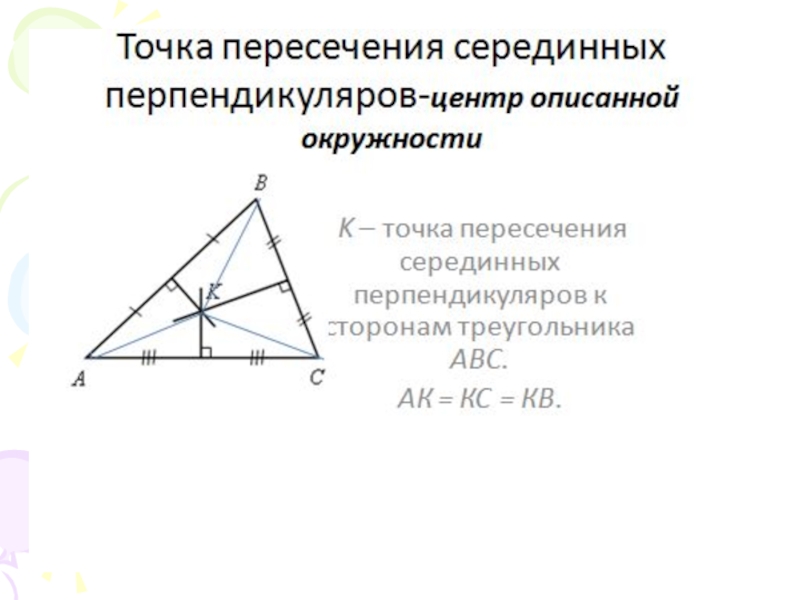
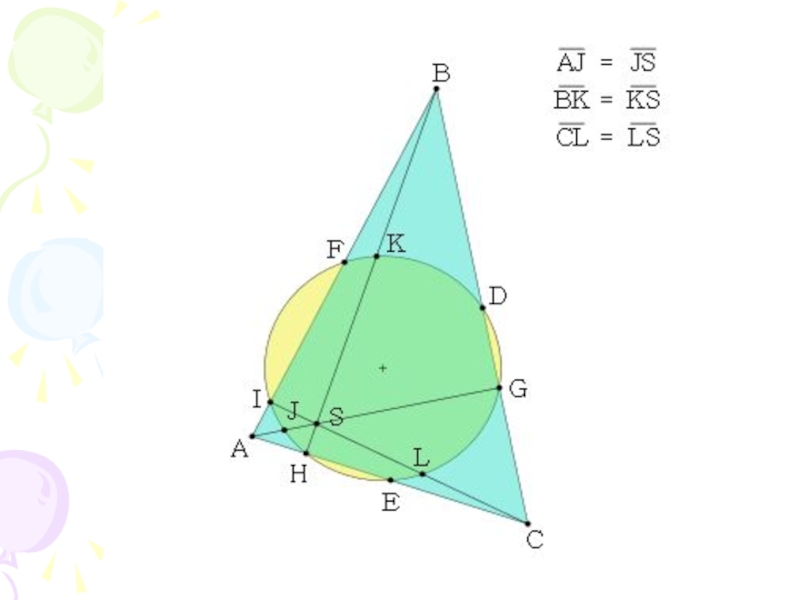
- 8. Вторая замечательная точка треугольникаТеорема. Серединные перпендикуляры
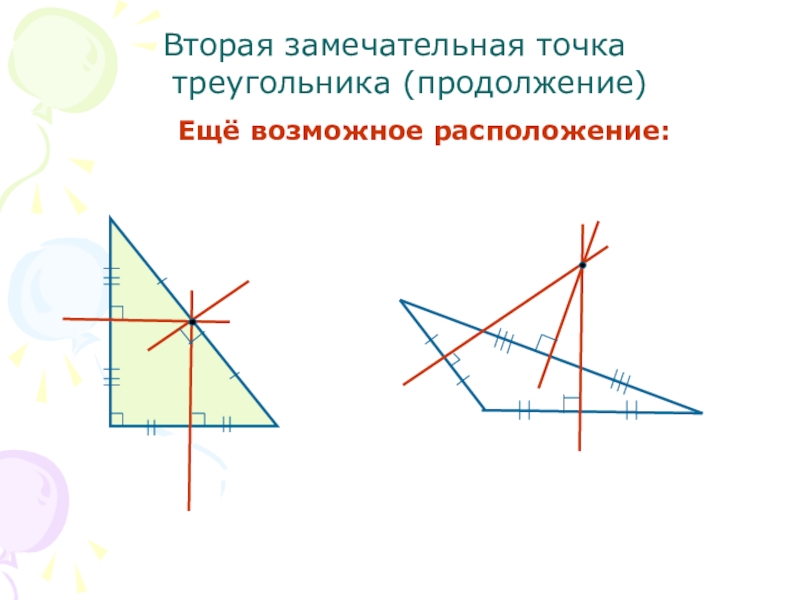
- 9. Вторая замечательная точка треугольника (продолжение)Ещё возможное расположение:
- 10. Слайд 10
- 11. Слайд 11
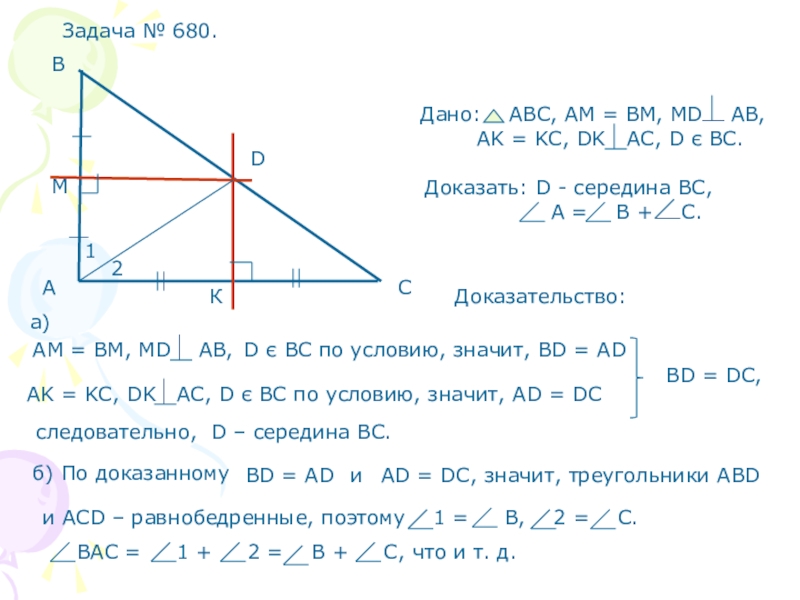
- 12. Доказательство:следовательно, D – середина ВС.
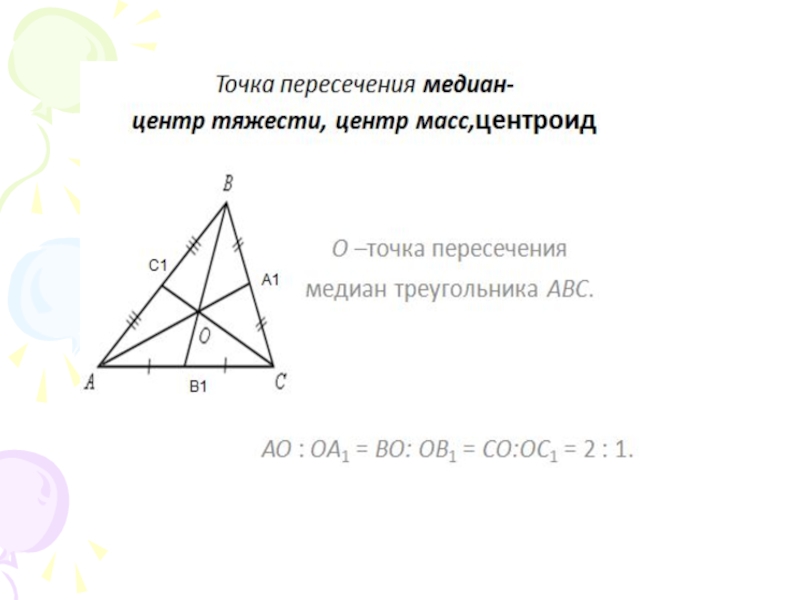
- 13. Третья замечательная точка треугольникаТеорема. Медианы треугольника
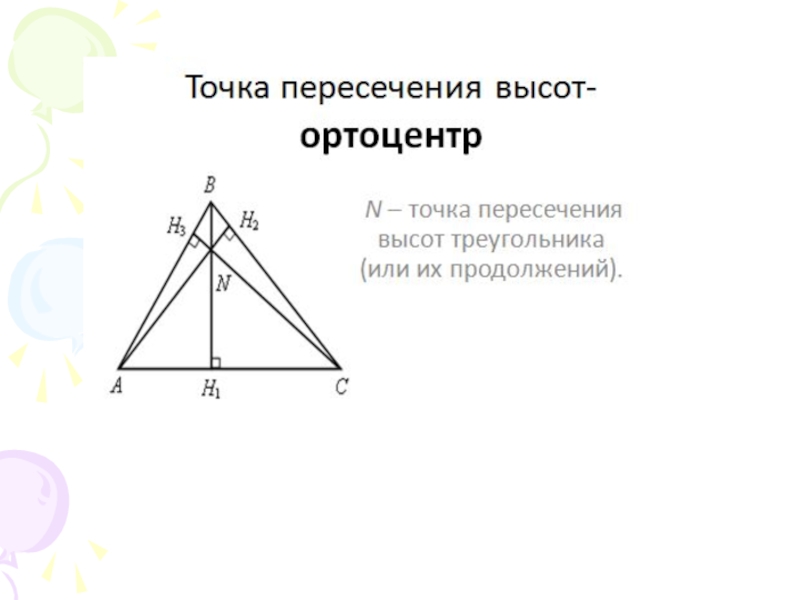
- 14. Четвёртая замечательная точка треугольникаТеорема. Высоты треугольника
- 15. Доказательство:Получим: АСВЕ – параллелограмм, значит, АС =
- 16. Слайд 16
- 17. Слайд 17
- 18. Слайд 18
- 19. Слайд 19
- 20. Слайд 20
- 21. Слайд 21
Слайд 1Презентация к уроку «Четыре замечательные точки треугольника»
Выполнила О.А.Зуева,
Учитель математики
МКОУ СОШ
2012-2013 учебный год
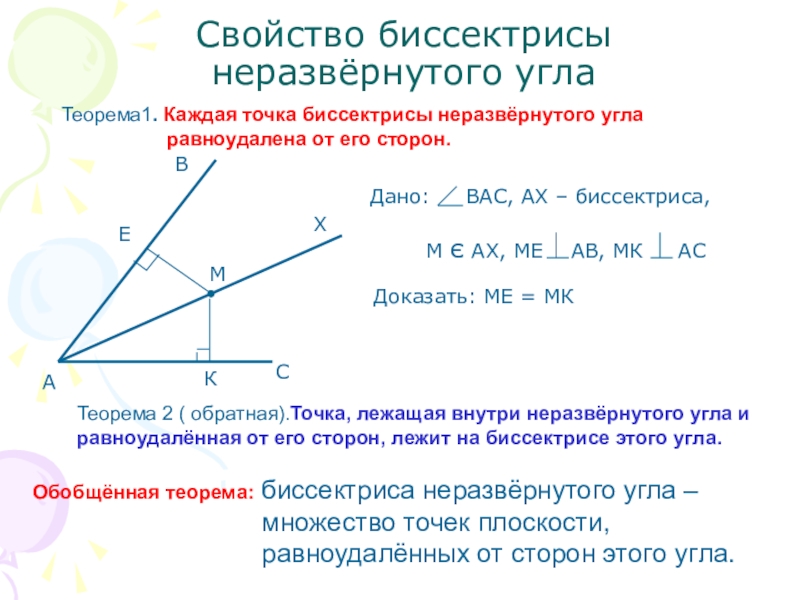
Слайд 2Свойство биссектрисы неразвёрнутого угла
Теорема1. Каждая точка биссектрисы неразвёрнутого угла
Доказать: МЕ = МК
Теорема 2 ( обратная).Точка, лежащая внутри неразвёрнутого угла и равноудалённая от его сторон, лежит на биссектрисе этого угла.
Обобщённая теорема: биссектриса неразвёрнутого угла –
множество точек плоскости,
равноудалённых от сторон этого угла.
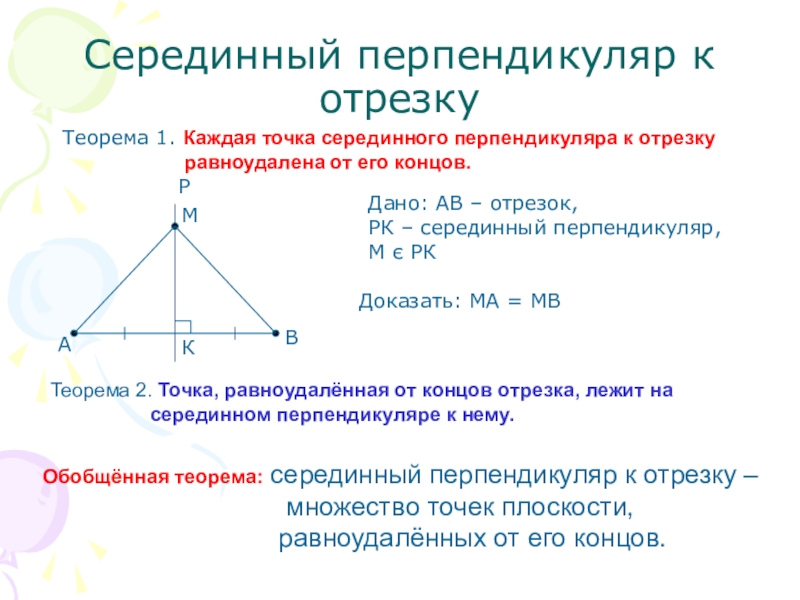
Слайд 3Серединный перпендикуляр к отрезку
Теорема 1. Каждая точка серединного перпендикуляра к отрезку
Дано: АВ – отрезок,
РК – серединный перпендикуляр,
М є РК
Доказать: МА = МВ
Теорема 2. Точка, равноудалённая от концов отрезка, лежит на
серединном перпендикуляре к нему.
Обобщённая теорема: серединный перпендикуляр к отрезку –
множество точек плоскости,
равноудалённых от его концов.
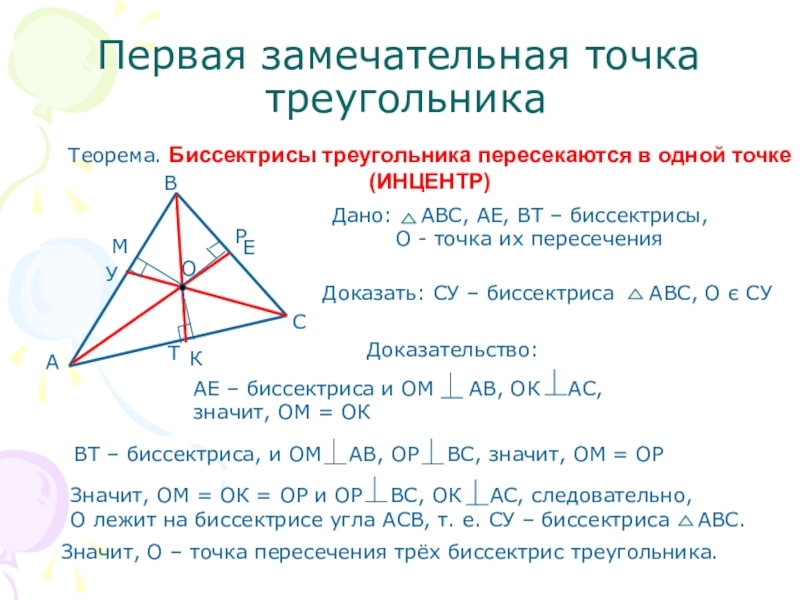
Слайд 5Первая замечательная точка
треугольника
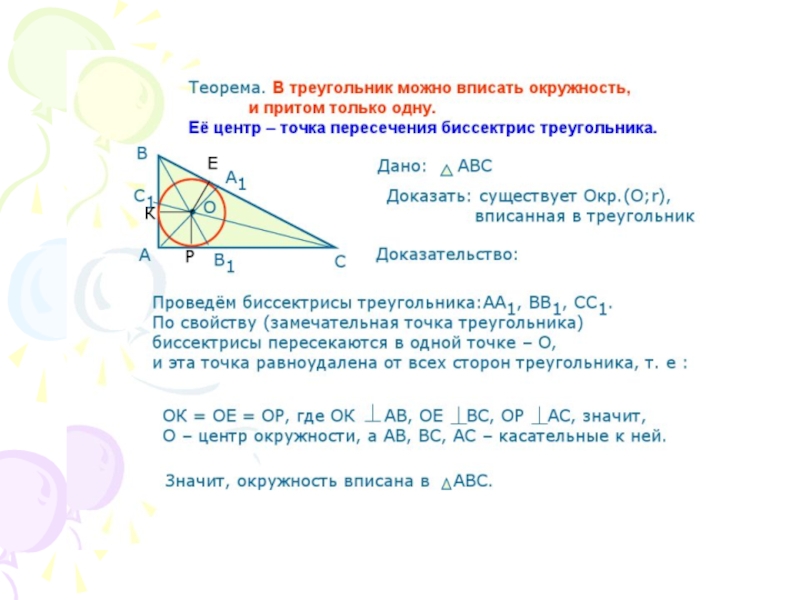
Теорема. Биссектрисы треугольника пересекаются в одной точке
(ИНЦЕНТР)
Доказательство:
Значит, О
Слайд 8Вторая замечательная точка
треугольника
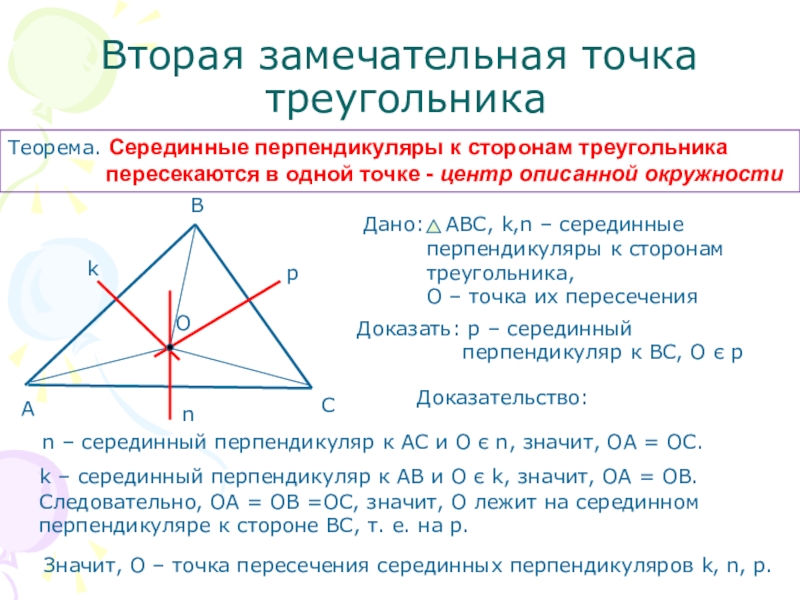
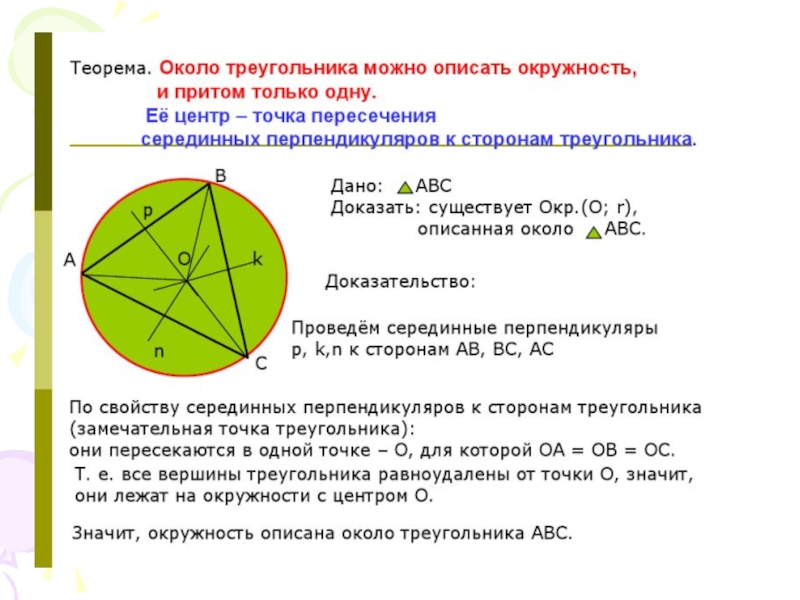
Теорема. Серединные перпендикуляры к сторонам треугольника
Доказать: р – серединный
перпендикуляр к ВС, О є р
Доказательство:
n – серединный перпендикуляр к АС и О є n, значит, ОА = ОС.
k – серединный перпендикуляр к АВ и О є k, значит, ОА = ОВ.
Следовательно, ОА = ОВ =ОС, значит, О лежит на серединном
перпендикуляре к стороне ВС, т. е. на р.
Значит, О – точка пересечения серединных перпендикуляров k, n, p.
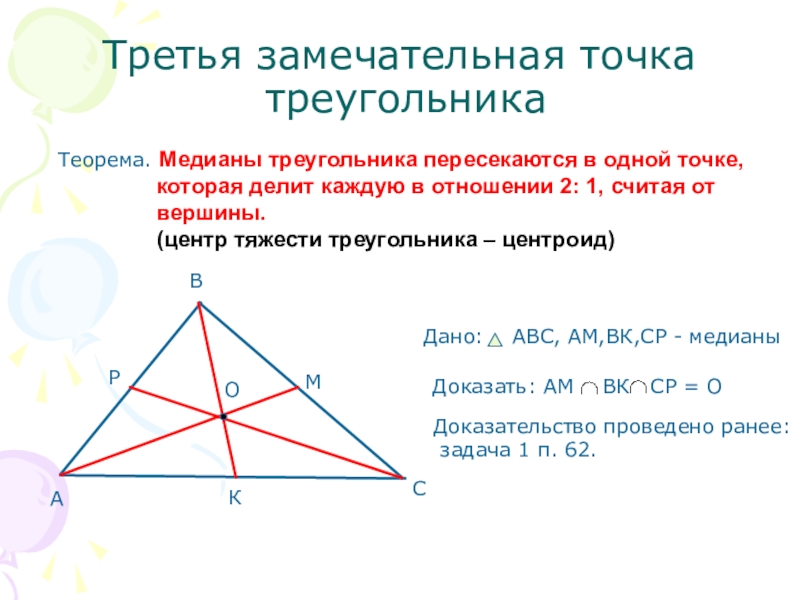
Слайд 13Третья замечательная точка
треугольника
Теорема. Медианы треугольника пересекаются в одной точке,
вершины.
(центр тяжести треугольника – центроид)
Доказательство проведено ранее:
задача 1 п. 62.
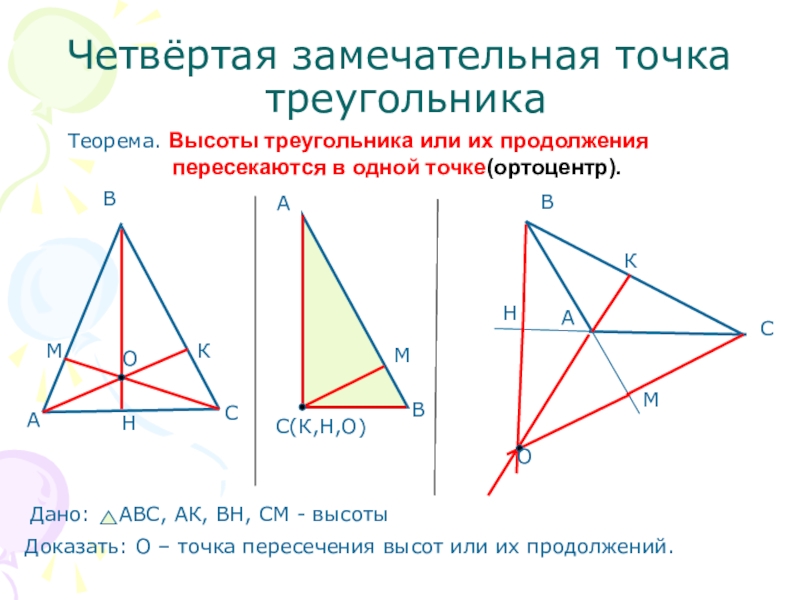
Слайд 14Четвёртая замечательная точка
треугольника
Теорема. Высоты треугольника или их продолжения
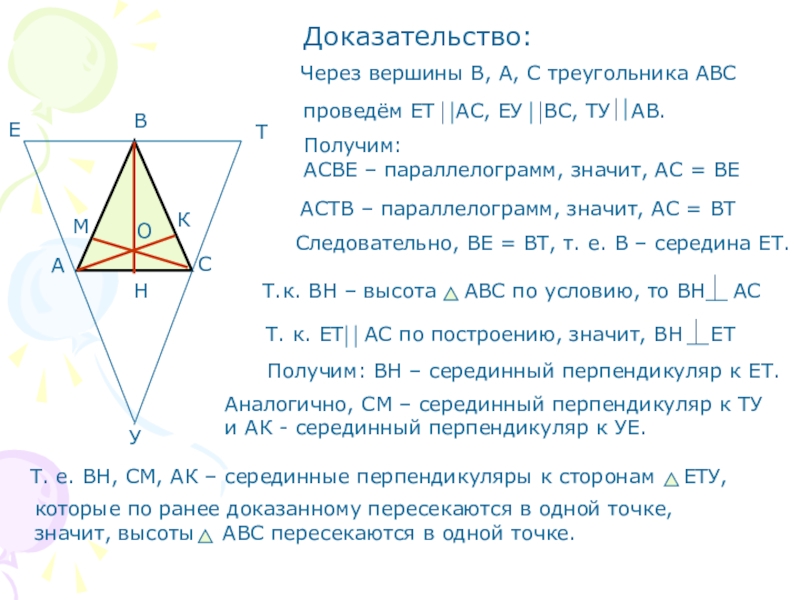
Слайд 15Доказательство:
Получим:
АСВЕ – параллелограмм, значит, АС = ВЕ
АСТВ – параллелограмм, значит,
Следовательно, ВЕ = ВТ, т. е. В – середина ЕТ.
Получим: ВН – серединный перпендикуляр к ЕТ.
Аналогично, СМ – серединный перпендикуляр к ТУ
и АК - серединный перпендикуляр к УЕ.