ГБОУ СОШ с. Камышла
- Главная
- Разное
- Образование
- Спорт
- Естествознание
- Природоведение
- Религиоведение
- Французский язык
- Черчение
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, фоны, картинки для презентаций
- Экология
- Экономика
Презентация, доклад на тему Занимательная и полезная математика
Содержание
- 1. Занимательная и полезная математика
- 2. Введение: О математике мы узнаем с самого
- 3. Цель и задачи. Цель проекта: Показать, что
- 4. Гипотеза и актуальность. Гипотеза:Мой проект изменит отношение
- 5. Историческая справка.Яков Исидорович Перельман – российский, советский
- 6. Создание нового жанра уже само по себе
- 7. История возникновения науки «математика»Слово "математика" происходит от
- 8. Оптические иллюзии.Оптических иллюзий существует очень много. Приведу
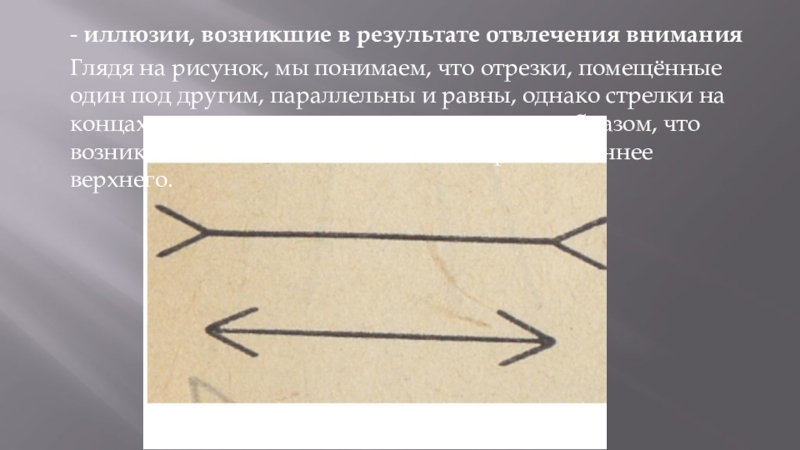
- 9. - иллюзии, возникшие в результате отвлечения вниманияГлядя
- 10. иллюзии, вызванные нарушением ритма. Пример с
- 11. Гексафлексагоны.Никто не станет отрицать, что флексагоны –
- 12. Это произошло в конце 1939 года. Как-то
- 13. Софизмы и парадоксы. И.П. Натансон так определил
- 14. Примеры софизмов. Алгебраический софизм Примером более
- 15. Пример парадокса.Как-то раз хозяину одной великолепной гостиницы
- 16. Невозможные фигуры.В 1954 году Роджер и Лайонел
- 17. В этой статье невозможный треугольник был представлен
- 18. Интересные задачи на логику и не только.
- 19. Слайд 19
- 20. В стозначном числе 12345678901234567890…1234567890 вычеркнули все
- 21. Каким образом можно принести из реки
- 22. Социологический опрос.Я решил провести опрос сверстников с
- 23. Слайд 23
- 24. Слайд 24
- 25. ВыводВыполняя эту исследовательскую работу, я проанализировал и
- 26. Список использованной литературы.Список использованной литературы:https://bp21.livejournal.com/103607.htmlhttps://ru.wikipedia.orghttp://yun.moluch.ru/archive/9/639/https://e-libra.ru/read/253322-matematicheskie-golovolomki-i-razvlecheniya.htmlhttp://bookre.org/reader?file=790836&pg=1
Слайд 1«Занимательная и полезная математика»
Руководитель проекта:
Рахметуллина А. Ш.
Работу выполнил ученик 7Б класса
Слайд 2Введение:
О математике мы узнаем с самого рождения. Ребенок только родился,
В жизни мы постоянно используем математику, например, когда идем в магазин за покупками. Нам нужно все правильно подсчитать, чтобы нам хватило денег.
Математика — это фундаментальная наука, методы которой активно применяются во многих естественных дисциплинах, она также необходима во многих профессиях.
Математика нужна не только в профессии, но также и в повседневной жизни, например, когда мама готовит обед или ужин, она подсчитывает сколько грамм ей нужно сахара или муки. Тут она тоже применяет математические вычисления.
Слайд 3Цель и задачи.
Цель проекта:
Показать, что математику надо рассматривать не
Задачи:
- познакомить одноклассников с популяризатором физики, математики и астрономии, с одним из основоположников жанра научно-популярной литературы и основоположником занимательной науки Я.И. Перельманом;
- найти материал по математике в интернете, интересный для сверстников: о иллюзиях, гексафлексагонах, софизмах и парадоксах;
- создать свой собственный банк задач повышенного уровня сложности или на логическое мышление;
- провести социологический опрос.
Слайд 4Гипотеза и актуальность.
Гипотеза:
Мой проект изменит отношение сверстников к предмету математика.
Математика всегда вокруг нас, поэтому каждому человеку пригодится она, поэтому учить её и понимать нужно уже со школьного возраста. Ведь не существует профессий, в которых не применялись бы математические знания, приобретенные в школе.
Математика позволяет человеку думать. В скором времени и мне необходимо будет определиться с будущей профессией, поэтому я считаю, что данная тема актуальна, а знание областей применения математики в последствие дает мне стимул к учению.
Слайд 5Историческая справка.
Яков Исидорович Перельман – российский, советский учёный, популяризатор физики, математики
Яков Исидорорович Перельман
Слайд 6Создание нового жанра уже само по себе – выдающееся литературное явление,
Слайд 7История возникновения науки «математика»
Слово "математика" происходит от греческого слова "матейн" (mathein)
Слайд 8Оптические иллюзии.
Оптических иллюзий существует очень много. Приведу несколько простых примеров, представляющих
- иллюзии, вызванные особым расположением линий и фигур Отрезок, расположенный вертикально, кажется длиннее, чем такой же отрезок, расположенный горизонтально. Квадрат, заштрихованный горизонтальными линиями, кажется более широким, чем равный ему квадрат, заштрихованный вертикальными.
иллюзии, вызванные контрастами
Круг, расположенный в центре в окружении шести больших кругов, кажется меньше такого же круга, но окруженного шестью маленькими кругами. Вот как обманчиво воздействие контраста окружения.
Слайд 9- иллюзии, возникшие в результате отвлечения внимания
Глядя на рисунок, мы понимаем,
Слайд 10
иллюзии, вызванные нарушением ритма. Пример с кругами, на которые можно
- иллюзии, возникающие в результате контраста чёрное – белое. Белый крест на чёрном фоне кажется больше, чем чёрный крест на белом фоне.
Слайд 11Гексафлексагоны.
Никто не станет отрицать, что флексагоны – игрушки весьма занимательные, но
Слайд 12Это произошло в конце 1939 года. Как-то раз Артур Х. Стоун,
Взяв этот шестиугольник за два cмежных треугольника, Стоун подогнул противоположный угол так, что его вершина совпала с центром фигуры При этом Стоун обратил внимание на то, что, когда шестиугольник раскрывался словно бутон, видимой становилась совсем другая поверхность. Если бы обе стороны исходного шестиугольника были разного цвета, то после перегибания видимая поверхность изменила бы свою окраску. Так был открыт самый первый флексагон с тремя поверхностями.
Слайд 13Софизмы и парадоксы.
И.П. Натансон так определил парадокс и софизм: парадокс
Математическим софизмом принято называть не менее удивительные утверждения, в доказательствах которых в отличие от доказательства парадоксов кроются незаметные, а подчас и довольно тонкие ошибки.
Софизм-доказательство ложного утверждения, причем ошибка в доказательстве искусно замаскирована. Софистами называли группу древнегреческих философов IV-V вв. до н.э., достигших большого искусства в логике. В любой области математики свои софизмы. В лучших из них раccуждениях с тщательно замаскированной ошибкой позволяют приходить к самым невероятным заключениям.
Слайд 14Примеры софизмов.
Алгебраический софизм
Примером более тонкого математического софизма служит
Умножив обе его части на а —b, получим
a2—ab = ab + ас — Ь2— bс. Перенесем ас в левую часть:
а2 — ab — ас = ab — b2 — bс разложим на множители:
а (а — Ь —с) = b(a—b — с). Разделив обе части равенства на a — b — с, найдем a = b, что и требовалось доказать.
Ещё один пример софизма. Если равны половины, то равны и целые. Полуполное есть то же, что и полупустое, значит, полное-то же самое, что пустое.
Арифметический софизм 1=2
Никто не станет возражать, что 3-1=6-4. если обе части этого очевидного равенства умножим на (-1), то получим 1-3=4-6. К обеим частям равенства можно прибавить одинаковые числа:1-3+9/4=4-6+9/4. Обе части представляют собой квадраты разностей выражений (1-3/2)2= (2-3/2)2. Из обеих частей извлекаем квадратный корень:1-3/2=2-3/2. К обеим частям прибавим 3/2; имеем на это полное право. Тогда получим 1=2. Аналогично можно доказать, что 2=3.
Слайд 15Пример парадокса.
Как-то раз хозяину одной великолепной гостиницы с бесконечным, но счетным
Слайд 16Невозможные фигуры.
В 1954 году Роджер и Лайонел Пенроузы опубликовали в Британском
Слайд 17
В этой статье невозможный треугольник был представлен в его классическом виде
Слайд 18Интересные задачи на логику и не только.
С помощью циркуля и
Решение. Ясно, что задача сводится к построению угла в 1°, далее все просто. Заметим, что 19 х 19 = 361, то есть сумма девятнадцати углов в 19° есть окружность плюс 1°. Сложение углов при помощи циркуля и линейки является стандартной, хорошо решаемой задачей. Получив угол в 1°, далее отложим этот угол девятнадцать раз и получим угол в 19°.
Слайд 20 В стозначном числе 12345678901234567890…1234567890 вычеркнули все цифры, стоящие на нечетных
Решение:
Сначала будут вычеркнуты все нечетные числа. Останется 10 групп четных цифр 2 4 6 8 0. После того как будет вычеркнуто еще 25 цифр, не вычеркнутые цифры образуют 5 групп по пять цифр 4 8 2 6 0. После очередного вычеркивания останется 12 цифр 8 6 4 2 0 8 6 4 2 0 8 6. После вычеркивания шести цифр останется 6 цифр 6 2 8 4 0 6, потом — 2 4 6, а затем цифра 4.
Ответ: 4
Слайд 21 Каким образом можно принести из реки шесть литров воды, если
Решение :
Сначала надо взять большое ведро (9 л) и налить туда воды. Взять маленькое ведро (4 л) и налить из большого ведра в маленькое. В большом осталось 5 л. Из маленького выливаем всю воду. Из большого ведра наливаем в маленькое воду. В большом ведре остался 1 л. Выливаем из маленького ведра всю воду. Переливаем из большого в маленькой 1 л. Наливаем в большое ведро воду. Переливаем из большого в маленькое ведро воду. В большом ведре осталось 6 л. Таблица: Ведро 9 л | 9 | 5 | 5 | 1 | 1 | 0 | 9 | 6 | Ведро 4 л | 0 | 4 | 0 | 4 | 0 | 1 | 1 | 4 |
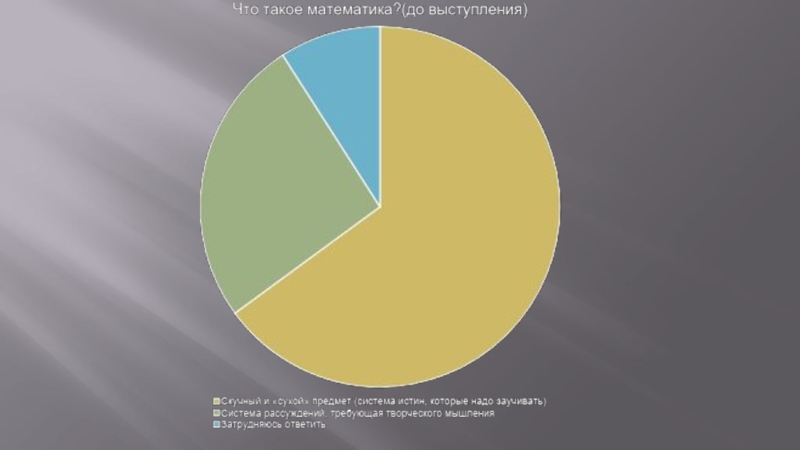
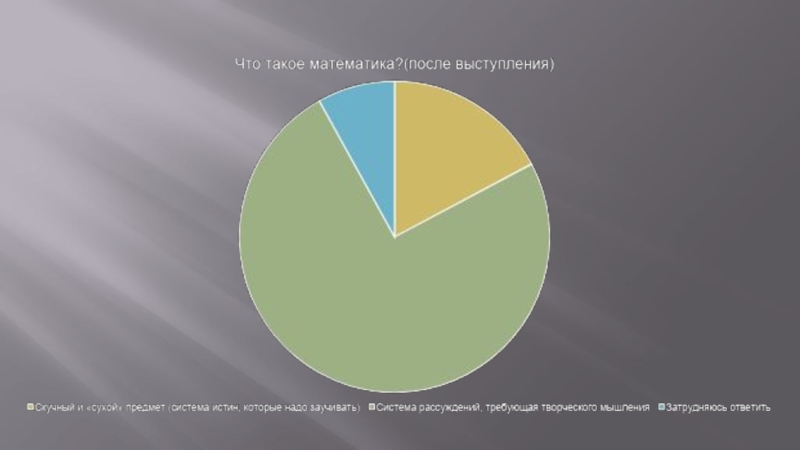
Слайд 22Социологический опрос.
Я решил провести опрос сверстников с целью выяснения их отношения
Слайд 25Вывод
Выполняя эту исследовательскую работу, я проанализировал и переработал очень много математической
Если раньше я не мог убедить, что математика – не скучный и «сухой» предмет, то на этот раз мне удалось это сделать. Это можно увидеть из результата социологического опроса. В нашей жизни много математики, а может быть и одна сплошная математика! Как и в жизни в ней много странного, невероятного и загадочного!
Я показал и убедил, что математику надо рассматривать не как систему истин, которые надо заучивать, а как систему рассуждений, требующую творческого мышления.