Презентация, доклад на тему Задачи с параметрами на логарифмы

5 ≤ а ≤ 12

Пусть сos 2 x + 1= t; t ϵ [1; 2];

тогда уравнение примет вид

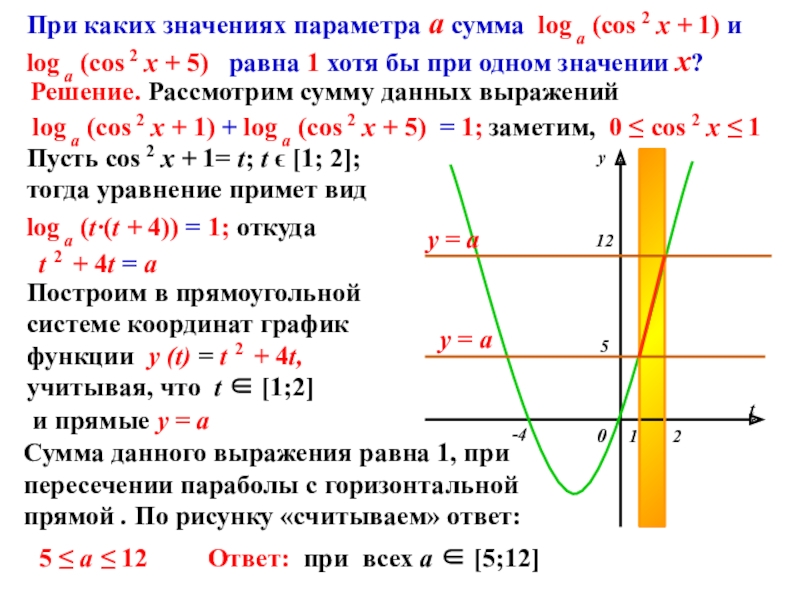
При каких значениях параметра а сумма log a (cos 2 x + 1) и log a (cos 2 x + 5) равна 1 хотя бы при одном значении х?

log a (cos 2 x + 1) + log a (cos 2 x + 5) = 1;

заметим, 0 ≤ cos 2 x ≤ 1

log a (t∙(t + 4)) = 1; откуда

t 2 + 4t = a

у = а

у = а

Ответ: при всех a  [5;12]

х

у

2

-2

3

3

1

5

А

В

С

О

Найдите все значения параметра а, при которых количество
корней уравнения (5 - а) х 3 – 4 х 2 + х = 0 равно количеству
общих точек линий х 2 + у 2 = а 2 и у = 5 - │х - 1│

Заметим, что х = 0 – корень не зависимо от параметра а. Уравнение (5 - а) х 2 – 4 х + 1 = 0 может иметь 0, 1 или 2 решения в зависимости от параметра а и D = 4(a – 1).

а = 5; а = 1