Матвей.
- Главная
- Разное
- Образование
- Спорт
- Естествознание
- Природоведение
- Религиоведение
- Французский язык
- Черчение
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, фоны, картинки для презентаций
- Экология
- Экономика
Презентация, доклад на тему Задачи по алгебре 9 класс
Содержание
- 1. Задачи по алгебре 9 класс
- 2. Задача. Смешали 30%-й раствор соляной
- 3. Решение 1. Обозначим x массу первого раствора,
- 4. Решение 2. Приравнивание площадей равновеликих прямоугольников: 15x
- 5. Задача. Имеется лом стали двух сортов с
- 6. Решение.С использованием графика: (приравнивание площадей равновеликих прямоугольников)10*х
- 7. Задача. Сплавили два слитка серебра: 75
- 8. Решение.Пусть проба сплава равна х. Составим диагональную схему:Получаем:
- 9. Задача. От двух кусков сплава
- 10. Решение. Обозначим массу отрезанного
- 11. Задача. Из сосуда, доверху
- 12. Решение.Пусть сосуд вмещает х литров, тогда в сосуде после отливания 2-х литров осталось (х-2) литра91х-182+110=79х91х-79х=7212х=72х=6
- 13. Задача. Имеются два слитка
- 14. Решение.360+40=400 (г) масса 1 куска(360/400)*100% = 90(%)
- 15. Задача. Имеется два сплава,
- 16. Решение. Пусть
- 17. Спасибо за внимание!
Задача. Смешали 30%-й раствор соляной кислоты с 10%-ым раствором и получили 600 г 15%-го раствора. Сколько граммов каждого раствора надо было взять?
Слайд 1Задачи по алгебре:
сплавы и растворы
Презентацию выполнили:
ученики 9 Б класса
Пилипенко Никита,
Янголенко
Слайд 2Задача. Смешали 30%-й раствор соляной кислоты с 10%-ым раствором и получили 600
г 15%-го раствора. Сколько граммов каждого раствора надо было взять?
Слайд 3Решение 1.
Обозначим x массу первого раствора, тогда масса второго (600
- x).
Составим уравнение:
30x + 10* (600 - x) = 600 *15
x = 150
Составим уравнение:
30x + 10* (600 - x) = 600 *15
x = 150
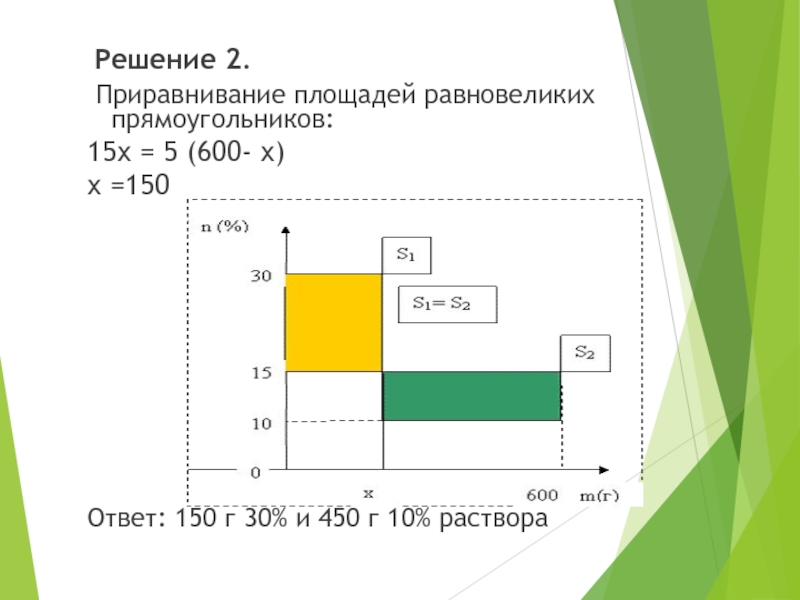
Слайд 4 Решение 2.
Приравнивание площадей равновеликих прямоугольников:
15x = 5 (600- x)
x
=150
Ответ: 150 г 30% и 450 г 10% раствора
Ответ: 150 г 30% и 450 г 10% раствора
Слайд 5Задача. Имеется лом стали двух сортов с содержанием никеля 5% и 40%.
Сколько нужно взять металла каждого из этих сортов, чтобы получить140 т стали с содержанием 30% никеля?
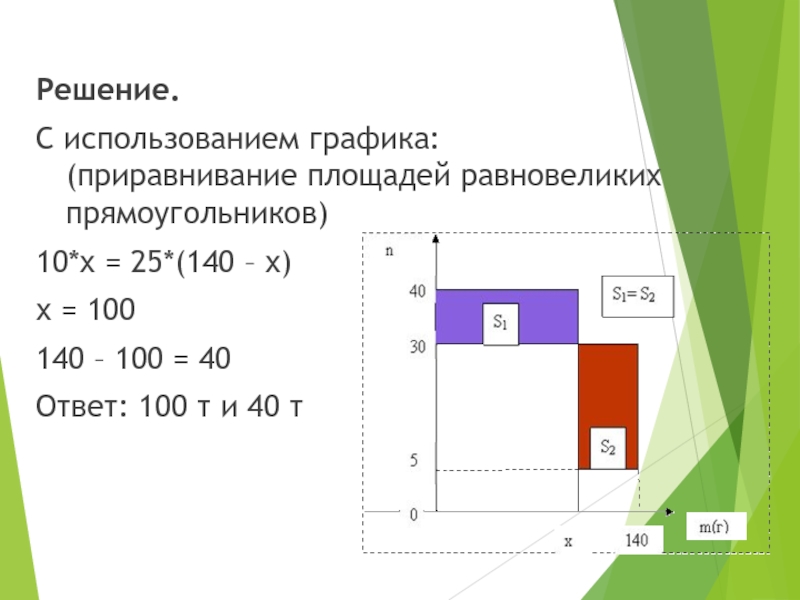
Слайд 6Решение.
С использованием графика:
(приравнивание площадей равновеликих прямоугольников)
10*х = 25*(140 – х)
х =
100
140 – 100 = 40
Ответ: 100 т и 40 т
140 – 100 = 40
Ответ: 100 т и 40 т
Слайд 7Задача.
Сплавили два слитка серебра: 75 г 600-й и 150
г 864-й пробы. Определить пробу сплава.
Слайд 8Решение.
Пусть проба сплава равна х. Составим диагональную схему:
Получаем: (864 – х): (х – 600)
= 75: 150
1728 – 2х = х – 600
х = 776.
Ответ: сплав 776-й пробы.
1728 – 2х = х – 600
х = 776.
Ответ: сплав 776-й пробы.
Слайд 9Задача.
От двух кусков сплава с массами 3 кг
и 2 кг и с концентрацией меди 0,6 и 0,8 отрезали по куску равной массы. Каждый из отрезанных кусков сплавлен с остатком другого куска, после чего концентрация меди в обоих сплавах стала одинаковой. Какова масса каждого из отрезанных кусков?
Слайд 10 Решение.
Обозначим массу отрезанного куска х (кг). Так
как в обоих сплавах концентрация меди после двух операция стала одинаковой, то массы сплавов и массы меди в этих сплавах пропорциональны. Первоначально массы меди в сплавах равны 0,6*3(кг) и 0,8*2(кг). После того, как отрезали куски массой х(кг), содержание меди стало 0,6(3-х) и 0,8(2-х), а после сплавления 0,6(3-х) + 0,8х и 0,8(2-х) +0,6х
х = 1,2
Ответ: 1,2 кг
х = 1,2
Ответ: 1,2 кг
Слайд 11 Задача.
Из сосуда, доверху наполненного 91%-м раствором кислоты,
отлили 2 литра 55%-го раствора этой же кислоты. После этого в сосуде получился 79%-й раствор кислоты. Сколько литров вмещает сосуд?
Слайд 12Решение.
Пусть сосуд вмещает х литров, тогда в сосуде после отливания 2-х
литров осталось (х-2) литра
91х-182+110=79х
91х-79х=72
12х=72
х=6
91х-182+110=79х
91х-79х=72
12х=72
х=6
Слайд 13 Задача.
Имеются два слитка сплава серебра и олова.
Первый слиток содержит 360 г серебра и 40 г олова. От каждого слитка взяли по куску, сплавили их и получили 200 г сплава, в котором оказалось 81% серебра. Определите массу куска, взятого от второго слитка.
Слайд 14Решение.
360+40=400 (г) масса 1 куска
(360/400)*100% = 90(%) концентрация серебра в 1
куске
450+150=600(г) масса 2 куска
(450/600)*100%=75(%) концентрация серебра во 2-м куске
Пусть нужно взять х г от второго куска, тогда от первого взяли (200-х) г. По расчетной формуле:
18000-90х+75х=16200
-15х = -1800
х=120
Ответ: 120г.
450+150=600(г) масса 2 куска
(450/600)*100%=75(%) концентрация серебра во 2-м куске
Пусть нужно взять х г от второго куска, тогда от первого взяли (200-х) г. По расчетной формуле:
18000-90х+75х=16200
-15х = -1800
х=120
Ответ: 120г.
Слайд 15 Задача.
Имеется два сплава, состоящие из цинка, меди
и олова. Известно, что первый сплав содержит 40% олова, а второй – 26% меди. Процентное содержание цинка в первом и во втором сплавах одинаково. Сплавив 150 кг первого сплава и 250 кг второго, получили новый сплав, в котором оказалось 30% цинка. Определите, сколько килограммов олова содержится в получившемся новом сплаве.
Слайд 16 Решение.
Пусть х кг – количество
олова в новом сплаве. Так как новый сплав весит 400 кг и в нём находится 30 % цинка, то он содержит 400*30/100=120 кг, а во втором сплаве (120-y) кг цинка. По условию задачи процентное содержание цинка в двух сплавах равно, следовательно, можно составить уравнение: 100y/150=100(120-y)/250
Из этого уравнения находим, что у=45. Поскольку первый сплав содержит 40% олова, то в 150 кг первого сплава олова будет 150*40/100=60 кг, а во втором сплаве олова будет (х-60) кг. Поскольку второй сплав содержит 26% меди, то во втором сплаве меди будет 250*26/100=65 кг. Во втором сплаве олова содержится (х-60) кг, цинка 120-45=75 (кг), меди 65 кг и, так как весь сплав весит 250 кг, то имеем:
х-60+75+65=250, откуда х=170 кг
Ответ: 170 кг.
Из этого уравнения находим, что у=45. Поскольку первый сплав содержит 40% олова, то в 150 кг первого сплава олова будет 150*40/100=60 кг, а во втором сплаве олова будет (х-60) кг. Поскольку второй сплав содержит 26% меди, то во втором сплаве меди будет 250*26/100=65 кг. Во втором сплаве олова содержится (х-60) кг, цинка 120-45=75 (кг), меди 65 кг и, так как весь сплав весит 250 кг, то имеем:
х-60+75+65=250, откуда х=170 кг
Ответ: 170 кг.