Выполнила учитель математики
МБОУ «Гимназия № 1 имени К.И.Щёлкина»
Пояркова Ирина Викторовна
- Главная
- Разное
- Образование
- Спорт
- Естествознание
- Природоведение
- Религиоведение
- Французский язык
- Черчение
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, фоны, картинки для презентаций
- Экология
- Экономика
Презентация, доклад на тему Взаимное расположение сферы и плоскости
Содержание
- 1. Взаимное расположение сферы и плоскости
- 2. «Знание – самое превосходное из владений.
- 3. Проверка домашнего заданияВариант 11. О(2;-3;0), R=5.2. (x-2)²
- 4. Определение сферы.Сферой называется поверхность, состоящая из всех
- 5. Определение шара.Тело, ограниченное сферой, называется шаром.Центр, радиус
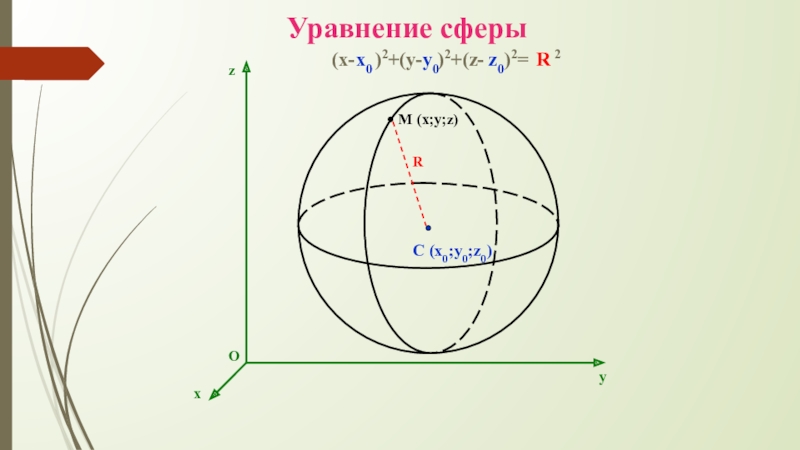
- 6. Уравнение сферыR(x- )2+(y- )2+(z- )2= 2
- 7. Постановка проблемыРассмотрим задачу № 586 на стр.
- 8. Тема урока: Взаимное расположение сферы и плоскостиЦели:изучить
- 9. Взаимное расположение окружности и прямойrdЕсли d <
- 10. Взаимное расположение сферы и плоскости Введем прямоугольную
- 11. Слайд 11
- 12. 1 случайЕсли расстояние от центра сферы до
- 13. Если же секущая плоскость не проходит через
- 14. 2 случайЕсли расстояние от центра сферы до
- 15. Свойство касательной плоскости к сфереРадиус сферы, проведенный
- 16. 3 случайЕсли расстояние от центра сферы до
- 17. ЗАРЯДКА ДЛЯ ГЛАЗ
- 18. Слайд 18
- 19. № 586. Отрезок ОН-высота тетраэдра ОАВС. Выясните
- 20. Решение: чтобы выяснить взаимное расположение сферы и плоскости,
- 21. Самостоятельная работа с самопроверкой ВАРИАНТ 11.
- 22. № 580Решениеd < R, значит, сечением
- 23. O№ 581 Вершины треугольника АВС лежат
- 24. № 592 Радиус сферы равен 112
- 25. Итог урокаНа этом уроке мы рассмотрели
- 26. Слайд 26
Слайд 1 Взаимное расположение сферы и плоскости.
Слайд 2«Знание – самое превосходное из владений. Все стремятся к нему, само
Ал - Бируни
Слайд 3Проверка домашнего задания
Вариант 1
1. О(2;-3;0), R=5.
2. (x-2)² + y² + (z+1)²
3. Да.
4. О(-1;1;0), R=2.
Вариант 2
1. О(-3;0;1), R=4.
2. (x+2)² + (y-1)² + z² = 36.
3. Да.
4. О(1;0;-1), R=2.
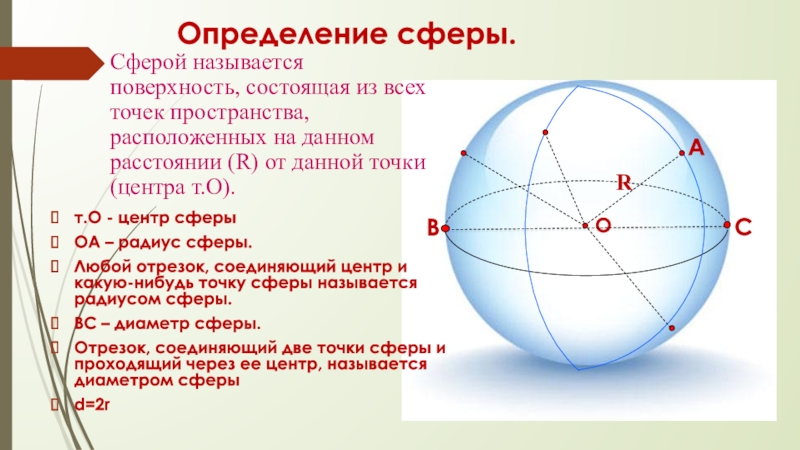
Слайд 4Определение сферы.
Сферой называется поверхность, состоящая из всех точек пространства, расположенных на
O
А
R
B
C
т.О - центр сферы
ОА – радиус сферы.
Любой отрезок, соединяющий центр и какую-нибудь точку сферы называется радиусом сферы.
ВС – диаметр сферы.
Отрезок, соединяющий две точки сферы и проходящий через ее центр, называется диаметром сферы
d=2r
Слайд 5Определение шара.
Тело, ограниченное сферой, называется шаром.
Центр, радиус и диаметр сферы являются
Шар радиуса R и центром О содержит все точки пространства, которые расположены от т. О на расстоянии, не превышающем R.
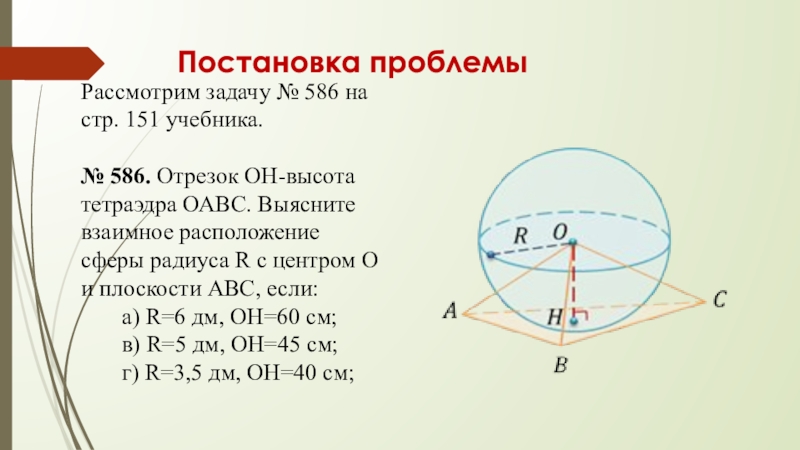
Слайд 7Постановка проблемы
Рассмотрим задачу № 586 на стр. 151 учебника.
№ 586. Отрезок
а) R=6 дм, ОН=60 см;
в) R=5 дм, ОН=45 см;
г) R=3,5 дм, ОН=40 см;
Слайд 8Тема урока: Взаимное расположение сферы и плоскости
Цели:
изучить виды взаимного расположения сферы
сформировать навыки решения задач.
Задача: провести исследование взаимного расположения сферы и плоскости в зависимости от соотношения между радиусом сферы и расстоянием от ее центра до плоскости.
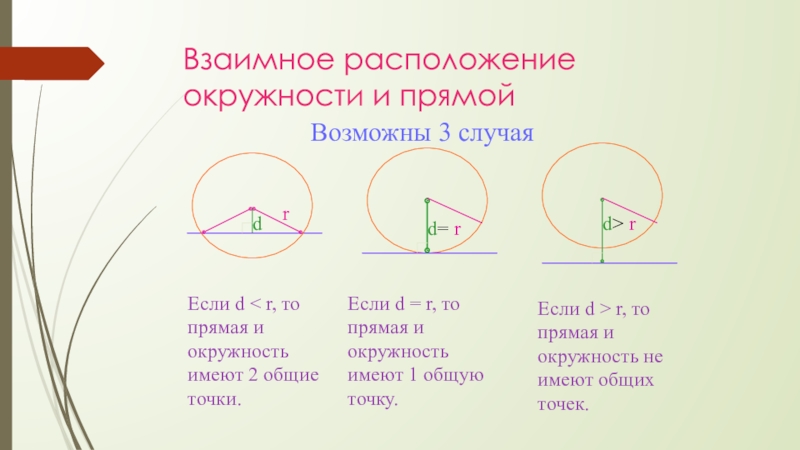
Слайд 9Взаимное расположение окружности и прямой
r
d
Если d < r, то прямая и
d= r
d> r
Если d = r, то прямая и окружность имеют 1 общую точку.
Если d > r, то прямая и окружность не имеют общих точек.
Возможны 3 случая
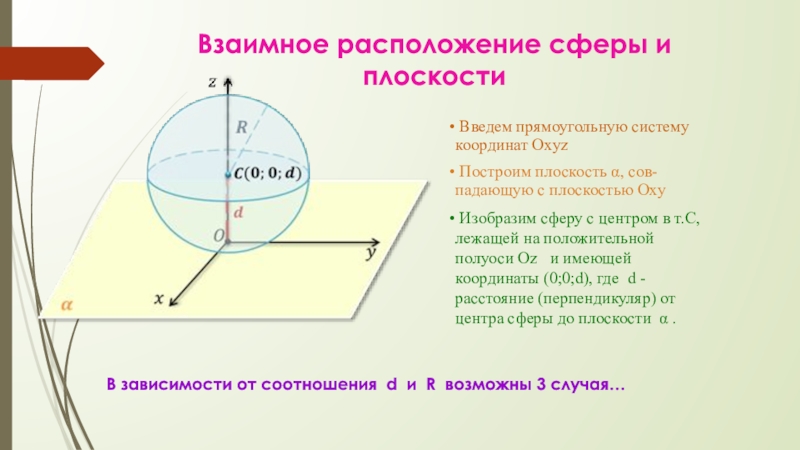
Слайд 10Взаимное расположение сферы и плоскости
Введем прямоугольную систему координат Oxyz
Построим
Изобразим сферу с центром в т.С, лежащей на положительной полуоси Oz и имеющей координаты (0;0;d), где d - расстояние (перпендикуляр) от центра сферы до плоскости α .
В зависимости от соотношения d и R возможны 3 случая…
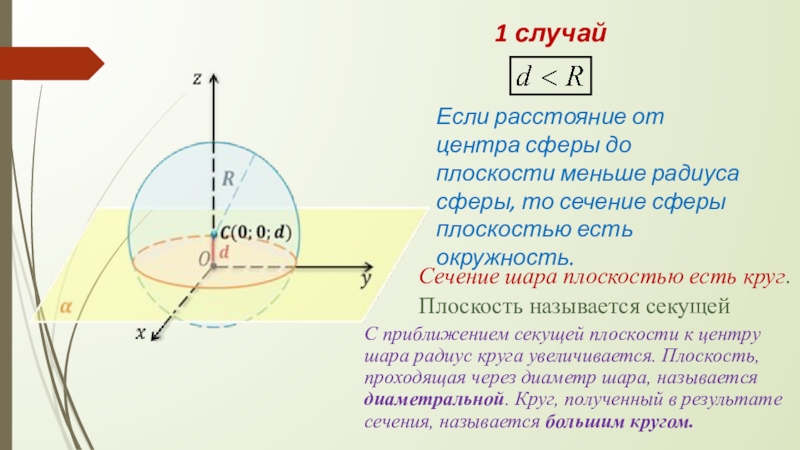
Слайд 121 случай
Если расстояние от центра сферы до плоскости меньше радиуса сферы,
Сечение шара плоскостью есть круг.
Плоскость называется секущей
С приближением секущей плоскости к центру шара радиус круга увеличивается. Плоскость, проходящая через диаметр шара, называется диаметральной. Круг, полученный в результате сечения, называется большим кругом.
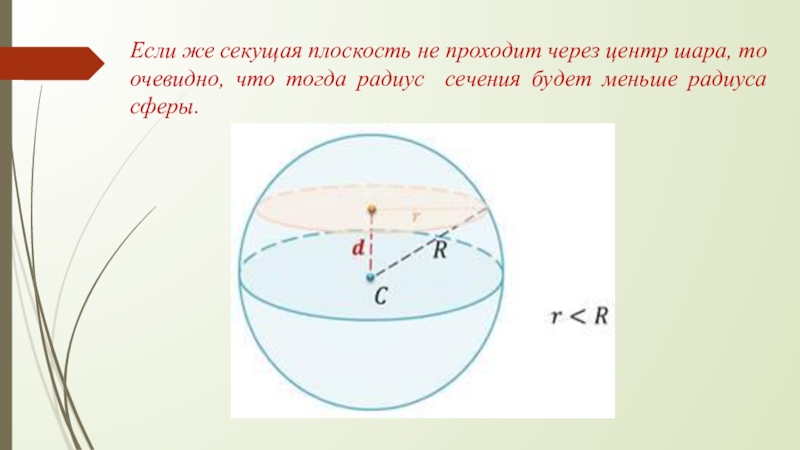
Слайд 13Если же секущая плоскость не проходит через центр шара, то очевидно,
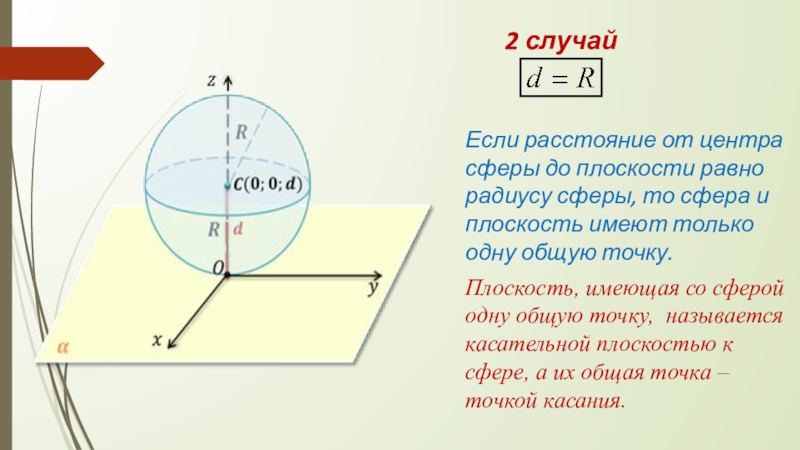
Слайд 142 случай
Если расстояние от центра сферы до плоскости равно радиусу сферы,
Плоскость, имеющая со сферой одну общую точку, называется касательной плоскостью к сфере, а их общая точка – точкой касания.
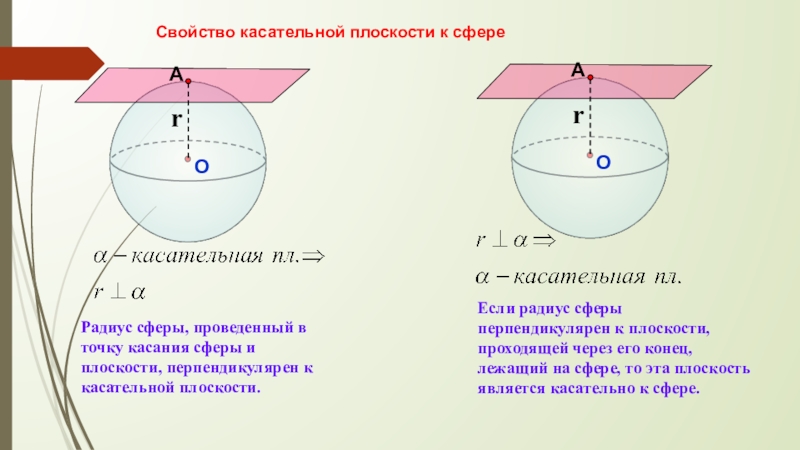
Слайд 15Свойство касательной плоскости к сфере
Радиус сферы, проведенный в точку касания сферы
Если радиус сферы перпендикулярен к плоскости, проходящей через его конец, лежащий на сфере, то эта плоскость является касательно к сфере.
Слайд 163 случай
Если расстояние от центра сферы до плоскости больше радиуса сферы,
Слайд 19
№ 586. Отрезок ОН-высота тетраэдра ОАВС. Выясните взаимное расположение сферы радиуса
а) R=6 дм, ОН=60 см;
в) R=5 дм, ОН=45 см;
г) R=3,5 дм, ОН=40 см;
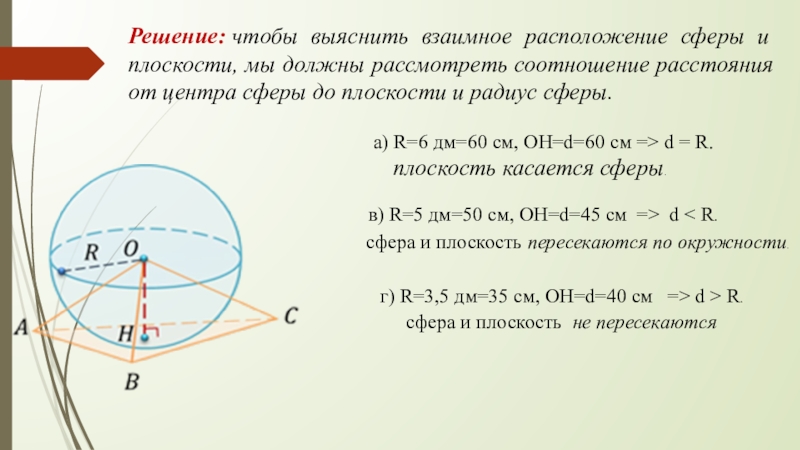
Слайд 20Решение: чтобы выяснить взаимное расположение сферы и плоскости, мы должны рассмотреть соотношение
а) R=6 дм=60 см, ОН=d=60 см => d = R.
плоскость касается сферы.
в) R=5 дм=50 см, ОН=d=45 см => d < R.
г) R=3,5 дм=35 см, ОН=d=40 см => d > R.
сфера и плоскость пересекаются по окружности.
сфера и плоскость не пересекаются
Слайд 21Самостоятельная работа с самопроверкой
ВАРИАНТ 1
1. Имеют только одну общую точку
2.
3. Не имеют общих точек
4.Больше 8 см
5. 13 см
6. От 1см до 3 см
ВАРИАНТ 2
1. Пересекаются по окружности
2. Имеют только одну общую точку
3. Не имеют общих точек
4. Больше 21 см
5. От 1см до 4 см
6. 7 см
Слайд 22№ 580
Решение
d < R, значит, сечением шара плоскостью является круг.
Дано: шар(О; R), R=41 дм, d=9дм
Найти: Sсеч.
Слайд 23O
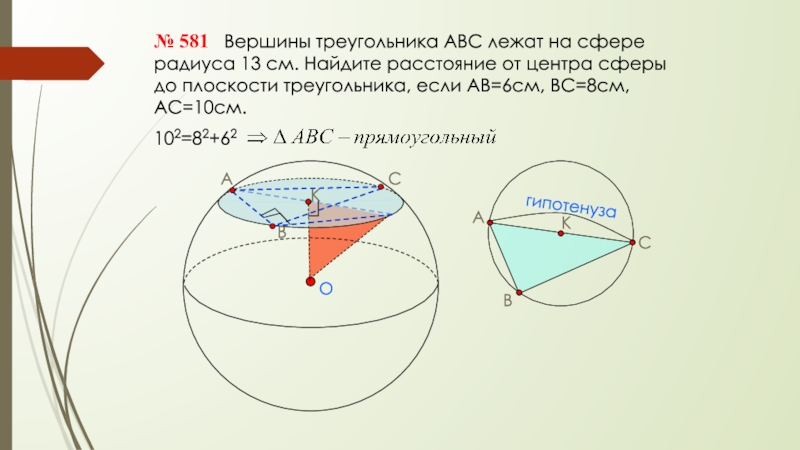
№ 581 Вершины треугольника АВС лежат на сфере радиуса 13
102=82+62
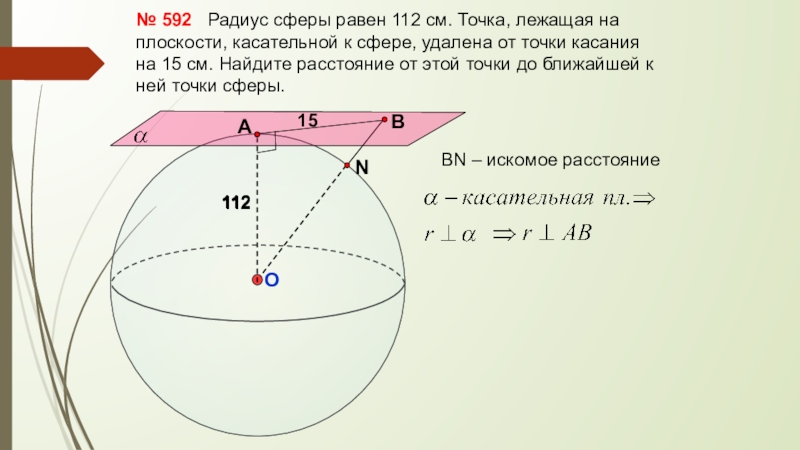
Слайд 24№ 592 Радиус сферы равен 112 см. Точка, лежащая на
А
112
О
ВN – искомое расстояние