- Главная
- Разное
- Образование
- Спорт
- Естествознание
- Природоведение
- Религиоведение
- Французский язык
- Черчение
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, фоны, картинки для презентаций
- Экология
- Экономика
Презентация, доклад на тему Виртуальный музей по математики Шаги к экзамену
Содержание
- 1. Виртуальный музей по математики Шаги к экзамену
- 2. ммМУЗЕЙ МАТЕМАТИКИДобро пожаловать в музей математики!
- 3. Наверх ВыйтиЗал числа.Зал близнецов и тройняшекЗал палиндромов
- 4. сВниз Первый шаг к экзаменуВыйтиЗал лучшей находкиВторой шаг к экзамену
- 5. Проверь себяНазадНайди ошибку
- 6. НазадОтвет
- 7. НазадОшибка заключается в том, что время должно
- 8. Проверь себяНазад
- 9. НазадРешениеРешу ЕГЭ №501542 Имеется два сосуда. Первый
- 10. Назад
- 11. НазадРешениеРешу ЕГЭ №99578 Имеются два сосуда. Первый
- 12. Назад
- 13. НазадРешениеРешу ЕГЭ №99575Смешав 30-процентный и 60-процентный растворы
- 14. Назад
- 15. НазадРешениеРешу ЕГЭ №99575Имеется два сплава. Первый содержит
- 16. Назад
- 17. НазадРешениеРешу ЕГЭ №99573Смешали 4 литра 15–процентного водного
- 18. Назад
- 19. НазадРешениеРешу ЕГЭ №99572Смешали некоторое количество 15–процентного раствора
- 20. Назад
- 21. Решу ЕГЭ №99571НазадВ сосуд, содержащий 5 литров
- 22. Назад
- 23. Решу ОГЭ №323750ПодсказкаВ – число целочисленных точеквнутри
- 24. Проверь себяНайди ошибкуЗадания для самостоятельной работыНазад
- 25. Леонтий Филиппович Магницкий (1669 — 1739) —
- 26. НазадПроверь себя
- 27. Назад
- 28. Решу ЕГЭ №249411ПодсказкаВ – число целочисленных точеквнутри
- 29. Назад
- 30. Решу ЕГЭ №27554ПодсказкаВ – число целочисленных точеквнутри
- 31. Назад
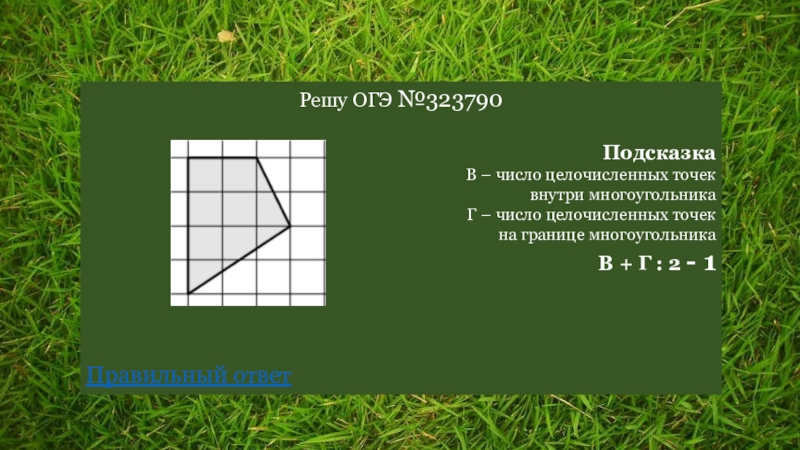
- 32. Решу ОГЭ №323790ПодсказкаВ – число целочисленных точеквнутри
- 33. Назад
- 34. Решу ЕГЭ №248891Найдите ошибкуПодсказкаВ – число целочисленных
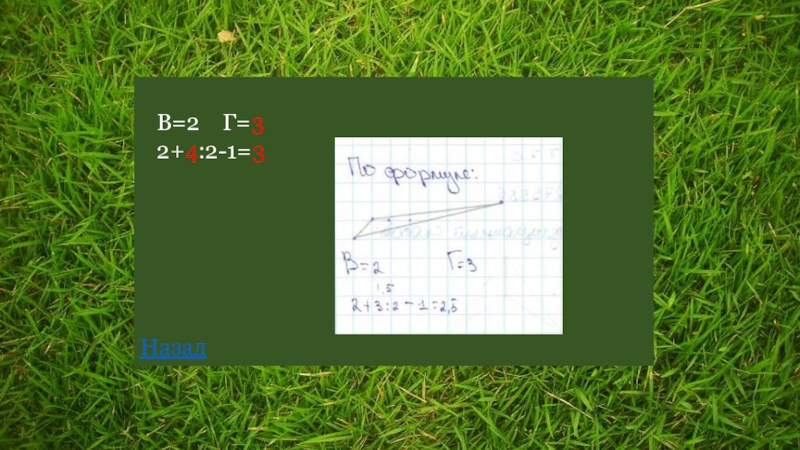
- 35. В=2 Г=3 2+4:2-1=3Назад
- 36. Решу ОГЭ №252617Найдите ошибкуПодсказкаВ – число целочисленных
- 37. В=23 Г=4 23+4:2-1=24Назад
- 38. Решу ОГЭ №323768 Найдите ошибкуПравильный ответ
- 39. 32+(22:2)+(35:2)=6+2+7,5=15,5Назад
- 40. Только в 30-х гг. ХХ века теория
- 41. Трагична судьба австрийского математика Георга Александра Пика
- 42. Решетка на плоскости является средством, которое позволяет
- 43. «То общее, чем пользуется любое искусство, а
- 44. Существует большое количество определений термина "число". О
- 45. В толковом словаре С.И. Ожегова определение числаЧИСЛО́,
- 46. НазадЗал числа
- 47. НазадЗал близнецов и тройняшек
- 48. Числовой палиндром — это натуральное число, которое
- 49. 31111311331131 31 13 313313 131назад
- 50. НазадНазадЗал палиндромов
- 51. В нашей школе учатся 4 пары близнецов:
- 52. НазадЛучшие находки
- 53. Посетив пять магазинов, я решила найти ответ
- 54. Ни для кого не секрет, что некоторые
- 55. Спасибо за внимание!
Слайд 1Виртуальный
«Музей удивительных чисел»
Выполнила: Андреева Елизавета, Руководитель: Кириллова Татьяна Николаевна, учитель математики.
Слайд 7Назад
Ошибка заключается в том, что время должно быть записано «1 мин
Слайд 9Назад
Решение
Решу ЕГЭ №501542
Имеется два сосуда. Первый содержит 100 кг, а
Слайд 11Назад
Решение
Решу ЕГЭ №99578
Имеются два сосуда. Первый содержит 30 кг, а
Слайд 13Назад
Решение
Решу ЕГЭ №99575
Смешав 30-процентный и 60-процентный растворы кислоты и добавив 10
Слайд 15Назад
Решение
Решу ЕГЭ №99575
Имеется два сплава. Первый содержит 10% никеля, второй —
Слайд 17Назад
Решение
Решу ЕГЭ №99573
Смешали 4 литра 15–процентного водного раствора некоторого вещества с
Слайд 19Назад
Решение
Решу ЕГЭ №99572
Смешали некоторое количество 15–процентного раствора некоторого вещества с таким
Слайд 21Решу ЕГЭ №99571
Назад
В сосуд, содержащий 5 литров 12–процентного водного раствора некоторого
Решение
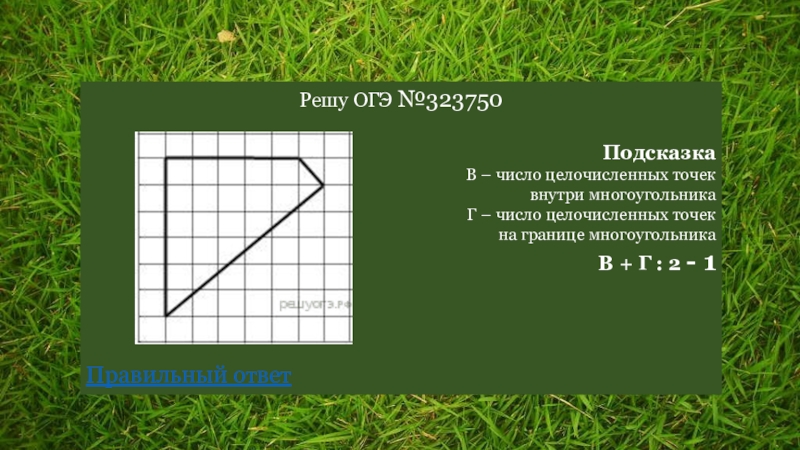
Слайд 23Решу ОГЭ №323750
Подсказка
В – число целочисленных точек
внутри многоугольника
Г – число целочисленных
на границе многоугольника
В + Г : 2 - 1
Правильный ответ
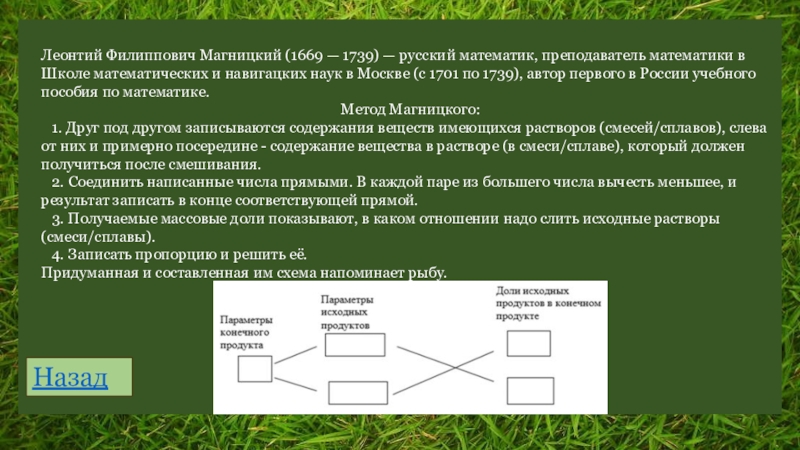
Слайд 25Леонтий Филиппович Магницкий (1669 — 1739) — русский математик, преподаватель математики
Метод Магницкого:
1. Друг под другом записываются содержания веществ имеющихся растворов (смесей/сплавов), слева от них и примерно посередине - содержание вещества в растворе (в смеси/сплаве), который должен получиться после смешивания.
2. Соединить написанные числа прямыми. В каждой паре из большего числа вычесть меньшее, и результат записать в конце соответствующей прямой.
3. Получаемые массовые доли показывают, в каком отношении надо слить исходные растворы (смеси/сплавы).
4. Записать пропорцию и решить её.
Придуманная и составленная им схема напоминает рыбу.
Назад
Слайд 28Решу ЕГЭ №249411
Подсказка
В – число целочисленных точек
внутри многоугольника
Г – число целочисленных
на границе многоугольника
В + Г : 2 - 1
Правильный ответ
Слайд 30Решу ЕГЭ №27554
Подсказка
В – число целочисленных точек
внутри многоугольника
Г – число целочисленных
на границе многоугольника
В + Г : 2 - 1
Правильный ответ
Слайд 32Решу ОГЭ №323790
Подсказка
В – число целочисленных точек
внутри многоугольника
Г – число целочисленных
на границе многоугольника
В + Г : 2 - 1
Правильный ответ
Слайд 34Решу ЕГЭ №248891
Найдите ошибку
Подсказка
В – число целочисленных точек
внутри многоугольника
Г – число
на границе многоугольника
В + Г : 2 - 1
Правильный ответ
Слайд 36Решу ОГЭ №252617
Найдите ошибку
Подсказка
В – число целочисленных точек
внутри многоугольника
Г – число
на границе многоугольника
В + Г : 2 - 1
Правильный ответ
Слайд 40 Только в 30-х гг. ХХ века теория решеток получила продолжение в
назад
Слайд 41 Трагична судьба австрийского математика Георга Александра Пика (10 августа 1859 —
У термина «формула Пика» существует и другое значение – «теорема Пика».
Формула Пика (или теорема Пика) — классический результат комбинаторной геометрии и геометрии чисел.
Площадь многоугольника с целочисленными вершинами вычисляется по формуле В + Г/2 -1, где В ⁻⁻ количество целочисленных точек внутри многоугольника, а
Г — количество целочисленных точек на границе многоугольника.
В частности площадь треугольника с вершинами в узлах и не содержащего узлов ни внутри, ни на сторонах (кроме вершин) равна ½.
назад
Слайд 42 Решетка на плоскости является средством, которое позволяет задачи алгебры, анализа, теории
Первую попытку сделал Дж. Буль в первой половине XIX века. Она привела к понятию булевой алгебры. В конце XIX века Ч. Пирс и Э. Шредер ввели понятие решетки. Их работа не привлекла внимание математической общественности, однако решетка стала для К. Гаусса стартовой точкой для сравнения площади круга с числом точек с целыми координатами, находящимися внутри него. Затем Г. Минковский создал геометрию чисел.
назад
Слайд 43«То общее, чем пользуется любое искусство, а также рассудок и знания,
назад
Слайд 44Существует большое количество определений термина "число". О числах первый начал рассуждать
так как 10 = 1 + 2 + 3 + 4. Оно считалось священным числом и олицетворяло всю Вселенную.
назад
Слайд 45В толковом словаре С.И. Ожегова определение числа
ЧИСЛО́, -а, мн. числа, -сел, -слам, ср.
1. Понятие количества,
А в толковом словаре русского языка под редакцией Д.В. Дмитриева мне встретились следующие определения: 1.Числом называется единичный элемент математических данных.2. Чётное число – это число, которое кратно 2(делится на 2). 3. Круглые числа – это такие числа, как 10,20 и другие, которые в записи в записи оканчиваются цифрой 0.
назад
Слайд 48Числовой палиндром — это натуральное число, которое читается слева направо, и
В книге «Есть идея!» Мартина Гарднера упоминается «гипотеза о палиндромах». Возьмём любое натуральное число и сложим его с числом, записанным теми же цифрами, но в обратном порядке. Проделаем то же действие с получившейся суммой и будем повторять его до тех пор, пока не получим палиндром. Суть гипотезы в том, что, взяв любое число, после конечного числа действий мы обязательно получим палиндром.
Пример: 13+31=44, 63+36=99, 65+56=121 (двузначные числа); 312+213=525(трёхзначные числа) и пришла к выводу, что не всегда достаточно сделать один шаг, чтобы получить в сумме число перевёртыш, чаще требуется не менее двух. Пример: число 97 порождает палиндром 44044 после выполнения шестого шага.
97+79 = 176; 176 + 671 = 847; 847 + 748 = 1595; 1595 + 5951= 7546;
7546 + 6457 = 14003; 14003 + 30041=44044.
назад
Слайд 51В нашей школе учатся 4 пары близнецов: братья Кочкуркины, Марк и
НАЗАД
Слайд 53Посетив пять магазинов, я решила найти ответ на вопрос: « Верны
Посетив ещё один известный магазин в нашем районе, узнаем: порошок стоил 163,50, на него скидка 38%, новая цена 99,90. Проверяем: 163,50:100=1,635 1,635x38=62,13 163,50-62,13=101,37. Магазин сделал скидку больше, чем указал. 163,50-99,90=63,60 63,60:1,635=38,8% Скидка больше на 0,8%.
Кондиционер стоил 132,50, со скидкой 24% цена стала 99,90. Проверяем: 132,50:100=1,325 1,325x24=31,80 132,50-31,80=100,70. Вновь скидку сделали больше. Узнаем, на сколько: 132,50-99,90=32,60 32,60:1,325=24,6%. Скидка больше на 0,6%.
Ещё один пример: масло оливковое стоило 429 рублей. Цену снизили до 279 рублей. Указана скидка 35%. Проверяем: 429:100=4,29 2,29x35=150,15 429-150,15=278,85 279 – 278,85 = 15 копеек. Магазин новую цену округлил с избытком.
Мы посетили четыре магазина, в трёх из них цены указаны неверно.
назад
Слайд 54Ни для кого не секрет, что некоторые автомобилисты стремятся заполучить для
Результаты меня удивили. 100% водителей дали отрицательный ответ на первый вопрос, а на второй вопрос мы услышали: «А что это за числа?». В нашей школе есть 5 учителей, которые водят автомобиль, но и среди них никто не дал правильный ответ. А вот три учителя английского языка справились с заданием.
назад