- Главная
- Разное
- Образование
- Спорт
- Естествознание
- Природоведение
- Религиоведение
- Французский язык
- Черчение
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, фоны, картинки для презентаций
- Экология
- Экономика
Презентация, доклад на тему Урок-презентация Решение дробно-рациональных уравнений (8 класс)
Содержание
- 1. Урок-презентация Решение дробно-рациональных уравнений (8 класс)
- 2. № 606Из города в село, находящееся от
- 3. Так как разница во времени двух автомобилей
- 4. Первый корень не удовлетворяет условиям задачи. Значит
- 5. №608Первый лыжник прошел расстояние в 20 км
- 6. Составь уравнение (учти, что разница во времени
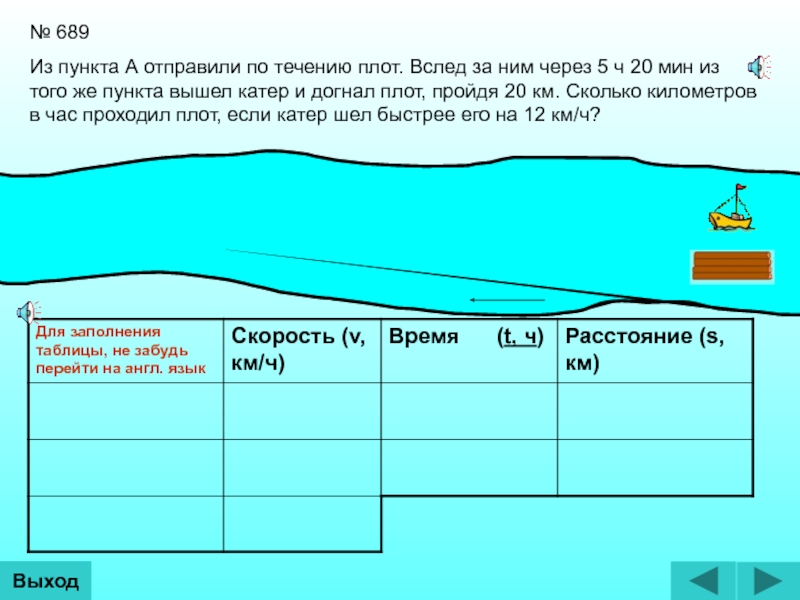
- 7. № 689Из пункта А отправили по течению
- 8. Теперь составь по условию уравнение и реши
- 9. №616Две бригады, работая совместно, закончили ремонт дома
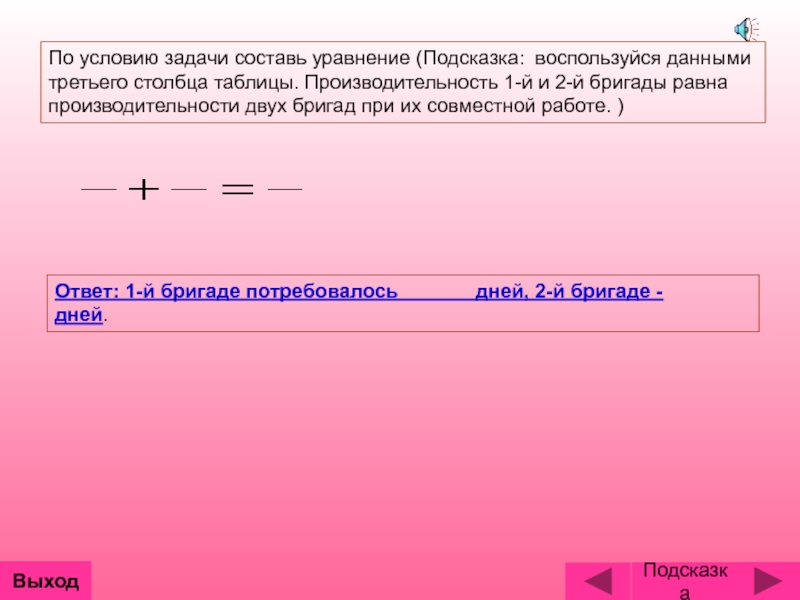
- 10. По условию задачи составь уравнение (Подсказка: воспользуйся
- 11. Наступило время поработать самостоятельно. Выбери уровень сложности:Уровень АУровень БУровень ВВыход
- 12. Уровень АЗадача №1
- 13. Уровень БЗадача №1Из пункта А в пункт
- 14. Уровень ВЗадача №1Лыжник должен был проехать 10
- 15. Задача № 608УравнениеРешение уравненияОтветА лучше вернись назад и попробуй решить сам! У тебя получится!!!
- 16. Уравнение к задаче №608Попробуй решить уравнение самостоятельно!
- 17. Решение уравнения к задаче №608(Умножим обе части
- 18. Ответ к задаче №608x2 = -12 не
- 19. Задача № 689УравнениеРешение уравненияОтветА лучше вернись назад и попробуй решить сам! У тебя получится !!!
- 20. Решение уравнения к задаче №689Попробуй решить уравнение самостоятельно!
- 21. Решение уравнения к задаче №689(Умножим обе части
- 22. Ответ к задаче №689x2 = -15 не удовлетворяет условию задачи. Следовательно скорость плота 3 км/ч.
- 23. Задача № 616ТаблицаУравнениеРешение уравненияОтвет
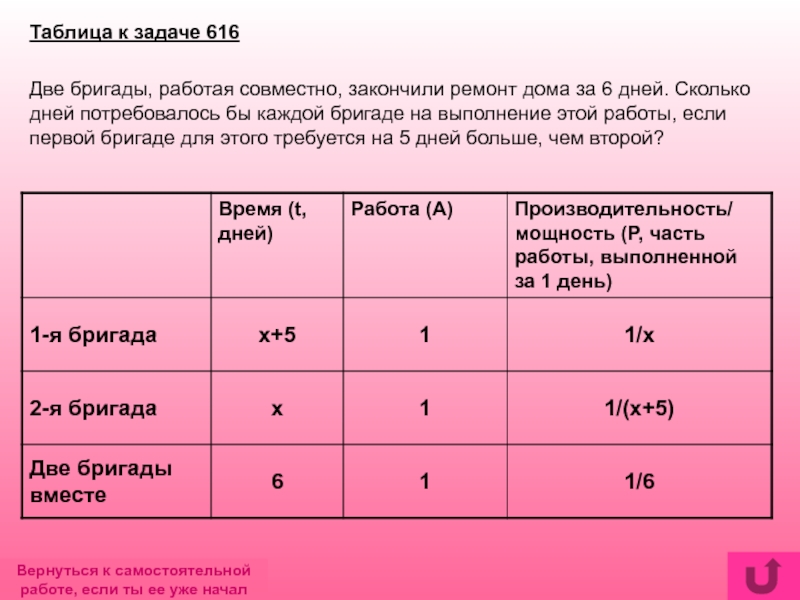
- 24. Таблица к задаче 616Две бригады, работая совместно,
- 25. Уравнение к задаче 616Попробуй решить уравнение самостоятельно!
- 26. Решение уравнения к задаче 616(Умножим обе части уравнения на общий знаменатель трех дробей: 3x(x+2))(Сократим дроби)(Упростим)2 корня,
- 27. Ответ к задаче 616x2 = -3 не
Слайд 2№ 606
Из города в село, находящееся от него на расстоянии 120
120 км
x+20 км/ч
x км/ч
Выход
(Чтобы заполнить таблицу, щелкай мышкой на пустых ячейках).
Слайд 3Так как разница во времени двух автомобилей равна 1 часу получим
Решаем уравнение. Умножим обе части уравнения на общий знаменатель x(x+20):
Выход
Слайд 4Первый корень не удовлетворяет условиям задачи. Значит скорость второго автомобиля равна
Ответ: 40 км/ч и 60 км/ч
Следующую задачу попробуем решить вместе!
Выход
Слайд 5
№608
Первый лыжник прошел расстояние в 20 км на 20 минут быстрее,
20 км
Выход
(Заполни таблицу самостоятельно, вводя данные в ячейки таблицы с клавиатуры.)
Слайд 6Составь уравнение (учти, что разница во времени – 20 мин =1/3
Ответ: Скорость первого лыжника км/ч , скорость второго - км/ч.
Реши уравнение самостоятельно и введи ответ вместо « ?».
Подсказка
Выход
Слайд 7
№ 689
Из пункта А отправили по течению плот. Вслед за ним
Выход
Слайд 8Теперь составь по условию уравнение и реши его! Введи ответ в
Ответ: скорость плота км/ч.
Если все получилось, то жми ! Еще одна задачка!
Если что-то не так, исправь ошибки и введи новый ответ.
Ну, а если совсем не получается, то можешь воспользоваться подсказкой.
Подсказка
Выход
(В крайнем случае можешь воспользоваться подсказкой).
Слайд 9
№616
Две бригады, работая совместно, закончили ремонт дома за 6 дней. Сколько
Подсказка
Выход
Слайд 10
По условию задачи составь уравнение (Подсказка: воспользуйся данными третьего столбца таблицы.
Ответ: 1-й бригаде потребовалось дней, 2-й бригаде - дней.
Подсказка
Выход
Слайд 11Наступило время поработать самостоятельно. Выбери уровень сложности:
Уровень А
Уровень Б
Уровень В
Выход
Слайд 12Уровень А
Задача №1
Из города А в город В, расстояние между которыми 120 км, выехали одновременно два велосипедиста. Скорость первого на 3 км/ч больше скорости второго, поэтому он прибыл в город В на 2 ч раньше. Определите скорости велосипедистов.
Задача №2
На двух копировальных машинах, работающих одновременно, можно сделать копию пакета документов за 10 мин. За какое время можно выполнить эту работу в отдельности на каждой машине, если известно, что при работе на первой машине для этого требуется на 15 мин больше, чем на второй. (Вспомни решение задачи )
Ответ: скорость 1-го - км/ч, 2-го - км/ч.
Ответ: на первой машине за мин., на второй за - мин.
Выход
№616
Слайд 13
Уровень Б
Задача №1
Из пункта А в пункт В, расстояние между которыми
Задача №2
Катер, собственная скорость которого 8 км/ч, прошел по реке расстояние 15 км по течению и такое же расстояние против течения. Найдите скорость течения реки, если время, затраченное на весь путь, равно 4 ч.
Задача №3
На двух копировальных машинах, работающих одновременно, сделали копию пакета документов за 20 мин. За какое время можно выполнить эту работу в отдельности на каждой машине, если известно, что при работа не первой машине для этого требуется на 30 мин меньше времени, чем на второй.
Ответ: скорость второго пешехода км/ч.
Ответ: скорость течения реки км/ч.
Ответ: на первой машине за мин., на второй за - мин.
Выход
Слайд 14Уровень В
Задача №1
Лыжник должен был проехать 10 км, чтобы в назначенное
Задача №2
Расстояние между двумя пристанями на реке равно 21 км. Моторная лодка отправилась от одной пристани к другой и через 4 часа вернулась обратно, затратив на стоянку 24 мин. Найдите собственную скорость лодки, если скорость течения равна 2 км/ч.
Задача №3
Первый завод может выполнить некоторый заказ на 4 дня быстрее, чем второй. За какое время может выполнить этот заказ каждый завод, если известно, что при совместной работе за 24 дня они выполнили заказ в пять раз больший.
Ответ: скорость лыжника - км/ч,
Ответ: собственная скорость лодки км/ч.
Ответ: 1-й завод выполнит заказ за дня, 2-й - за дня.
Выход
Слайд 15Задача № 608
Уравнение
Решение уравнения
Ответ
А лучше вернись назад и попробуй решить сам!
Слайд 17Решение уравнения к задаче №608
(Умножим обе части уравнения на общий знаменатель
(Сократим дроби)
(Упростим)
(Второй коэффициент четный. Найдем дискриминант по второй формуле)
2 корня,
Слайд 18Ответ к задаче №608
x2 = -12 не удовлетворяет условию задачи. Следовательно
Слайд 19Задача № 689
Уравнение
Решение уравнения
Ответ
А лучше вернись назад и попробуй решить сам!
Слайд 21Решение уравнения к задаче №689
(Умножим обе части уравнения на общий знаменатель
(Сократим дроби)
(Упростим)
2 корня,
(Поделим на 16),
Слайд 22Ответ к задаче №689
x2 = -15 не удовлетворяет условию задачи. Следовательно
Слайд 24Таблица к задаче 616
Две бригады, работая совместно, закончили ремонт дома за
Вернуться к самостоятельной
работе, если ты ее уже начал
Слайд 26Решение уравнения к задаче 616
(Умножим обе части уравнения на общий знаменатель
(Сократим дроби)
(Упростим)
2 корня,