- Главная
- Разное
- Образование
- Спорт
- Естествознание
- Природоведение
- Религиоведение
- Французский язык
- Черчение
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, фоны, картинки для презентаций
- Экология
- Экономика
Презентация, доклад на тему Урок обобщения и систематизации знаний по теме Решение неравенств
Содержание
- 1. Урок обобщения и систематизации знаний по теме Решение неравенств
- 2. Урок коррекции знанийЦель урока: Продолжить формирование знаний
- 3. Путь размышления - это путь самый благородный,Путь
- 4. Проверка домашнего задания
- 5. а. (-∞;5)б. [5;+∞)в. [-1;4]г. (5;+∞)Устные упражнениях
- 6. а. (0;4)б. [4;+∞)в. (0;4]г. (0;+∞)4х
- 7. а. 0,5б. 2в. -0,5г. 1При каких значениях х выражение не имеет смысл
- 8. а. 3б. 2в. -3г. Х - любоеПри каких значениях х выражение имеет смысл
- 9. а. 1б. -2в. -0,5г. -1При каких значениях х выражение не имеет смысл
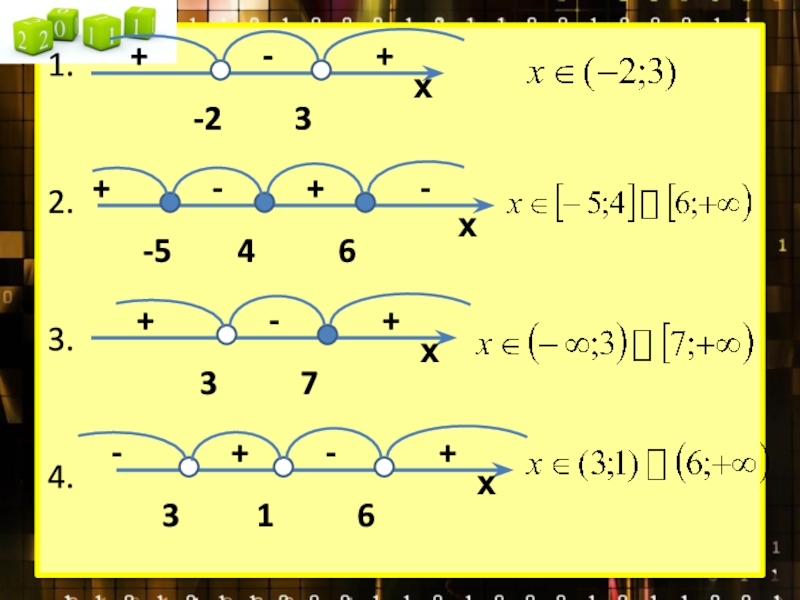
- 10. Находим нули функций.Отмечаем их на координатной прямой
- 11. Самостоятельная работа1 вариант2 вариант
- 12. 1. 2.3.4.
- 13. Работа у доски задание из КИМа 2014г.
- 14. эстафета
- 15. Исторические сюжеты на тему символики неравенствПоявление символики неравенств
- 16. Понятия «больше» и «меньше» наряду с понятием
- 17. Ряд неравенств приводит в своем знаменитом трактате
- 18. Современные знаки неравенств появились лишь в XVII—
- 19. Томас ГарриотНеравенства и системы неравенств широко используются
- 20. Символы нестрогого сравнения предложил Валлис в 1670
- 21. Эти обозначения были введены Анри Пуанкаре и Эмилем Борелем (1901) и
- 22. Самостоятельная работа. 1 вариантСтраница76Задание 1,2,3. 2 вариантСтраница77Задание 1,2,3.
- 23. Домашняя работа$1. Примеры 6,7,8 учебника.№1.20, 1.21.
- 24. сегодня я узнал… теперь я могу… я научился… было интересно…меня удивило… я приобрел… мне захотелось…Закончите фразу
- 25. «Красоту математики можно увидеть глазами, можно почувствовать
Слайд 1Амачкина А.А.
Учитель математики МБОУ « Средняя общеобразовательная школа №12 с углубленным
Слайд 2Урок коррекции знаний
Цель урока: Продолжить формирование знаний и умений решения неравенств
Решение рациональных
неравенств
Слайд 3Путь размышления - это путь самый благородный,
Путь подражания – самый легкий,
Путь опыта – самый горький.
/Конфуций/
Три пути ведут к знанию :
Слайд 10Находим нули функций.
Отмечаем их на координатной прямой
Определяем знаки функций в
Записываем ответ.
Напомните алгоритм решения
неравенства методом интервалов?
Слайд 16Понятия «больше» и «меньше» наряду с понятием равенства возникли в связи
Слайд 17Ряд неравенств приводит в своем знаменитом трактате «Начала» Евклид. Он, например,
Слайд 18Современные знаки неравенств
появились лишь в XVII— XVIII вв.
Знаки
математик Т. Гарриот (1560—1621)
Слайд 19Томас Гарриот
Неравенства и системы неравенств широко используются как в теоретических исследованиях,
Слайд 20Символы нестрогого сравнения предложил Валлис в 1670 году. Первоначально черта была
Джон Ва́ллис,
Пьер Бугер
Слайд 21Эти обозначения были введены Анри Пуанкаре
и Эмилем Борелем
(1901) и использовались для указания, что
Анри Пуанкаре
Эмилем Борелем
Слайд 24сегодня я узнал…
теперь я могу…
я научился…
было интересно…
меня удивило…
я приобрел…
мне захотелось…
Закончите фразу
Слайд 25«Красоту математики можно увидеть глазами, можно почувствовать сердцем, но объять её
Советский, грузинский и российский педагог и психолог
Шалва Александрович Амонашвили




![Урок обобщения и систематизации знаний по теме Решение неравенств а. (-∞;5)б. [5;+∞)в. [-1;4]г. (5;+∞)Устные упражнениях а. (-∞;5)б. [5;+∞)в. [-1;4]г. (5;+∞)Устные упражнениях](/img/thumbs/d02b3c5d200afb26366fc1c80fa62791-800x.jpg)
![Урок обобщения и систематизации знаний по теме Решение неравенств а. (0;4)б. [4;+∞)в. (0;4]г. (0;+∞)4х а. (0;4)б. [4;+∞)в. (0;4]г. (0;+∞)4х](/img/thumbs/9245432c575620901da158da3a6249e3-800x.jpg)