- Главная
- Разное
- Образование
- Спорт
- Естествознание
- Природоведение
- Религиоведение
- Французский язык
- Черчение
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, фоны, картинки для презентаций
- Экология
- Экономика
Презентация, доклад на тему Тригонометрия в треугольнике
Содержание
- 1. Тригонометрия в треугольнике
- 2. Цели: 1. Познакомиться с понятиями синуса, косинуса,
- 3. Что нам известно о прямоугольном треугольнике? АВСАВ
- 4. Синус, косинус, тангенс острого угла прямоугольного треугольника
- 5. Значения синуса, косинуса и тангенса для углов
- 6. Значения синуса, косинуса и тангенса для угла
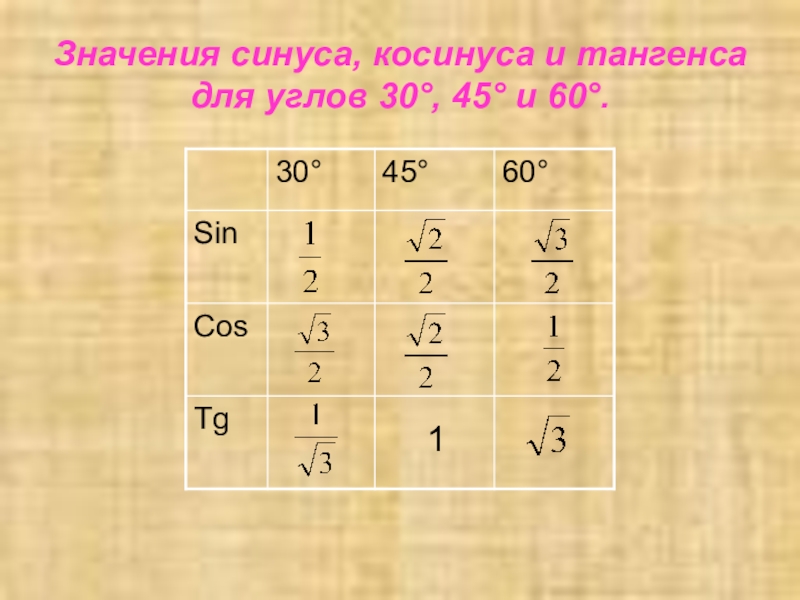
- 7. Значения синуса, косинуса и тангенса для углов 30°, 45° и 60°.1
- 8. Свойства синуса, косинуса и тангенса. tg
- 9. Контрольные вопросы: 1. Дайте определение синуса, косинуса
Слайд 2Цели:
1. Познакомиться с понятиями синуса, косинуса, тангенса острого угла прямоугольного
2. Рассмотреть свойства новых понятий, возможность их применения при решении задач.
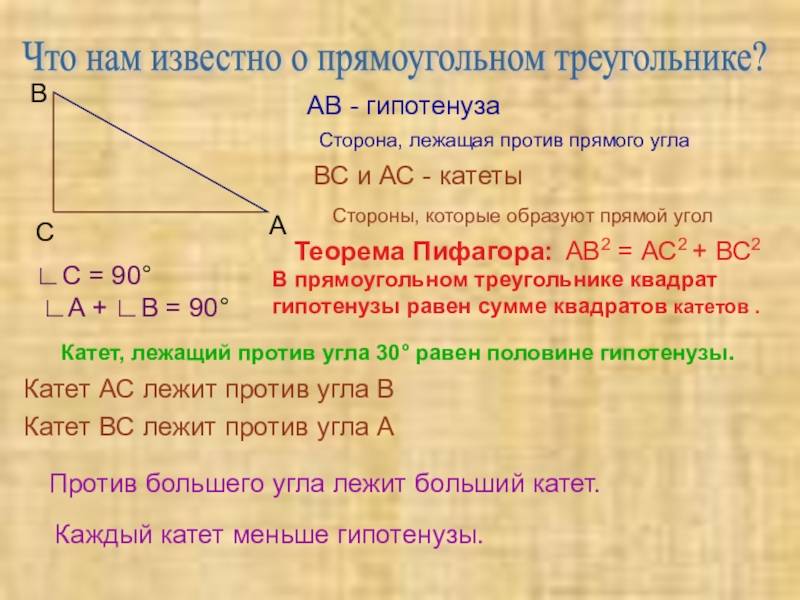
Слайд 3Что нам известно о прямоугольном треугольнике?
А
В
С
АВ - гипотенуза
Сторона, лежащая против
ВС и АС - катеты
Стороны, которые образуют прямой угол
∟A + ∟В = 90°
∟С = 90°
Катет ВС лежит против угла А
Катет АС лежит против угла В
Теорема Пифагора:
В прямоугольном треугольнике квадрат гипотенузы равен сумме квадратов катетов .
АВ2 = АС2 + ВС2
Катет, лежащий против угла 30° равен половине гипотенузы.
Против большего угла лежит больший катет.
Каждый катет меньше гипотенузы.
Слайд 4Синус, косинус, тангенс острого угла прямоугольного треугольника
с
а
в
Cos∟A =
Tg∟A =
Sin∟A =
A
B
C
Cинусом острого угла прямоугольного треугольника называется отношение противолежащего катета к гипотенузе.
Тангенсом острого угла прямоугольного треугольника называется отношение противолежащего катета к прилежащему катету.
Из длин сторон треугольника можно составить различные отношения:
= Sin∟В
= Cos∟В
Tg∟В =
Косинусом острого угла прямоугольного треугольника называется отношение прилежащего катета к гипотенузе.
Слайд 5Значения синуса, косинуса и тангенса для углов 30° и 60°.
с
а
в
B
60°
30°
90°
sin30°=
(а2+в2=с2).
соs 30°=
tg 30°=
sin 60°=
соs60°=
tg60°=
А
С
с = 2в;
а2 = с2- в2= 4в2 – в2 = 3в2;
а = в
=
=
=
=
=
=
Теорема Пифагора:
Слайд 6Значения синуса, косинуса и тангенса для угла 45° .
соs45°=
sin 45°=
tg45°=
А
В
С
а
с
а
45°
45°
90°
с2=а2 + а2 = 2а2;
с =
=
=
=
=
1
Слайд 8Свойства синуса, косинуса и тангенса.
tg a =
sin2a +
Основные тригонометрические тождества.
sin a
cоs a
Гипотенуза больше любого катета, поэтому…
Синус и косинус острого угла прямоугольного треугольника меньше единицы, но больше нуля.
Слайд 9Контрольные вопросы:
1. Дайте определение синуса, косинуса и тангенса
острого угла
2. Вспомните, каковы значения синуса, косинуса и тангенса углов 30°, 45°, 60°.
Домашнее задание: п. 66, 67, стр.156.
Вопросы 15,16,17,18 на стр. 161