Шудраков Николай Николаевич
- Главная
- Разное
- Образование
- Спорт
- Естествознание
- Природоведение
- Религиоведение
- Французский язык
- Черчение
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, фоны, картинки для презентаций
- Экология
- Экономика
Презентация, доклад на тему Теория вероятностей. Задачи повышенной сложности (Математика 11 класс)
Содержание
- 1. Теория вероятностей. Задачи повышенной сложности (Математика 11 класс)
- 2. Несовместные событияДва события А и В называются
- 3. Объединение событийПусть событие С означает, что произошло
- 4. Вероятность несовместных событийЕсли события А и В
- 5. Независимые событияДва события А и В называются
- 6. Пересечение событийПусть событие С означает, что произошло
- 7. Вероятность независимых событийЕсли события А и В
- 8. Частота событияЧастотой события А называют отношение m
- 9. Задачи об объединении несовместных событий1. На экзамене
- 10. Задачи об объединении несовместных событий2. Вероятность, что
- 11. Задачи об объединении несовместных событий3. Из районного
- 12. Задачи о пересечении независимых событий1. Если гроссмейстер
- 13. Задачи о пересечении независимых событий2. В магазине
- 14. Задачи о пересечении независимых событий3. В магазине
- 15. Задачи о пересечении независимых событий4. Биатлонист пять
- 16. Задачи о пересечении независимых событий5. Мышка заползает
- 17. Задачи об объединении пересечений событий1. Ковбой Билл
- 18. Задачи об объединении пересечений событий2. Автоматическая линия
- 19. Задачи об объединении пересечений событий3. Две фабрики
- 20. Задачи об объединении пересечений событий4. Чтобы пройти
Несовместные событияДва события А и В называются несовместными, если отсутствуют исходы, благоприятные одновременно как событию А, так и событию В.ПРИМЕР:Бросают кубик. События «выпало число 3» и «выпало четное число» несовместны.При этом события «выпало число больше 3»
Слайд 1Теория вероятностей.
Задачи повышенного и высокого уровней сложности
Математика 11 класс
МБОУ СШ №12
Учитель:
Слайд 2Несовместные события
Два события А и В называются несовместными, если отсутствуют исходы,
благоприятные одновременно как событию А, так и событию В.
ПРИМЕР:
Бросают кубик. События «выпало число 3» и «выпало четное число» несовместны.
При этом события «выпало число больше 3» и выпало четное число» совместны.
ПРИМЕР:
Бросают кубик. События «выпало число 3» и «выпало четное число» несовместны.
При этом события «выпало число больше 3» и выпало четное число» совместны.
Слайд 3Объединение событий
Пусть событие С означает, что произошло хотя бы одно из
событий А и В. Тогда событие С называют объединением (суммой) событий А и В.
С = А U В
С = А U В
Слайд 4Вероятность несовместных событий
Если события А и В несовместны, то вероятность их
объединения равна сумме вероятностей событий А и В.
Р(А U В) = Р(А) + Р(В)
Р(А U В) = Р(А) + Р(В)
Слайд 5Независимые события
Два события А и В называются независимыми, если вероятность каждого
из них не зависит от появления или непоявления другого события
ПРИМЕР:
Выполнили два подбрасывания монеты. События «при первом подбрасывании выпала решка» и «привтором подбрасывании выпал орел» независимы.
В урне 2 белых и 2 черных шара. Событие «первый извлеченный шар белый» и «второй извлеченный шар черный - зависимые.
ПРИМЕР:
Выполнили два подбрасывания монеты. События «при первом подбрасывании выпала решка» и «привтором подбрасывании выпал орел» независимы.
В урне 2 белых и 2 черных шара. Событие «первый извлеченный шар белый» и «второй извлеченный шар черный - зависимые.
Слайд 6Пересечение событий
Пусть событие С означает, что произошло как событие А, так
и В. Тогда событие С называют пересечением (произведением) событий А и В.
С = А ∩ В
С = А ∩ В
Слайд 7Вероятность независимых событий
Если события А и В независимы, то вероятность их
пересечения равна произведению вероятностей событий А и В.
Р(А ∩ В) = Р(А) ∙ Р(В)
Р(А ∩ В) = Р(А) ∙ Р(В)
Слайд 8Частота события
Частотой события А называют отношение m / n, где n
– общее число испытаний, m – число появления события А.
ПРИМЕР:
Мы подбросили монету 100 раз, орел выпал 47 раз. Частота выполнения орла равна 47/100=0,47
ПРИМЕР:
Мы подбросили монету 100 раз, орел выпал 47 раз. Частота выполнения орла равна 47/100=0,47
Слайд 9Задачи об объединении несовместных событий
1. На экзамене по геометрии школьнику достается
один вопрос из списка экзаменационных вопросов. Вероятность того, что это вопрос на тему «Ромб», равна 0,1. Вероятность того, что это вопрос на тему «Окружность», равна 0,15. Вопросов, относящихся одновременно к этим двум темам, нет.
Найдите вероятность того, что на экзамене школьнику достанется вопрос по одной из этих двух тем.
Найдите вероятность того, что на экзамене школьнику достанется вопрос по одной из этих двух тем.
Слайд 10Задачи об объединении несовместных событий
2. Вероятность, что новая кофемолка прослужит больше
года , равна 0,93.
Вероятность того, что она прослужит больше двух лет, равна 0,81. Найдите вероятность того, что кофемолка прослужит меньше двух лет, но больше года.
Вероятность того, что она прослужит больше двух лет, равна 0,81. Найдите вероятность того, что кофемолка прослужит меньше двух лет, но больше года.
Слайд 11Задачи об объединении несовместных событий
3. Из районного центра в деревню ежедневно
ходит автобус. Вероятность того, что в понедельник в автобусе окажется меньше 25 пассажиров, равна 0,91. Вероятность того, что окажется меньше 18 пассажиров, равна 0,39. Найдите вероятность того, что число пассажиров будет от 18 до 25.
Слайд 12Задачи о пересечении независимых событий
1. Если гроссмейстер К. играет белыми, то
он выигрывает у гроссмейстера Н. с вероятностью 0,45. Если К. играет черными, то он выигрывает с вероятностью 0,4. Гроссмейстеры К. и Н. играют две шахматные партии, причем во второй партии меняют цвет фигур.
Найдите вероятность того, что К. выиграет оба раза.
Найдите вероятность того, что К. выиграет оба раза.
Слайд 13Задачи о пересечении независимых событий
2. В магазине три продавца. Каждый из
них занят с клиентом с вероятностью 0,4. Найдите вероятность того, что в случайный момент времени все три продавца заняты (клиенты заходят независимо друг от друга).
Слайд 14Задачи о пересечении независимых событий
3. В магазине стоят два платежных автомата.
Каждый из них может быть неисправен с вероятностью 0,1 независимо от другого автомата. Найдите вероятность того, что хотя бы один автомат исправен.
Слайд 15Задачи о пересечении независимых событий
4. Биатлонист пять раз стреляет по мишеням.
Вероятность попадания в мишень при одном выстреле равна 0,6. Найдите вероятность того, что биатлонист первые два раза попал в мишени, а последние три – промахнулся. Результат округлите до сотых.
Слайд 16Задачи о пересечении независимых событий
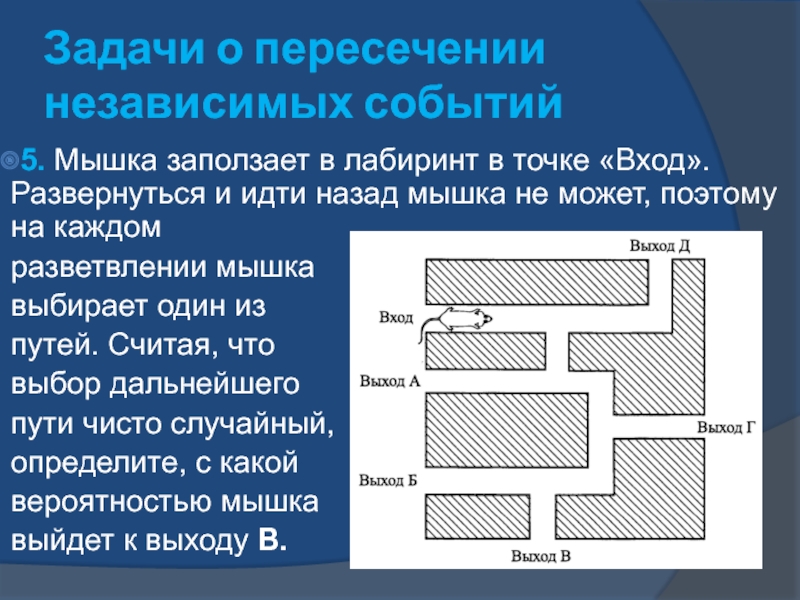
5. Мышка заползает в лабиринт в точке
«Вход». Развернуться и идти назад мышка не может, поэтому на каждом
разветвлении мышка
выбирает один из
путей. Считая, что
выбор дальнейшего
пути чисто случайный,
определите, с какой
вероятностью мышка
выйдет к выходу В.
разветвлении мышка
выбирает один из
путей. Считая, что
выбор дальнейшего
пути чисто случайный,
определите, с какой
вероятностью мышка
выйдет к выходу В.
Слайд 17Задачи об объединении пересечений событий
1. Ковбой Билл попадает в муху на
стене с вероятностью 0,8, если стреляет из пристрелянного револьвера. Если Билл стреляет из непристрелянного револьвера, то он попадает в муху с вероятностью 0,25. На столе лежат 5 револьверов, из них 2 пристрелянные. Ковбой Билл видит на стене муху, наудачу хватает первый попавшийся револьвер и стреляет в муху.
Найдите вероятность того, что Билл попадет в муху.
Найдите вероятность того, что Билл попадет в муху.
Слайд 18Задачи об объединении пересечений событий
2. Автоматическая линия изготавливает батарейки. Вероятность того,
что готовая батарейка неисправна, равна 0,05. Перед упаковкой каждая батарейка проходит систему контроля. Вероятность того, что система забракует неисправную батарейку, равна 0,98. Вероятность того, что система по ошибке забракует исправную батарейку, равна 0,08.
Найдите вероятность того, что случайно выбранная батарейка будет забракована системой контроля.
Найдите вероятность того, что случайно выбранная батарейка будет забракована системой контроля.
Слайд 19Задачи об объединении пересечений событий
3. Две фабрики выпускают одинаковые стекла для
автомобильных фар. Первая фабрика выпускает 60% этих стёкол, вторая 40%. Первая фабрика выпускает 4% бракованных стёкол, а вторая 3%.
Найдите вероятность того, что случайно купленное стекло окажется бракованным.
Найдите вероятность того, что случайно купленное стекло окажется бракованным.
Слайд 20Задачи об объединении пересечений событий
4. Чтобы пройти в следующий круг соревнований,
футбольной команде нужно набрать хотя бы 4 очка в двух играх. Если команда выигрывает, она получает 3 очка, в случае ничьей – 1 очко, если проигрывает – 0 очков. Найдите вероятность того, что команде удастся выйти в следующий круг соревнований. Считайте, что в каждой игре вероятность выигрыша и проигрыша одинаковы и равны 0,3.