- Главная
- Разное
- Образование
- Спорт
- Естествознание
- Природоведение
- Религиоведение
- Французский язык
- Черчение
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, фоны, картинки для презентаций
- Экология
- Экономика
Презентация, доклад на тему Тема урока: Комбинаторика. Комбинаторные конструкции
Содержание
- 1. Тема урока: Комбинаторика. Комбинаторные конструкции
- 2. КОМБИНАТОРИКА
- 3. 4=сТ4=цИИ
- 4. КОНСТРУКЦИИ
- 5. ТЕМА УРОКА:Комбинаторика. Комбинаторные конструкции
- 6. Цели: повторить основные понятия комбинаторики;отработка навыков решения комбинаторных задач с использованием формул перестановок, размещений, сочетаний.
- 7. Комбинаторика - это раздел математики, в котором
- 8. Задачи, в которых идёт речь о тех или иных комбинациях, называются -КОМБИНАТОРНЫМИ ЗАДАЧАМИ
- 9. Основные элементы комбинаторикиФакториал
- 10. Факториал.Факториал – это произведение всех натуральных чисел от 1 до n. Обозначение n!
- 11. Вопрос:Где встречаются комбинаторные задачи в реальной жизни?
- 12. Комбинаторные задачи в реальной жизни встречаются:лингвистика (рассмотрение
- 13. производство (распределение нескольких видов работ между рабочими);география (раскраска карт);спортивные соревнования (расчёт количества игр между участниками);
- 14. химия (анализ возможных связей между химическими элементами);агротехника (размещение посевов на нескольких полях);азартные игры (подсчёт частоты выигрышей);
- 15. астрология (анализ расположения планет и созвездий);биология (расшифровка кода ДНК);военное дело (расположение подразделений);
- 16. доставка почты (рассмотрение вариантов пересылки).экономика (анализ вариантов купли-продажи акций);криптография (разработка методов шифрования);
- 17. Основные элементы комбинаторики
- 18. ПерестановкиСочетанияРазмещения
- 19. Перестановки.
- 20. Задача №: 1Несколько стран в качестве символа
- 21. Отличительной особенностью перестановок является то, что
- 22. Сколькими способами можно рассадить 5 человек за столом?Р5=5!=1*2*3*4*5=120 способамиОтвет: 120 способамиЗадача №: 2
- 23. Устный счетВыбрать правильный ответ:
- 24. Вычислить:
- 25. Задача №3 Сколько существует анаграмм для слова КАТЕР ?Решение:P5 = 5!=5∙4∙3∙2∙1=120 Ответ: 120
- 26. «10 выпускников пришли в кафе отпраздновать окончание
- 27. Формула размещенияЧитается: «A из n по m»
- 28. Задача № 5Сколько трехзначных чисел можно составить
- 29. Слайд 29
- 30. Задача №7Студенты 1 курса изучают 10 предметов.
- 31. Формула сочетанияЧитается: «С из n по m»
- 32. Задача № 8Имеется 5 цветков разного цвета.
- 33. Задача №9В магазине «Филателия» продается 8 различных
- 34. Задача № 10Из 18-ти студентов группы надо
- 35. Комбинаторные конструкции
- 36. Ребусы ОтветыРебус №1.-«Комбинаторика»Ребус №2.-«Выборка»Ребус №3.-«События»Ребус №4.-«Достоверное»Ребус №5.-«Невозможное»Ребус №6.-«Случайные»Ребус №7.-«Совокупность»Ребус №8.-«Противоположные»Ребус №9.-«Равновозможное»Ребус №10.-«Совместное»
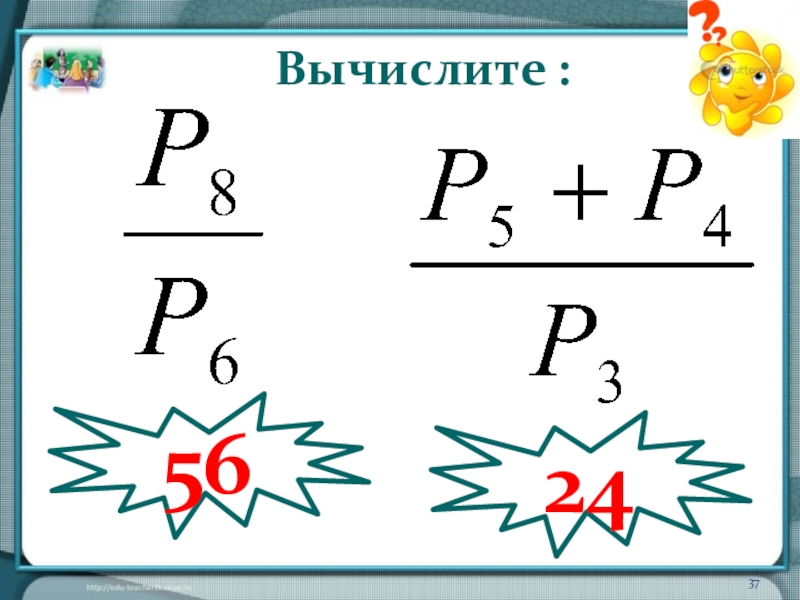
- 37. Вычислите :5624
- 38. № 1Из шести врачей поликлиники двух необходимо
- 39. Ответы:№ 1№ 2№ 3 №4
- 40. Ответы:№1 а) 2; б) 24;
- 41. Домашняя работаЗадания на карточках
- 42. Повторили: основные понятия комбинаторики; формулы для нахождения
- 43. Слайд 43
- 44. Выберите смайлик, который соответствует Вашему настроению в
КОМБИНАТОРИКА
Слайд 6Цели:
повторить основные понятия комбинаторики;
отработка навыков решения комбинаторных задач с
использованием формул перестановок, размещений, сочетаний.
Слайд 7
Комбинаторика - это раздел математики, в котором изучаются вопросы о том,
сколько различных комбинаций, подчиненных тем или иным условиям, можно составить из заданных объектов.
Слайд 12Комбинаторные задачи в реальной жизни встречаются:
лингвистика (рассмотрение вариантов комбинаций букв).
учебные заведения
(составление расписаний);
сфера общественного питания (составление меню);
Слайд 13производство (распределение нескольких видов работ между рабочими);
география (раскраска карт);
спортивные соревнования (расчёт
количества игр между участниками);
Слайд 14химия (анализ возможных связей между химическими элементами);
агротехника (размещение посевов на нескольких
полях);
азартные игры (подсчёт частоты выигрышей);
Слайд 15астрология (анализ расположения планет и созвездий);
биология (расшифровка кода ДНК);
военное дело (расположение
подразделений);
Слайд 16доставка почты (рассмотрение вариантов пересылки).
экономика (анализ вариантов купли-продажи акций);
криптография (разработка методов
шифрования);
Слайд 19Перестановки.
Перестановкой называется
множество, в котором установлен
порядок элементов.
порядок элементов.
Число перестановок из n элементов
вычисляется по формуле:
Pn = n!
Читается: «P из n» равно «n факториал»
По определению: 0! = 1 и 1! = 1
Слайд 20Задача №: 1
Несколько стран в качестве символа своего государства решили использовать
флаг в виде трех горизонтальных полос одинаковых по ширине, но разных по цвету: белый, синий, красный.
Сколько стран могут использовать такую символику при условии, что у каждой страны свой, отличный от других, флаг?
Сколько стран могут использовать такую символику при условии, что у каждой страны свой, отличный от других, флаг?
P3 = 3! = 1 ∙ 2 ∙ 3 = 6
Решение:
Ответ: 6
Слайд 21
Отличительной особенностью перестановок является то, что в каждой из них участвует
ВСЁ множество, то есть, все объекты. Например, дружная семья.
Слайд 22Сколькими способами можно рассадить 5 человек за столом?
Р5=5!=1*2*3*4*5=120 способами
Ответ: 120 способами
Задача
№: 2
Слайд 25Задача №3
Сколько существует анаграмм для слова КАТЕР ?
Решение:
P5 = 5!=5∙4∙3∙2∙1=120
Ответ: 120
Слайд 26«10 выпускников пришли в кафе отпраздновать окончание школы, но не могли
решить, как сесть, т.е. в каком порядке. На выручку пришёл официант, который предложил сесть сегодня, как придётся, а на другой день сесть по - другому и так до тех пор, пока не наступит такой день, когда они сядут как в первый раз. Тогда их официант обещал угостить бесплатным обедом. Как вы думаете, долго ли друзьям ждать бесплатного обеда?»
Задача №4
Решение:
10! = 3 628 800
Учитывая, что в году 365 дней, то это почти 9942 года.
Ответ: около 10 000 лет.
Слайд 28Задача № 5
Сколько трехзначных чисел можно составить из цифр 1, 3,
5 и 7, используя в записи числа каждую из них не более одного раза?
Решение:
Ответ: 24
Слайд 29
Задача №6
Сколько имеется слов длиной 3 с неповторяющимися буквами в алфавите из 6 букв ?
Решение:
Ответ: 120
Слайд 30Задача №7
Студенты 1 курса изучают 10 предметов. Сколькими способами можно составить
расписание на один день, чтобы в нем было 4 различных предмета?
Решение:
Ответ: 5040
Слайд 32Задача № 8
Имеется 5 цветков разного цвета. Обозначим их буквами a,
b, c, d, e. Требуется составить букет из трех цветков.
Решение:
Ответ: 10
Слайд 33Задача №9
В магазине «Филателия» продается 8 различных наборов марок, посвященных спортивной
тематике. Сколькими способами можно выбрать из них 3 набора?
Решение:
Ответ: 56
Слайд 34Задача № 10
Из 18-ти студентов группы надо выбрать двух дежурных. Сколькими
способами можно сделать этот выбор?
Решение:
Ответ: 153
Слайд 36Ребусы
Ответы
Ребус №1.-«Комбинаторика»
Ребус №2.-«Выборка»
Ребус №3.-«События»
Ребус №4.-«Достоверное»
Ребус №5.-«Невозможное»
Ребус №6.-«Случайные»
Ребус №7.-«Совокупность»
Ребус №8.-«Противоположные»
Ребус №9.-«Равновозможное»
Ребус
№10.-«Совместное»
Слайд 38№ 1
Из шести врачей поликлиники двух необходимо отправить на курсы повышения
квалификации. Сколькими способами это можно сделать?
№ 2
Сколько различных двухзначных чисел можно составить, используя цифры 1, 2, 3, 4 при условии, что ни одна цифра не повторяется?
№ 2
Сколько различных двухзначных чисел можно составить, используя цифры 1, 2, 3, 4 при условии, что ни одна цифра не повторяется?
№ 3
В группе 7 студентов успешно занимаются математикой. Сколькими способами можно выбрать из них двоих для участия в олимпиаде по предмету?
№ 4
Сколько различных трехзначных чисел можно составить из цифр 1, 2, 3, 4, 5 при условии, что ни одна цифра не повторяется?
Слайд 40Ответы:
№1
а) 2; б) 24; в) 720;
г) 40320
№2 а) 504; б) 42840; в) 1680; г) 30
№3 а) 20; б) 21; в) 561; г) 4845
№2 а) 504; б) 42840; в) 1680; г) 30
№3 а) 20; б) 21; в) 561; г) 4845
Слайд 42Повторили:
основные понятия комбинаторики; формулы для нахождения простейших комбинаций (перестановок, размещений
и сочетаний).
Научились:
вычислять количество перестановок, размещений и сочетаний;
решать простейшие комбинаторные задачи.
Научились:
вычислять количество перестановок, размещений и сочетаний;
решать простейшие комбинаторные задачи.
Подведем итоги
Слайд 43
Рефлексия
Сегодня я узнал(а) .......
Было трудно…
Я понял(а), что…
Я научился(ась)…
Я смог(ла)…
Было интересно узнать, что…
Меня удивило…
Мне захотелось…
Слайд 44Выберите смайлик, который соответствует Вашему настроению в конце урока
Спасибо за урок!
Мне
было очень трудно. Я ничего
не понял.
не понял.
Мне всё удалось!
Мне не все удалось, придется дома подольше посидеть…
