- Главная
- Разное
- Образование
- Спорт
- Естествознание
- Природоведение
- Религиоведение
- Французский язык
- Черчение
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, фоны, картинки для презентаций
- Экология
- Экономика
Презентация, доклад на тему Свойства функции
Содержание
- 1. Свойства функции
- 2. Возрастание и убывание функции
- 3. Рассмотрим график функции y=f(x).
- 4. Определение 1 Функция называется монотонно возрастающей (или
- 5. Убывание функцииРассмотрим график функции y=g(x). Для
- 6. Функция y = g ( x )
- 7. Промежутки возрастания и убывания называются промежутками монотонности функции. Промежутки монотонности
- 8. Рассмотрим график функции y=k. График функции
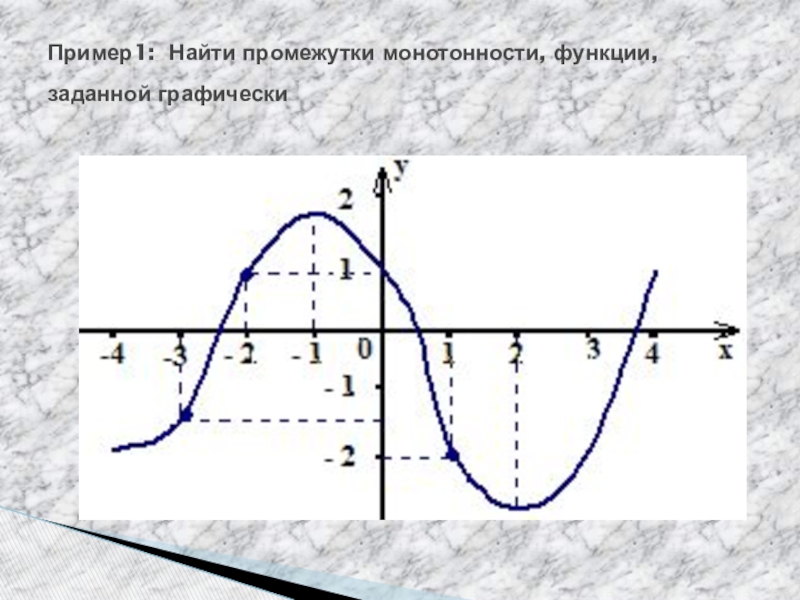
- 9. Пример1: Найти промежутки монотонности, функции, заданной графически
- 10. Решение1) Выберем два произвольных значения x1 <
- 11. Экстремумы функции
- 12. ВведениеРассмотрим график функции y=h(x). Область определения
- 13. Окрестность точки При исследовании поведения функции вблизи
- 14. Точка максимума Если взять точки из окрестности
- 15. Точка минимума Рассмотрим точки из окрестности точки
- 16. Экстремумы функции Точки максимума и минимума называются
Возрастание и убывание функции
Слайд 1СВОЙСТВА ФУНКЦИИ
Автор презентации:
учитель математики
МБОУ СОШ №12
Кравченко Н.И.
Ст. Ленинградская
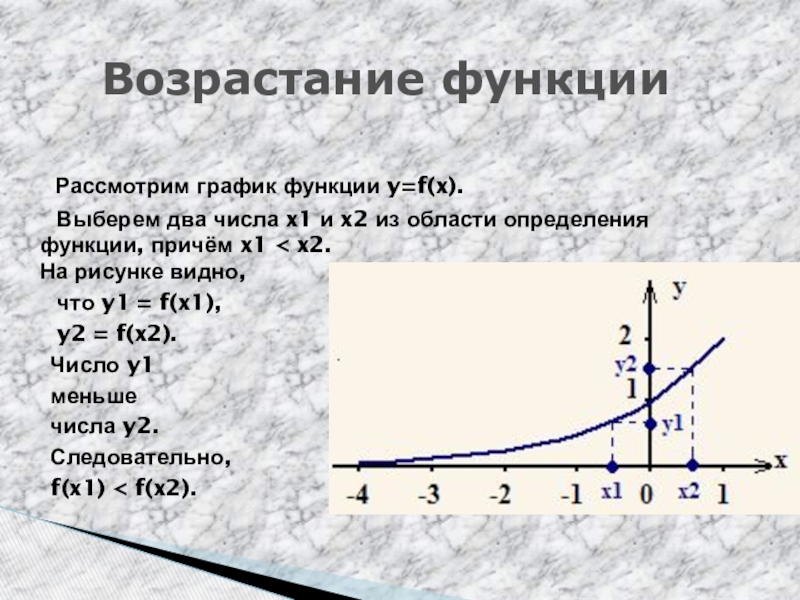
Слайд 3 Рассмотрим график функции y=f(x).
Выберем два числа x1
и x2 из области определения функции, причём x1 < x2.
На рисунке видно,
что y1 = f(x1),
y2 = f(x2).
Число y1
меньше
числа y2.
Следовательно,
f(x1) < f(x2).
что y1 = f(x1),
y2 = f(x2).
Число y1
меньше
числа y2.
Следовательно,
f(x1) < f(x2).
Возрастание функции
Слайд 4Определение 1
Функция называется монотонно возрастающей
(или просто возрастающей) в интервале
a ≤ x ≤ b,
если из условия x1 < x2 следует, что f ( x1)< f ( x2 ).
При этом a ≤ x1 ≤ b, a ≤ x2 ≤ b.
Другими словами, функция называется монотонно возрастающей в некотором интервале, если из двух произвольных значений аргумента, взятых из этого интервала, большему значению аргумента соответствует большее значение функции.
Примечание: представьте, что двигаясь по оси OX
слева направо, по графику функции движемся вверх.
если из условия x1 < x2 следует, что f ( x1)< f ( x2 ).
При этом a ≤ x1 ≤ b, a ≤ x2 ≤ b.
Другими словами, функция называется монотонно возрастающей в некотором интервале, если из двух произвольных значений аргумента, взятых из этого интервала, большему значению аргумента соответствует большее значение функции.
Примечание: представьте, что двигаясь по оси OX
слева направо, по графику функции движемся вверх.
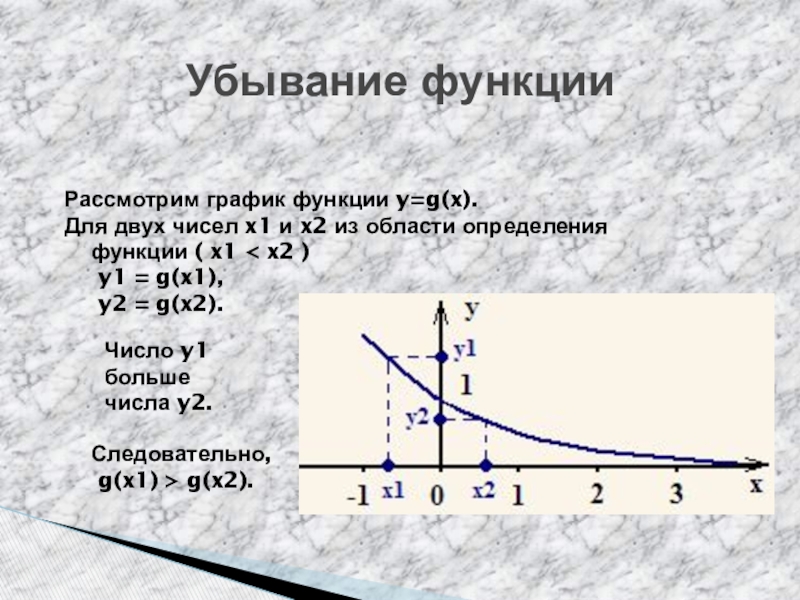
Слайд 5Убывание функции
Рассмотрим график функции y=g(x).
Для двух чисел x1 и
x2 из области определения
функции ( x1 < x2 )
y1 = g(x1),
y2 = g(x2).
Число y1
больше
числа y2.
Следовательно,
g(x1) > g(x2).
функции ( x1 < x2 )
y1 = g(x1),
y2 = g(x2).
Число y1
больше
числа y2.
Следовательно,
g(x1) > g(x2).
Слайд 6Функция y = g ( x ) называется монотонно убывающей
(или
просто убывающей) в интервале a = < x < = b,
если из условия x2 > x1 следует, что g( x2 ) < g( x1 ).
При этом а = < x1 < = b, a = < x2
Другими словами, функция называется монотонно убывающей в некотором интервале, если из двух произвольных значений аргумента, взятых из этого интервала, большему соответствует меньшее значение функции.
Примечание: представьте, что двигаясь по оси OX слева направо, по графику функции движемся вниз.
если из условия x2 > x1 следует, что g( x2 ) < g( x1 ).
При этом а = < x1 < = b, a = < x2
Другими словами, функция называется монотонно убывающей в некотором интервале, если из двух произвольных значений аргумента, взятых из этого интервала, большему соответствует меньшее значение функции.
Примечание: представьте, что двигаясь по оси OX слева направо, по графику функции движемся вниз.
Определение 2
Слайд 7 Промежутки возрастания и убывания называются промежутками монотонности функции.
Промежутки
монотонности
Слайд 8Рассмотрим график функции y=k.
График функции - это прямая, параллельная
оси OX.
Очевидно, что эта функция не возрастающая и не
убывающая на всём множестве действительных
чисел.
Определение 3.
Функция, не
возрастающая
и не убывающая
на всей области
определения
Называется
постоянной.
Очевидно, что эта функция не возрастающая и не
убывающая на всём множестве действительных
чисел.
Определение 3.
Функция, не
возрастающая
и не убывающая
на всей области
определения
Называется
постоянной.
Определение постоянной функции
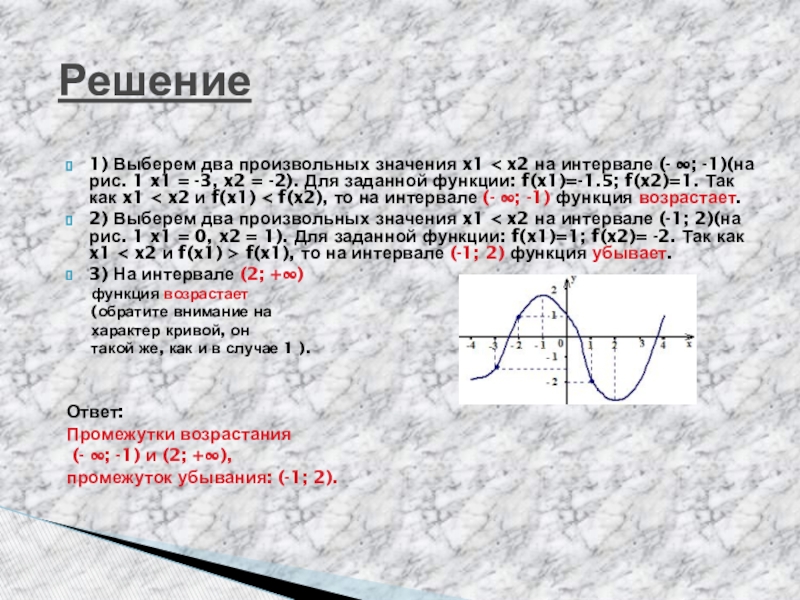
Слайд 10Решение
1) Выберем два произвольных значения x1 < x2 на интервале (-
∞; -1)(на рис. 1 x1 = -3, x2 = -2). Для заданной функции: f(x1)=-1.5; f(x2)=1. Так как x1 < x2 и f(x1) < f(x2), то на интервале (- ∞; -1) функция возрастает.
2) Выберем два произвольных значения x1 < x2 на интервале (-1; 2)(на рис. 1 x1 = 0, x2 = 1). Для заданной функции: f(x1)=1; f(x2)= -2. Так как x1 < x2 и f(x1) > f(x1), то на интервале (-1; 2) функция убывает.
3) На интервале (2; +∞)
функция возрастает
(обратите внимание на
характер кривой, он
такой же, как и в случае 1 ).
Ответ:
Промежутки возрастания
(- ∞; -1) и (2; +∞),
промежуток убывания: (-1; 2).
2) Выберем два произвольных значения x1 < x2 на интервале (-1; 2)(на рис. 1 x1 = 0, x2 = 1). Для заданной функции: f(x1)=1; f(x2)= -2. Так как x1 < x2 и f(x1) > f(x1), то на интервале (-1; 2) функция убывает.
3) На интервале (2; +∞)
функция возрастает
(обратите внимание на
характер кривой, он
такой же, как и в случае 1 ).
Ответ:
Промежутки возрастания
(- ∞; -1) и (2; +∞),
промежуток убывания: (-1; 2).
Слайд 12Введение
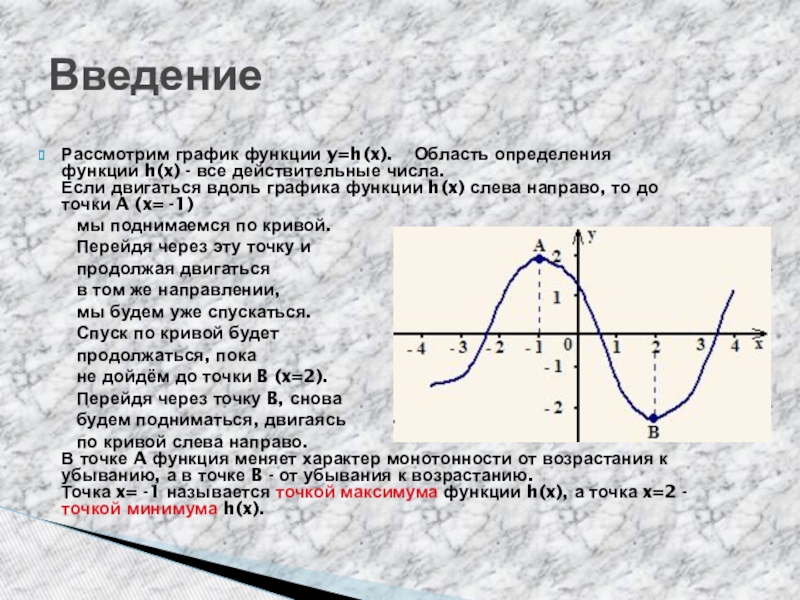
Рассмотрим график функции y=h(x). Область определения функции h(x) - все
действительные числа.
Если двигаться вдоль графика функции h(x) слева направо, то до точки A (x= -1)
мы поднимаемся по кривой.
Перейдя через эту точку и
продолжая двигаться
в том же направлении,
мы будем уже спускаться.
Спуск по кривой будет
продолжаться, пока
не дойдём до точки B (x=2).
Перейдя через точку B, снова
будем подниматься, двигаясь
по кривой слева направо. В точке A функция меняет характер монотонности от возрастания к убыванию, а в точке B - от убывания к возрастанию. Точка x= -1 называется точкой максимума функции h(x), а точка x=2 - точкой минимума h(x).
мы поднимаемся по кривой.
Перейдя через эту точку и
продолжая двигаться
в том же направлении,
мы будем уже спускаться.
Спуск по кривой будет
продолжаться, пока
не дойдём до точки B (x=2).
Перейдя через точку B, снова
будем подниматься, двигаясь
по кривой слева направо. В точке A функция меняет характер монотонности от возрастания к убыванию, а в точке B - от убывания к возрастанию. Точка x= -1 называется точкой максимума функции h(x), а точка x=2 - точкой минимума h(x).
Слайд 13Окрестность точки
При исследовании поведения функции вблизи некоторой точки удобно пользоваться
понятием окрестности.
Определение Окрестностью точки а называется любой интервал, содержащий эту точку. Например, интервал ( 2; 6 ) - одна из окрестностей точки 3, интервал ( - 3,3; - 2, 7 ) - окрестность точки - 3.
Определение Окрестностью точки а называется любой интервал, содержащий эту точку. Например, интервал ( 2; 6 ) - одна из окрестностей точки 3, интервал ( - 3,3; - 2, 7 ) - окрестность точки - 3.
Слайд 14Точка максимума
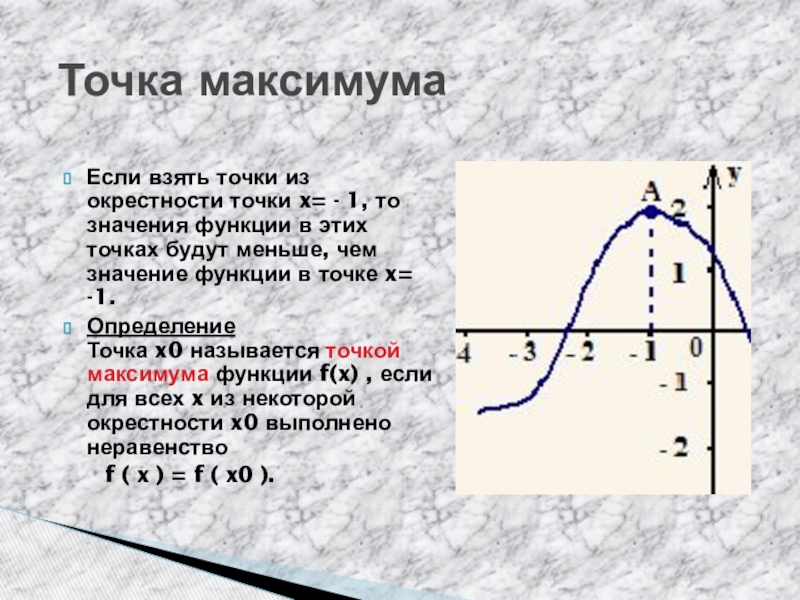
Если взять точки из окрестности точки x= - 1,
то значения функции в этих точках будут меньше, чем значение функции в точке x= -1.
Определение Точка x0 называется точкой максимума функции f(x) , если для всех x из некоторой окрестности x0 выполнено неравенство
f ( x ) = f ( x0 ).
Определение Точка x0 называется точкой максимума функции f(x) , если для всех x из некоторой окрестности x0 выполнено неравенство
f ( x ) = f ( x0 ).
Слайд 15Точка минимума
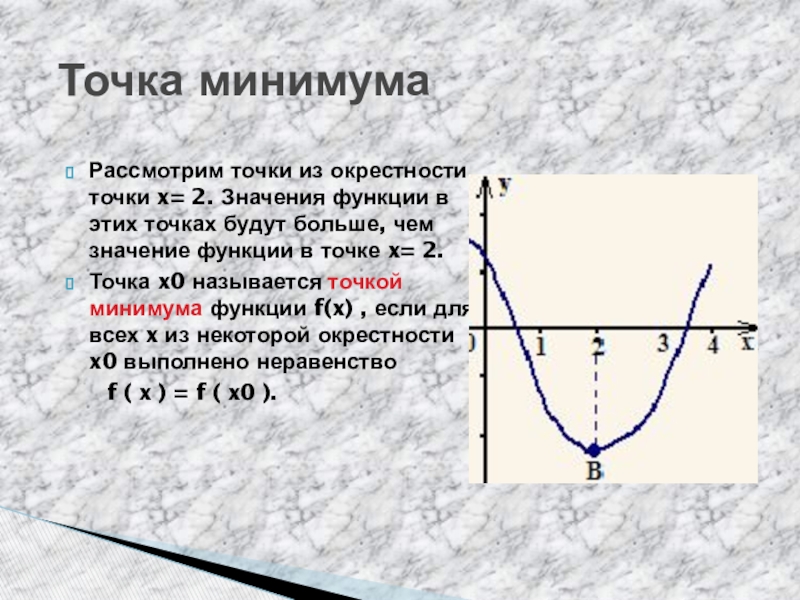
Рассмотрим точки из окрестности точки x= 2. Значения функции
в этих точках будут больше, чем значение функции в точке x= 2.
Точка x0 называется точкой минимума функции f(x) , если для всех x из некоторой окрестности x0 выполнено неравенство
f ( x ) = f ( x0 ).
Точка x0 называется точкой минимума функции f(x) , если для всех x из некоторой окрестности x0 выполнено неравенство
f ( x ) = f ( x0 ).
Слайд 16Экстремумы функции
Точки максимума и минимума называются точками экстремума функции и
обозначаются:
xmax, xmin.
Значения функции в этих точках называются экстремумами функции и обозначаются: ymax = f( xmax ), ymin = f( xmin ).
xmax, xmin.
Значения функции в этих точках называются экстремумами функции и обозначаются: ymax = f( xmax ), ymin = f( xmin ).