- Главная
- Разное
- Образование
- Спорт
- Естествознание
- Природоведение
- Религиоведение
- Французский язык
- Черчение
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, фоны, картинки для презентаций
- Экология
- Экономика
Презентация, доклад на тему Степень с натуральным показателем
Содержание
- 1. Степень с натуральным показателем
- 2. Что такое степень с натуральным показателемПод an,
- 3. Что такое степень с натуральным показателемВ своей
- 4. Что такое степень с натуральным показателем Современная
- 5. Что такое степень с натуральным показателемa n‒
- 6. Что такое степень с натуральным показателем4 ·
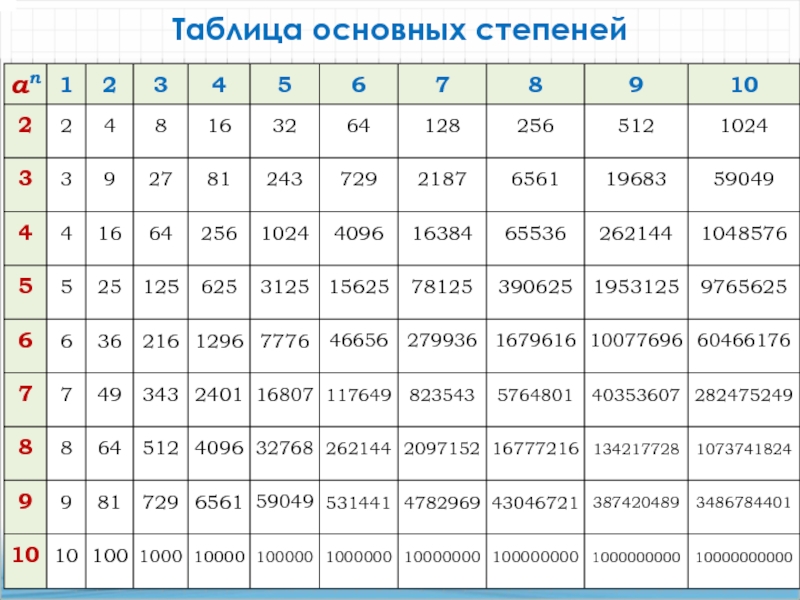
- 7. Таблица основных степеней
- 8. Свойства степени с натуральным показателем1. Если a
- 9. Свойства степени с натуральным показателем2. Если a
- 10. Свойства степени с натуральным показателем3. Для любого
- 11. Примеры: Свойства степени с натуральным показателем
- 12. Умножение и деление степеней с одинаковыми показателями n n n
- 13. Умножение и деление степеней с одинаковыми показателями n n n
- 14. Степень с нулевым показателемa 0 = 1чётный показательнечётный показатель
- 15. Алгебра 7 класс. Учебник / А.Г. Мордкович, Т.Н. Мишустина, Москва: Мнемозина, 2015г.https://ru.wikipedia.org/wiki/Диофант_Александрийский https://ru.wikipedia.org/wiki/Брахмагупта https://ru.wikipedia.org/wiki/Декарт,_Рене ДекартИспользованы ресурсы
Слайд 2Что такое степень с натуральным показателем
Под an, где n = 2,
Выражение an называют степенью, число а – основанием степени, число n – показателем степени.
3 · 3 · 3 · 3 · 3 =
7 · 7 · 7 · 7 · 7 · 7 · 7 · 7 =
х · х · х · х · х · х =
(c + b) · (c + b) · (c + b) · (c + b) =
35
78
х6
(c + b)4
a · a · a · a · a · a · a · … · a =
a n
n
Слайд 3Что такое степень с натуральным показателем
В своей знаменитой «Арифметике» Диофант Александрийский
«Все числа … состоят из некоторого количества единиц; ясно, что они продолжаются, увеличиваясь до бесконечности. … среди них находятся: квадраты, получающиеся от умножения некоторого числа самого на себя; это же число называется стороной квадрата, затем кубы, получающиеся от
умножения квадратов на их сторону, далее квадрато-квадраты – от умножения квадратов самих на себя, далее квадрато-кубы, получающиеся от умножения квадрата на куб его стороны, далее кубо-кубы – от умножения кубов самих на себя».
Слайд 4Что такое степень с натуральным показателем
Современная запись показателя степени введена Рене
В VII веке индийский математик Брахмагупта обозначал возведение в квадратную степень знаком व (от санскр. वर्ग – квадратное число).
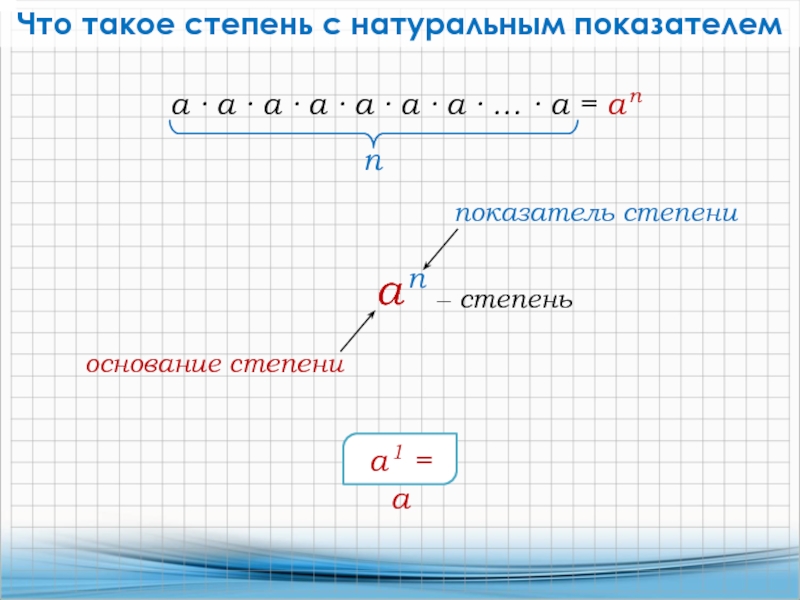
Слайд 5Что такое степень с натуральным показателем
a n
‒ степень
основание степени
показатель степени
a
a n
n
a 1 = а
Слайд 6Что такое степень с натуральным показателем
4 · 4 · 4 ·
9 · 9 · 9 · 9 · 9 · 9 · 9 =
(-5) · (-5) · (-5) · (-5) · (-5) · (-5) =
44 = 256
97 = 4 782 969
(-5)6 = 15 625
0 · 0 · 0 · 0 · 0 · 0 · 0 · … · 0 =
0 n = 0
n
Примеры:
1 · 1 · 1 · 1 · 1 · 1 · 1 · … · 1 =
1 n = 1
n
10 · 10 · 10 · 10 · 10 · … · 10 =
10 n = 1000…0
n
n нулей
Слайд 8 Свойства степени с натуральным показателем
1. Если a – любое число и
(3 · 3 · 3 · 3 · 3) · (3 · 3) =
35 · 32 =
(a · a · a · … · a) · (a · a · a · … · a) =
a n + k
5
3 5 + 2 = 37 = 2 187
2
a n · ak =
n
k
an · ak = an + k
Слайд 9 Свойства степени с натуральным показателем
2. Если a ≠ 0 и n,
3 · 3 · 3 · 3 · 3
3 · 3
35 : 32 =
a · a · a · … · a
a · a · … · a
= a n – k
= 3 5 – 2 = 33 = 27
a n : ak =
an : ak = an – k
Слайд 10 Свойства степени с натуральным показателем
3. Для любого числа a и любых
(3 · 3 · 3 · 3 · 3) · (3 · 3 · 3 · 3 · 3) =
(35)2 =
(a · a · … · a)·(a · a · … · a)· … ·(a · a · … · a) =
= a n + n + n + … + n =
5
= 3 5 · 35 = 35·2 = 310 = 59 049
5
(a n)k =
n
k
(an)k = ank
n
n
k
ank
Слайд 15Алгебра 7 класс. Учебник / А.Г. Мордкович, Т.Н. Мишустина, Москва: Мнемозина,
https://ru.wikipedia.org/wiki/Диофант_Александрийский
https://ru.wikipedia.org/wiki/Брахмагупта
https://ru.wikipedia.org/wiki/Декарт,_Рене Декарт
Использованы ресурсы