- Главная
- Разное
- Образование
- Спорт
- Естествознание
- Природоведение
- Религиоведение
- Французский язык
- Черчение
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, фоны, картинки для презентаций
- Экология
- Экономика
Презентация, доклад на тему Софизмы и парадоксы в математике
Содержание
- 1. Софизмы и парадоксы в математике
- 2. "Предмет математики настолько
- 3. Цель работы: Познакомиться с софизмами, показать
- 4. Задачи:1.Дать определение понятиям «софизм» и «парадокс», узнать
- 5. Слайд 5
- 6. Основные создатели софизмов – древнегреческие
- 7. Экскурс в историюСофистами называли группу древнегреческих философов
- 8. Математические софизмыРазбор и решение нестандартных математических задач
- 9. I. Алгебраические софизмыАлгебра — один из больших
- 10. 1) «Один рубль не
- 11. Ошибка, допущенная в этом софизме, состоит
- 12. Геометрические софизмы Геометрические софизмы – это
- 13. «Через точку на прямую можно опустить два
- 14. Арифметические софизмы. Арифметика - (греч.
- 15. «Дважды два - пять!»
- 16. Логические софизмы Раскрывая данный вопрос,
- 17. «Ахиллес и черепаха»Представляет собой апорию о движении. Как
- 18. Многообразие парадоксов и их причины Парадоксы
- 19. 1. Парадокс Банаха - Тарского Парадокс
- 20. О математических софизмах и парадоксах
Слайд 1«Софизмы и парадоксы в математике»
Секция: математика
Выполнили: Павлюченко Дарья,
Слайд 2
"Предмет математики настолько серьезен,
что полезно не упускать
Математический софизм – удивительное утверждение, в доказательстве которого кроются незаметные и довольно тонкие ошибки.
Софизмы имеют четкое логическое объяснение. Кроме того, с математическими софизмами мы встречаемся намного чаще, чем с обычными. Поиск заключенных в софизме ошибок, ясное понимание их причин ведут к осмысленному постижению математики и, кроме того, показывает, что математика – это живая наука.
Введение
Слайд 3Цель работы:
Познакомиться с софизмами, показать значимость математических софизмов
при изучении
Слайд 4Задачи:
1.Дать определение понятиям «софизм» и «парадокс», узнать в чём их отличие;
2.Классифицировать
3.Понять, как найти ошибку в софизмах.
Слайд 5
Понятие софизма
Софизм (от
1.Сложное рассуждение, иногда намеренно
запутанное с целью показать умственное
превосходство или ввести в заблуждение;
2.Нестандартная задача, как правило , имеющая
несколько решений;
3.Приём обучения и метод исследования, введённый
древнегреческими софистами;
4.Ошибочное рассуждение, неправильный аргумент.
Слайд 6 Основные создатели софизмов – древнегреческие ученые-философы, но, тем не
Слайд 7Экскурс в историю
Софистами называли группу древнегреческих философов 4-5 века до н.э.,
Слайд 8Математические софизмы
Разбор и решение нестандартных математических задач помогает развивать смекалку и
Слайд 9I. Алгебраические софизмы
Алгебра — один из больших разделов математики, принадлежащий наряду
Слайд 10
1) «Один рубль не равен ста копейкам»
Известно, что
Слайд 11 Ошибка, допущенная в этом софизме, состоит в нарушении правил действия с
Слайд 12Геометрические софизмы
Геометрические софизмы – это умозаключения или рассуждения, обосновывающие
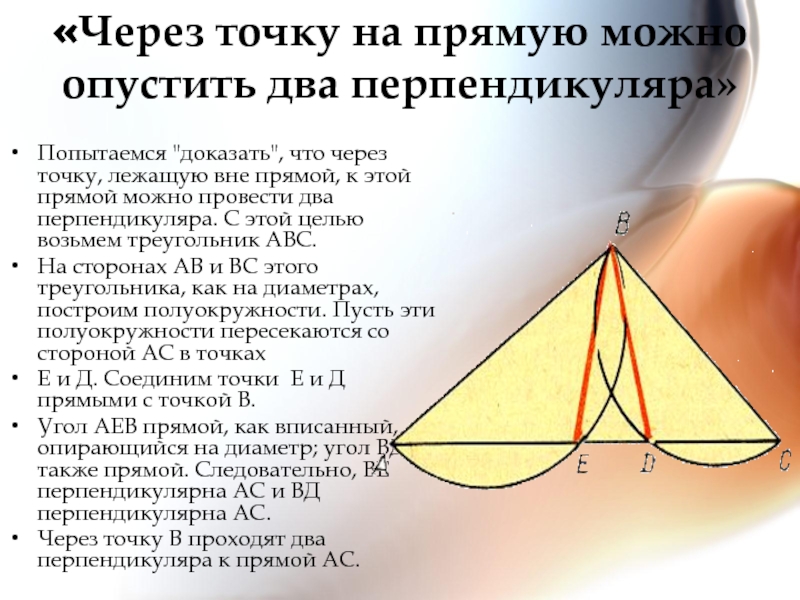
Слайд 13«Через точку на прямую можно опустить два перпендикуляра»
Попытаемся "доказать", что через
На сторонах АВ и ВС этого треугольника, как на диаметрах, построим полуокружности. Пусть эти полуокружности пересекаются со стороной АС в точках
Е и Д. Соединим точки Е и Д прямыми с точкой В.
Угол АЕВ прямой, как вписанный, опирающийся на диаметр; угол ВДС также прямой. Следовательно, ВЕ перпендикулярна АС и ВД перпендикулярна АС.
Через точку В проходят два перпендикуляра к прямой АС.
Слайд 14Арифметические софизмы.
Арифметика - (греч. arithmetika, от arithmys —
Арифметические софизмы – это числовые выражения, имеющие неточность или ошибку, не заметную с первого взгляда.
Слайд 15 «Дважды два - пять!»
Возьмем в качестве исходного
После вынесения за скобки общего множителя из каждой части равенства будем иметь:
4∙(1:1)=5∙(1:1)
или
(2∙2)(1:1)=5(1:1)
Наконец, зная, что 1:1=1, мы из предыдущего получаем:
2∙2=5
Где ошибка?
Нельзя выносить множитель за скобки так, как было сделано. 4∙(1:1)=5∙(1:1)
Можно так 4 (1:4) и 5 (1:5).
Слайд 16Логические софизмы
Раскрывая данный вопрос, необходимо сказать, что любой софизм
Слайд 17«Ахиллес и черепаха»
Представляет собой апорию о движении. Как известно, Ахиллес — это
Слайд 18Многообразие парадоксов и их причины
Парадоксы – это неожиданные утверждения,
Слайд 191. Парадокс Банаха - Тарского
Парадокс удвоения шара, говорит, что
Слайд 20 О математических софизмах и парадоксах можно говорить бесконечно много,
Некоторые софизмы приходилось разбирать по нескольку раз, чтобы действительно в них разобраться, некоторые же наоборот, казались очень простыми. Исторические сведения о софистике и софистах помогли нам разобраться, откуда же все-таки началась история софизмов.
Благодаря софизмам и парадоксам можно научиться искать ошибки в рассуждениях других, научится грамотно строить свои рассуждения и логические объяснения.