- Главная
- Разное
- Образование
- Спорт
- Естествознание
- Природоведение
- Религиоведение
- Французский язык
- Черчение
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, фоны, картинки для презентаций
- Экология
- Экономика
Презентация, доклад на тему Системы уравнений. презентация к уроку
Содержание
- 1. Системы уравнений. презентация к уроку
- 2. Системы уравнений с двумя переменными. Ребята, давайте
- 3. Системы уравнений с двумя переменными. Решение обычно
- 4. Системы уравнений с двумя переменными. Решим пару
- 5. Системы уравнений с двумя переменными. Решить систему уравнений: Решение. Давайте
- 6. Неравенства с двумя переменными. Ребята, теперь давайте перейдем
- 7. Неравенства с двумя переменными. Для решения неравенств
- 8. Неравенства с двумя переменными. После того, как построили
- 9. Неравенства с двумя переменными.Пример. Решить неравенство: Построим
- 10. Система неравенств с двумя переменными.Если требуется найти
- 11. Система неравенств с двумя переменными.Пример.Решить систему неравенств:Решение:Давайте
- 12. Система неравенств с двумя переменными.Построим график второго
- 13. Системы уравнений. Понятия..Задачи для самостоятельного решения:1. Решить
Слайд 1Занимательная математика
Алгебра
9 класс.
Урок на тему:
Системы
Уравнений с двумя
переменными.
Графический метод.
Слайд 2Системы уравнений с двумя переменными.
Ребята, давайте остановимся на такой теме
Определение. Если нужно найти пару чисел (x;y), таких что они одновременно удовлетворяют рациональным уравнениям: p(x;y)=0 и u(x;y)=0, то принято говорить, что они образуют систему уравнений:
Решение системы – это пара чисел, которая удовлетворяет сразу двум нашим уравнениям.
Решить систему – это значит найти все ее решения, или убедиться, что общих решений у исходных уравнений нет.
Слайд 3Системы уравнений с двумя переменными.
Решение обычно записывают в круглых скобках,
Для решения систем уравнений используют различные методы: метод подстановки, метод сложения, замены переменой и графический метод. Все способы решения мы с вами изучим позже.
Переменные в системе можно обозначать любыми буквами, чаще всего обозначают латинскими буквами, но стоит помнить, что первой записывают переменную, которая встречается раньше в алфавите.
Слайд 4Системы уравнений с двумя переменными.
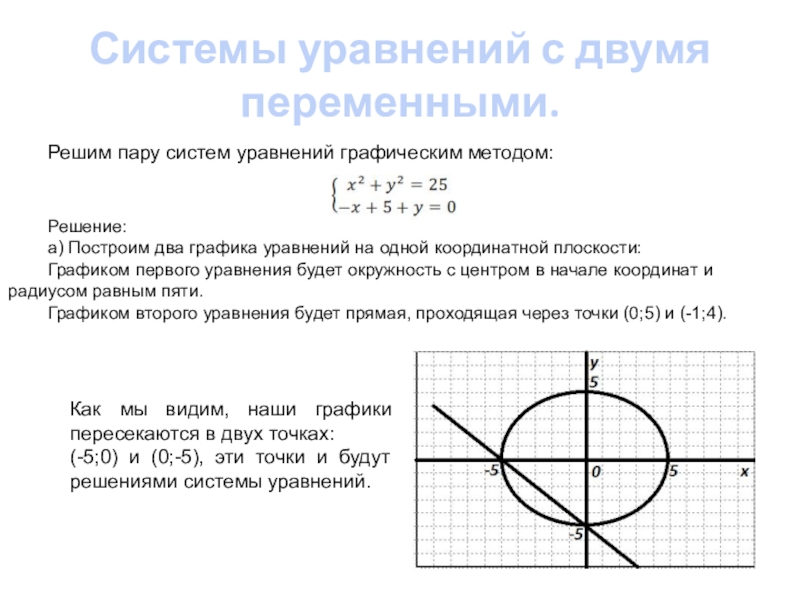
Решим пару систем уравнений графическим методом:
Решение:
а)
Графиком первого уравнения будет окружность с центром в начале координат и радиусом равным пяти.
Графиком второго уравнения будет прямая, проходящая через точки (0;5) и (-1;4).
Как мы видим, наши графики пересекаются в двух точках:
(-5;0) и (0;-5), эти точки и будут решениями системы уравнений.
Слайд 5Системы уравнений с двумя переменными.
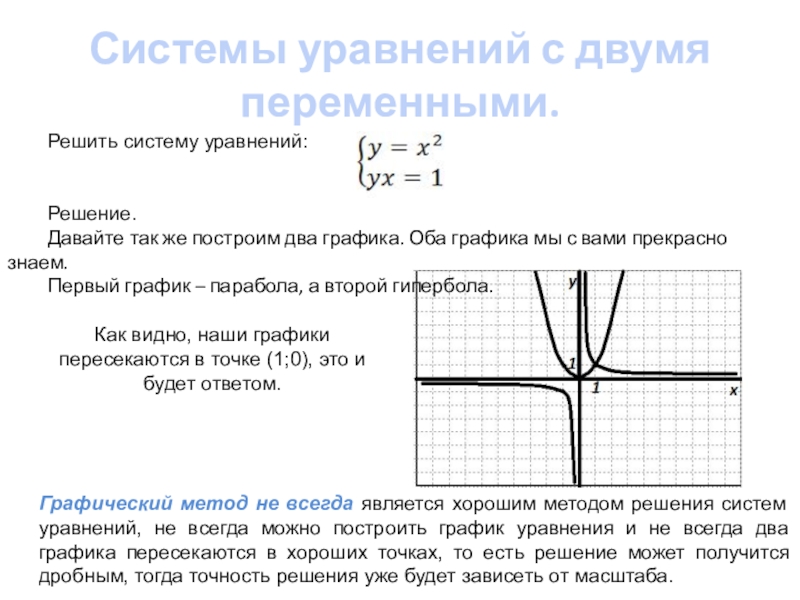
Решить систему уравнений:
Решение.
Давайте так же построим два
Первый график – парабола, а второй гипербола.
Как видно, наши графики пересекаются в точке (1;0), это и будет ответом.
Графический метод не всегда является хорошим методом решения систем уравнений, не всегда можно построить график уравнения и не всегда два графика пересекаются в хороших точках, то есть решение может получится дробным, тогда точность решения уже будет зависеть от масштаба.
Слайд 6Неравенства с двумя переменными.
Ребята, теперь давайте перейдем к теме неравенства и
Решением рационального неравенства u(x;y)>0 – называется пара чисел (x;y), такая, что неравенство становится верным числовым выражением.
Например, рассмотрим неравенство 2х+2y>0 при х=1 и y=1
наше неравенство верно.
Тогда пара чисел (1;1) – решение нашего неравенства. Но, наша пара чисел, лишь только частное решение, а как, же найти общее решение?
Слайд 7Неравенства с двумя переменными.
Для решения неравенств с двумя переменными, оказалось,
Давайте посмотрим как можно решить наше неравенство, с помощью графика: 2х+2y>0
Графиком уравнения 2х+2y=0 – будет прямая проходящая через начало координат и точку (-1;-1). Давайте построим наш график:
Приведем исходное неравенство к виду
y>-x, тогда, очевидно, решением неравенства будет вся область находящаяся выше нашей прямой.
Слайд 8Неравенства с двумя переменными.
После того, как построили график уравнения, для решения
.
Слайд 9Неравенства с двумя переменными.
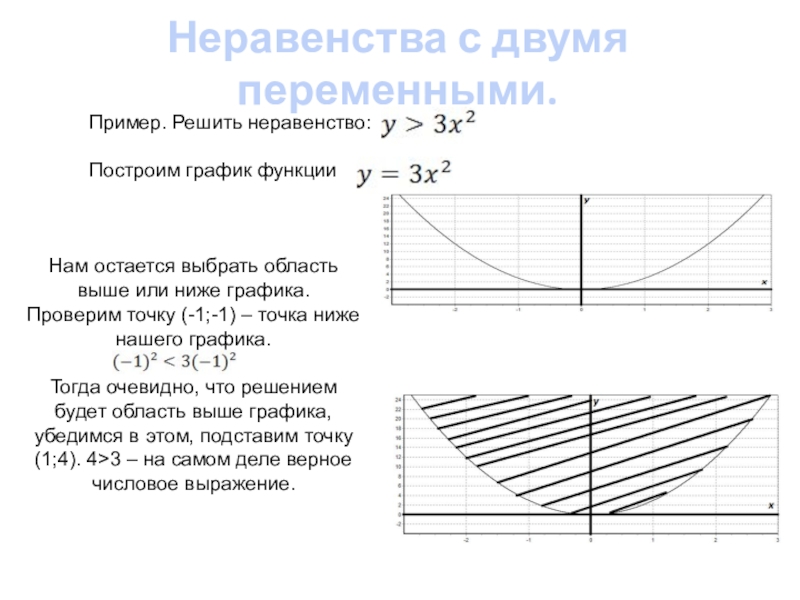
Пример. Решить неравенство:
Построим график функции
.
Нам
Проверим точку (-1;-1) – точка ниже нашего графика.
Тогда очевидно, что решением будет область выше графика, убедимся в этом, подставим точку (1;4). 4>3 – на самом деле верное числовое выражение.
Слайд 10Система неравенств с двумя переменными.
Если требуется найти два числа x и
Решение системы – это пара чисел, которая удовлетворяет сразу двум нашим неравенствам.
.
Слайд 11Система неравенств с двумя переменными.
Пример.
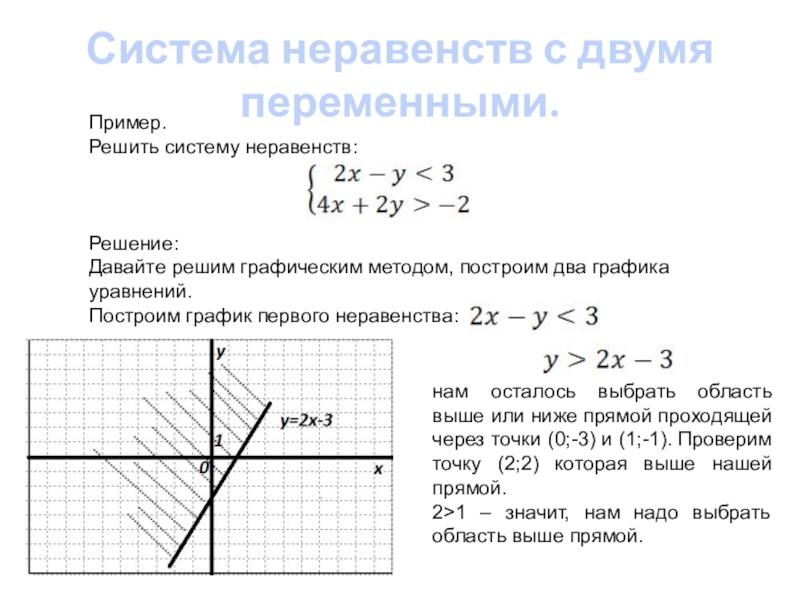
Решить систему неравенств:
Решение:
Давайте решим графическим методом, построим
Построим график первого неравенства:
.
нам осталось выбрать область выше или ниже прямой проходящей через точки (0;-3) и (1;-1). Проверим точку (2;2) которая выше нашей прямой.
2>1 – значит, нам надо выбрать область выше прямой.
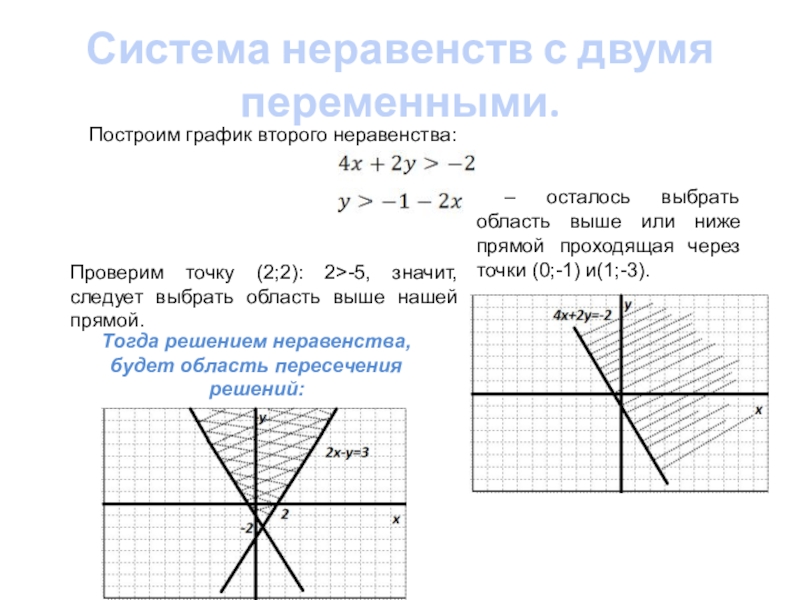
Слайд 12Система неравенств с двумя переменными.
Построим график второго неравенства:
.
– осталось
Проверим точку (2;2): 2>-5, значит, следует выбрать область выше нашей прямой.
Тогда решением неравенства, будет область пересечения решений:
Слайд 13Системы уравнений. Понятия.
.
Задачи для самостоятельного решения:
1. Решить систему уравнений графическим методом:
2.
3. Решить систему неравенств графическим методом:
а) б)