- Главная
- Разное
- Образование
- Спорт
- Естествознание
- Природоведение
- Религиоведение
- Французский язык
- Черчение
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, фоны, картинки для презентаций
- Экология
- Экономика
Презентация, доклад на тему Решение простейших тригонометрических уравнений. Учебное пособие к теме.
Содержание
- 1. Решение простейших тригонометрических уравнений. Учебное пособие к теме.
- 2. Девиз « Не делай никогда того, чего
- 3. Цели урока: Образовательные:Актуализировать знания учащихся по теме «Решение
- 4. Развивающие:Содействовать развитию у учащихся мыслительных операций: умение
- 5. Воспитательные: Вырабатывать внимание, самостоятельность при работе
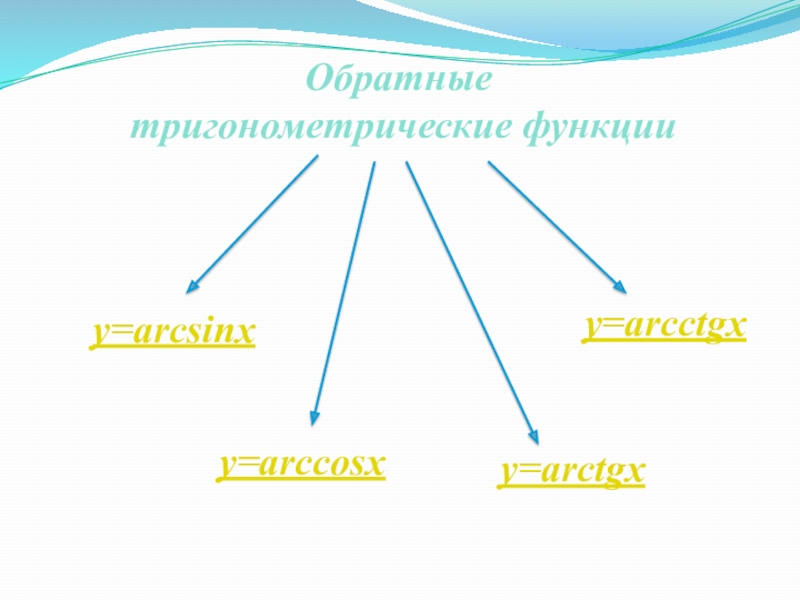
- 6. Обратные тригонометрические функцииу=arcsinxу=arccosxу=arctgxу=arcctgx
- 7. Арксинусом числа а называют такое число из
- 8. П0arccos аАрккосинусом числа а называют такое число
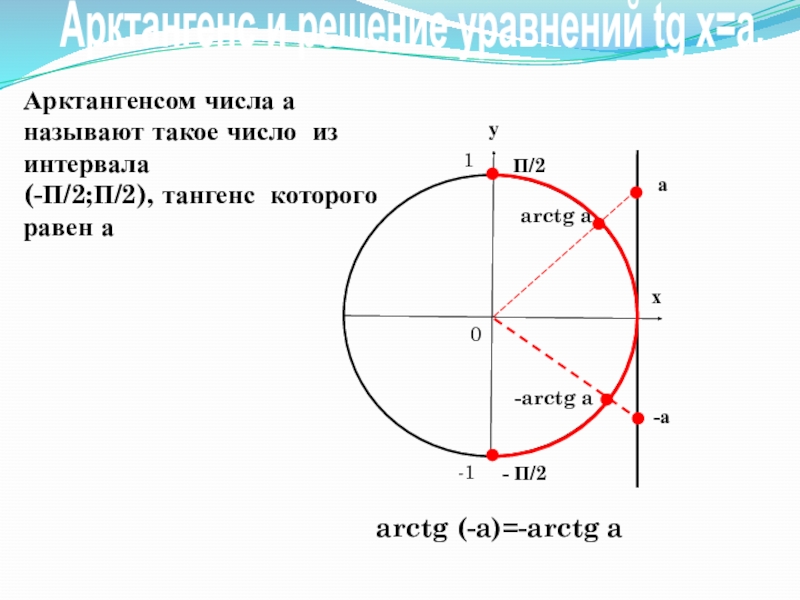
- 9. Арктангенсом числа а называют такое число из
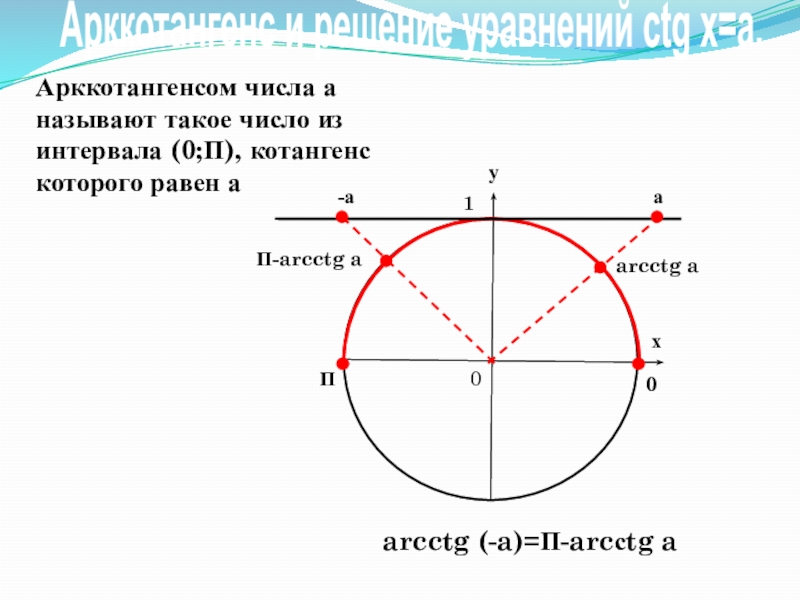
- 10. ух01П0Арккотангенсом числа а называют такое число из
- 11. Определение Уравнения с неизвестной переменной,
- 12. Формулы корней простейших тригонометрических уравнений
- 13. Уравнение переносом слагаемого и делением обеих частей легко сводится к простейшему.Разделим обе части на 4.О:tПримеры уравнений.
- 14. Ответ :Уравнение уже имеет простейший видЭто частный
- 15. tg (3x + π/4 ) +1 =
- 16. Слайд 16
- 17. Свойства аркфункций
- 18. Самостоятельная работа обучающего характера
- 19. Реши сам Группа 1
- 20. Кодовое словоГруппа 1
- 21. Фронтальным опросом вместе с учащимися подводятся итоги
Слайд 3Цели урока:
Образовательные:
Актуализировать знания учащихся по теме «Решение простейших тригонометрических уравнений» и
Повторить, углубить, обобщить и систематизировать приобретенные знания по теме «Обратные тригонометрические уравнения» для дальнейшего использования при решении тригонометрических уравнений.
Слайд 4Развивающие:
Содействовать развитию у учащихся мыслительных операций: умение анализировать, синтезировать, сравнивать;
Формировать и
Отрабатывать навыки самооценивания знаний и умений, выбора задания, соответствующего их уровню развития.
Слайд 5 Воспитательные:
Вырабатывать внимание, самостоятельность при работе на уроке;
Способствовать формированию активности
работоспособности;
Развивать интерес к урокам
математики.
Слайд 7Арксинусом числа
а называют такое число из отрезка
[- П/2;
arcsin а
П/2
- П/2
а
arcsin (-a)=-arcsin a
-а
-arcsin а
Арксинус и решение уравнений sin x=a.
Слайд 8П
0
arccos а
Арккосинусом числа а называют такое число из промежутка
[0;П
а
arccos (-a)=П-arccos a
-а
П-arccos a
Арккосинус и решение уравнений соs x=a.
Слайд 9Арктангенсом числа а называют такое число из интервала
(-П/2;П/2), тангенс которого
arctg a
а
П/2
- П/2
arctg (-a)=-arctg a
-а
-arctg a
Арктангенс и решение уравнений tg x=a.
Слайд 10у
х
0
1
П
0
Арккотангенсом числа а называют такое число из интервала (0;П), котангенс которого
-а
arcctg a
arcctg (-a)=П-arcсtg a
а
П-arcctg a
Арккотангенс и решение уравнений сtg x=a.
Слайд 11
Определение
Уравнения с неизвестной переменной, заданной в виде аргумента тригонометрической функции,
Решить тригонометрическое уравнение – значит найти значения аргумента, приводящие данное уравнение в верное тождество.
Простейшими тригонометрическими уравнениями называют уравнения вида cos x=a, sin x=a, tg x= a, ctg x=a. В этих уравнениях переменная находится под знаком тригонометрической функции, а – данное число.
Слайд 13Уравнение переносом слагаемого и делением обеих частей легко сводится к простейшему.
Разделим
О:
t
Примеры уравнений.
Слайд 14Ответ :
Уравнение уже имеет простейший
вид
Это частный вид
уравнения cos t=a
Примеры уравнений.
Слайд 15tg (3x + π/4 ) +1 = 0.
РЕШЕНИЕ:
tg (3x + π/4
3x + π/4 = -π/4 + πn, nЄZ;
3x = -π/4 - π/4 + πn, nЄZ;
3x = -π/2 + πn, nЄZ;
x = -π/6 + π/3n, nЄZ;
ОТВЕТ: x = -π/6 + π/3n, nЄZ.





![Решение простейших тригонометрических уравнений. Учебное пособие к теме. Арксинусом числа а называют такое число из отрезка [- П/2; П/2], Арксинусом числа а называют такое число из отрезка [- П/2; П/2], синус которого равен а.arcsin аП/2- П/2аarcsin](/img/thumbs/677fd2946ec1f5ab6116e602ee4611bd-800x.jpg)
![Решение простейших тригонометрических уравнений. Учебное пособие к теме. П0arccos аАрккосинусом числа а называют такое число из промежутка [0;П ], П0arccos аАрккосинусом числа а называют такое число из промежутка [0;П ], косинус которого равен ааarccos (-a)=П-arccos a-аП-arccos](/img/thumbs/df34a17dfe464b3b8c3902a25cd1f0ae-800x.jpg)