- Главная
- Разное
- Образование
- Спорт
- Естествознание
- Природоведение
- Религиоведение
- Французский язык
- Черчение
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, фоны, картинки для презентаций
- Экология
- Экономика
Презентация, доклад на тему Решение квадратных уравнений (8 класс)
Содержание
- 1. Решение квадратных уравнений (8 класс)
- 2. Человеку, изучающему алгебру, часто полезнее решить одну
- 3. — систематизировать различные способы решения квадратных уравнений, дать
- 4. Методы решения квадратных уравнений были известны еще
- 5. Для решения уравнения х2 + 10х =
- 6. А вот как решал эту же задачу
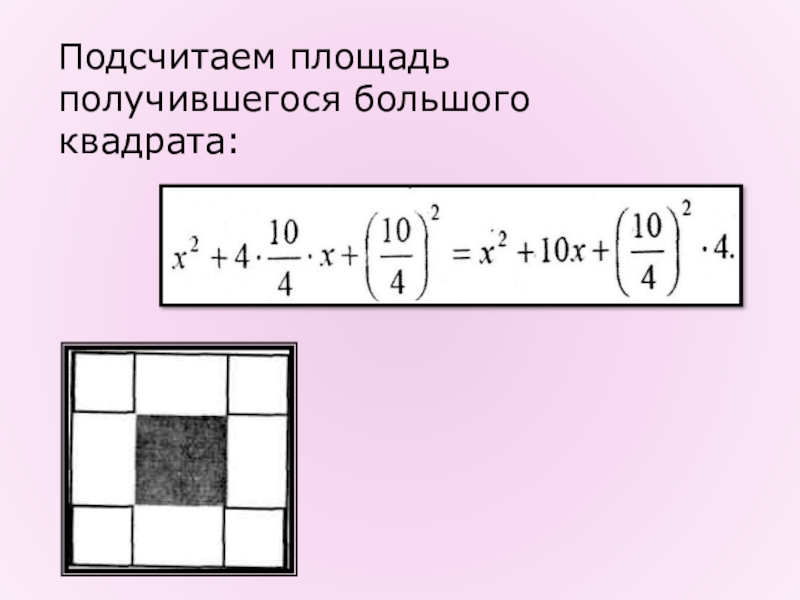
- 7. Подсчитаем площадь получившегося большого квадрата:
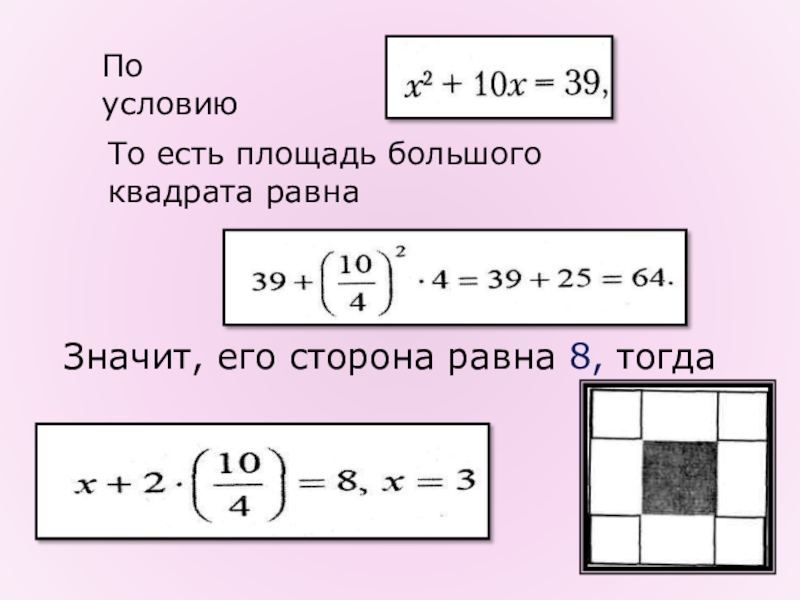
- 8. По условию То есть площадь большого квадрата равнаЗначит, его сторона равна 8, тогда
- 9. В III в. н. э. квадратное уравнение
- 10. И если половину разности — z прибавить
- 11. Попытаемся решить квадратное уравнение х2 + 10х
- 12. Неполные квадратные уравнения и частные виды полных
- 13. После трудов немецкого математика М. Штифеля (1487-1567
- 14. Франсуа Виет родился в 1540 г. во
- 15. Именно с 1591 г. мы пользуемся формулами
- 16. Следует отметить, что второй коэффициент в данном
- 17. Данное уравнение можно решить, используя теорему, обратную теореме Виета.
- 18. Существуют ли другие способы решения квадратных уравнений?Квадратные
- 19. Приведите примеры уравнений, решаемых с применением второго утверждения.
- 20. В учебнике мы встречаем задания, где четко
- 21. Известно, что учет населения проводился в Египте
- 22. На основе статистических данных можно выделить регионы
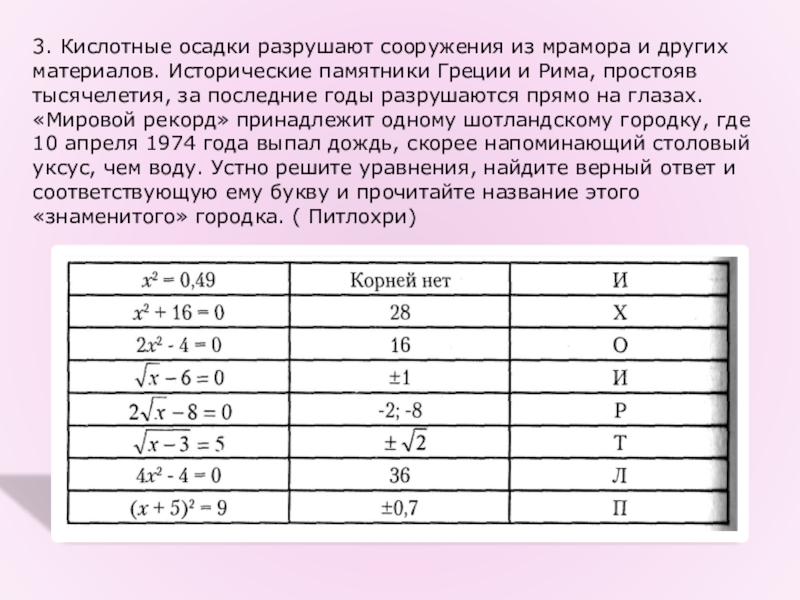
- 23. 3. Кислотные осадки разрушают сооружения из мрамора
Человеку, изучающему алгебру, часто полезнее решить одну и ту же задачу тремя различными способами, чем решать три-четыре различные задачи. Решая одну задачу различными способами, можно путем сравнения выяснить, какой из них короче и эффективнее. Так вырабатывается
Слайд 1Решение одной задачи
Решение квадратных уравнений
Учитель математики
МОУ «СОШ № 66»
Васильева Н.Д.
Слайд 2Человеку, изучающему алгебру, часто полезнее решить одну и ту же задачу
тремя различными способами, чем решать три-четыре различные задачи. Решая одну задачу различными способами, можно путем сравнения выяснить, какой из них короче и эффективнее. Так вырабатывается опыт.
У.У. Сойер
У.У. Сойер
История математики
Слайд 3— систематизировать различные способы решения квадратных уравнений, дать представление учащимся о важных
вехах истории развития математики;
— обучать поискам нескольких способов решения одной задачи и умению выбирать из них наиболее оригинальный, оптимальный;
— развивать навыки работы с дополнительной литературой, историческим материалом, формировать интерес к изучению математики.
— обучать поискам нескольких способов решения одной задачи и умению выбирать из них наиболее оригинальный, оптимальный;
— развивать навыки работы с дополнительной литературой, историческим материалом, формировать интерес к изучению математики.
Цели урока:
Слайд 4Методы решения квадратных уравнений были известны еще в древние
времена. Они излагались
в вавилонских рукописях царя Хаммурапи (XX в.
[до н. э.), в трудах древнегреческого математика Евклида (III в. до н. э.), в древних китайских и японских трактатах. Многие математики древности решали квадратные уравнения геометрическим способом: квадрат и 10 его корней равны 39.
[до н. э.), в трудах древнегреческого математика Евклида (III в. до н. э.), в древних китайских и японских трактатах. Многие математики древности решали квадратные уравнения геометрическим способом: квадрат и 10 его корней равны 39.
Слайд 5Для решения уравнения х2 + 10х = 39 поступали следующим образом.
Пусть АВ = х, ВС = 5, (10: 2). На стороне АС - АВ+ ВС построим квадрат, который разбивается на четыре части, как показано на рисунке. Очевидно, что сумма площадей I, II, и III частей равна х2 + 10х или 39. Если к этой площади прибавить площадь IV части, то 39 + 25 =64 - площадь всего квадрата. С другой стороны, эта же площадь равна (х+5)2. Следовательно, (х + 5)2 = 64.
х + 5 = 8, х = 3. Таким образом,
число 3 является корнем квадратного уравнения, ведь отрицательных чисел тогда не знали.
х + 5 = 8, х = 3. Таким образом,
число 3 является корнем квадратного уравнения, ведь отрицательных чисел тогда не знали.
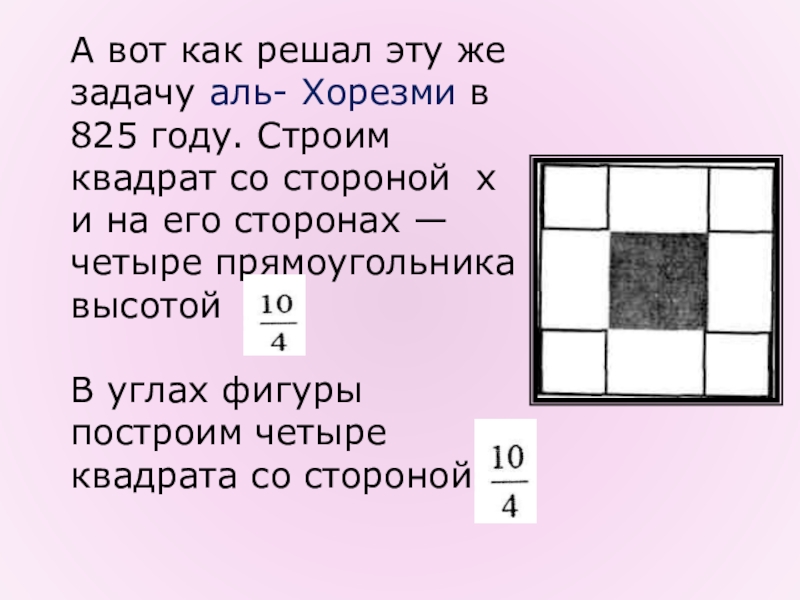
Слайд 6А вот как решал эту же задачу аль- Хорезми в 825
году. Строим квадрат со стороной х и на его сторонах —четыре прямоугольника высотой
В углах фигуры построим четыре квадрата со стороной
В углах фигуры построим четыре квадрата со стороной
Слайд 9В III в. н. э. квадратное уравнение х2 - 20х +
96 = 0 решал великий древнегреческий математик Диофант.
Пусть сумма двух чисел 20, а произведение 96. Положим, что разность этих чисел 2z. Так как их сумма 20, то если разделить ее пополам, каждая из полученных делением частей будет равна половине суммы, то есть 10.
Пусть сумма двух чисел 20, а произведение 96. Положим, что разность этих чисел 2z. Так как их сумма 20, то если разделить ее пополам, каждая из полученных делением частей будет равна половине суммы, то есть 10.
Слайд 10И если половину разности — z прибавить к одной из полученных
от деления половине и вычесть из другой, то опять получается сумма 20 и разность 2z.
Пусть большее из искомых чисел равно z+10, тогда меньшее — 10-z. Их сумма 20, разность 2z Произведение искомых чисел равно 96. Таким образом,
(10 +z)(10 -z) = 96,
100 - z2 = 96, z2 = 4,z= 2. Следовательно, большее число равно 12, меньшее 8.
Пусть большее из искомых чисел равно z+10, тогда меньшее — 10-z. Их сумма 20, разность 2z Произведение искомых чисел равно 96. Таким образом,
(10 +z)(10 -z) = 96,
100 - z2 = 96, z2 = 4,z= 2. Следовательно, большее число равно 12, меньшее 8.
Слайд 11Попытаемся решить квадратное уравнение
х2 + 10х = 39 методом Диофанта.
Пусть
х2+10х-39 = 0;
Положим разность искомых чисел 2z;
-5 — половина коэффициента при х с противоположным знаком;
Положим х = 2 – 5 или х = 2 + 5.
Тогда (z - 5)(z + 5) = 39,
z2 - 25 = 39,
z2 = 64, z = 8.
Отсюда, х1 = 8 - 5 = 3, х2 = 8 + 5 = 13. Полученные корни 13 и 3 «устроили» бы Диофанта, т.к. оба натуральные. Но, используя теорему Виета, видно, что
х, • х2 = -39, это означает, что корни должны быть разного знака. Следовательно, не каждое уравнение можно решить этим методом.
Положим разность искомых чисел 2z;
-5 — половина коэффициента при х с противоположным знаком;
Положим х = 2 – 5 или х = 2 + 5.
Тогда (z - 5)(z + 5) = 39,
z2 - 25 = 39,
z2 = 64, z = 8.
Отсюда, х1 = 8 - 5 = 3, х2 = 8 + 5 = 13. Полученные корни 13 и 3 «устроили» бы Диофанта, т.к. оба натуральные. Но, используя теорему Виета, видно, что
х, • х2 = -39, это означает, что корни должны быть разного знака. Следовательно, не каждое уравнение можно решить этим методом.
Слайд 12Неполные квадратные уравнения и частные виды полных квадратных уравнений умели решать
вавилоняне и египтяне (2 тыс. лет до н. э.). Некоторые виды квадратных уравнений решали и древнегреческие математики, используя геометрический подход. Примеры решения уравнений без обращения к геометрии дает Диофант Александрийский (III в. н. э.). В своем трактате хорезмский математик Мухаммед ал-Хорезми в 825 г. разъясняет приемы решения квадратных уравнений.
Слайд 13После трудов немецкого математика М. Штифеля (1487-1567 гг.), нидерландца А. Жирара
(1595-1632 гг.), Р. Декарта и И. Ньютона, способ решения квадратных уравнений принял современный вид. А в 1591 г. Ф. Виет вывел формулы, выражающие зависимость корней квадратного уравнения от его коэффициентов и сформулировал свою знаменитую теорему.
Слайд 14Франсуа Виет родился в 1540 г. во Франции, в Фонтене- ле
- Конт. По образованию юрист. Он много занимался адвокатской деятельностью, а с 1571г. по 1584г. был советником короля Георга III и Георга IV. Но все свободное время, весь свой досуг он отдавал занятиям математикой. Особенно усиленно он начал работать в области математики с 1584 г., после отстранения от должности при королевском дворе. Виет детально изучил труды как древних, так и современных ему математиков и создал по существу новую алгебру. Он ввел в нее буквенную символику. После открытия Виета, стало возможным записывать правила в виде формул.
Франсуа Виет
Слайд 15Именно с 1591 г. мы пользуемся формулами при решении квадратных уравнений.
Решим квадратное уравнение х2 + 10х - 39 = 0 современными способами.
Ответ: 3,-13
Слайд 16Следует отметить, что второй коэффициент в данном уравнении четный, что позволяет
использовать иную формулу для решения данного уравнения. х2+10х-39 = 0,
Ответ: 3,-13
Слайд 18Существуют ли другие способы решения квадратных уравнений?
Квадратные уравнения можно решить, используя
свойства «суммы коэффициентов».
Если а + b + с = 0, то x1=1,x2=c ∕ a, = 1;
или если а – b - с = 0,
То x1=-1,x2=-c ∕ a.
Но данное квадратное уравнение нельзя решить, используя эти соотношения. Например, изменим в рассмотренном уравнении свободный член:
Если а + b + с = 0, то x1=1,x2=c ∕ a, = 1;
или если а – b - с = 0,
То x1=-1,x2=-c ∕ a.
Но данное квадратное уравнение нельзя решить, используя эти соотношения. Например, изменим в рассмотренном уравнении свободный член:
Слайд 20В учебнике мы встречаем задания, где четко обозначено, как решить квадратное
уравнение. В предложенных вам задачах вы не только решите уравнение, но и узнаете интересные факты.
Слайд 21Известно, что учет населения проводился в Египте и Китае еще до
нашей эры.
Решив квадратное уравнение 4а2- 24а + 39 = 0, вы определите, в каком это было тысячелетии до н. э.
Решив квадратное уравнение 4а2- 24а + 39 = 0, вы определите, в каком это было тысячелетии до н. э.
Слайд 22На основе статистических данных можно выделить регионы с максимальным сбросом загрязненных
вод: это Краснодарский край и Москва. Сколько процентов общего количества загрязненных вод дают эти регионы, вы узнаете, решив уравнение х2 - 19х + 88 =0.
Слайд 233. Кислотные осадки разрушают сооружения из мрамора и других материалов. Исторические
памятники Греции и Рима, простояв тысячелетия, за последние годы разрушаются прямо на глазах. «Мировой рекорд» принадлежит одному шотландскому городку, где 10 апреля 1974 года выпал дождь, скорее напоминающий столовый уксус, чем воду. Устно решите уравнения, найдите верный ответ и соответствующую ему букву и прочитайте название этого «знаменитого» городка. ( Питлохри)