преподаватель: Ауэлбекова Г.У.
- Главная
- Разное
- Образование
- Спорт
- Естествознание
- Природоведение
- Религиоведение
- Французский язык
- Черчение
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, фоны, картинки для презентаций
- Экология
- Экономика
Презентация, доклад на тему Различные способы решения квадратных уравнении
Содержание
- 1. Различные способы решения квадратных уравнении
- 2. Актуальность проблемыТеория уравнений занимает ведущее место в
- 3. Цель и задачиЦельЗадачивыявить способы решения квадратных уравнений,
- 4. Объект исследования:Предмет исследования:квадратные уравнения.способы решения квадратных уравнений.
- 5. Способы решения квадратных уравненийРазложение левой части на
- 6. По свойствам коэффициентовСвойства:
- 7. Способом «переброски» Умножив обе части уравнения на
- 8. С помощью циркуля и линейкиДанный способ заключается
- 9. С помощью номограммыЭто старый и незаслуженно забытый
- 10. Геометрический способРассмотрим, как древние греки решали уравнениеРешение
- 11. Разложение левой части уравнения на множителиОбработка данныхОтвет: -4,5; 1.Метод выделения полного квадрата
- 12. Обработка данныхОтвет: -4,5; 1.По формулеС использованием формул
- 13. Обработка данныхОтвет: -4,5; 1. Способом «переброски» По
- 14. Обработка данныхОтвет: -4,5; 1.Графический методС помощью циркуля
- 15. Обработка данныхОтвет: -4,5; 1.С помощью номограммыГеометрический способПредставим
- 16. Одни квадратные уравнения можно решить разными способами,
- 17. положительные стороны и недостатки
- 18. Плужников И.10 способов решения квадратных уравнений//Математика в
Слайд 1 МИНИСТЕРСТВА НАУКИ И ОБРАЗОВАНИЯ РЕСПУБЛИКИ КАЗАХСТАН ЛИЦЕЙ ПРИ КАЗГАСА РАЗЛИЧНЫЕ СПОСОБЫ РЕШЕНИЯ КВАДРАТНЫХ
Слайд 2Актуальность проблемы
Теория уравнений занимает ведущее место в алгебре и математике в
Слайд 3Цель и задачи
Цель
Задачи
выявить способы решения квадратных уравнений, узнать можно ли решить
проанализировать источники литературы для выявления способов решения квадратных уравнений, показать различные способы
решения квадратных уравнений.
Слайд 4Объект исследования:
Предмет исследования:
квадратные уравнения.
способы решения
квадратных уравнений.
Слайд 5
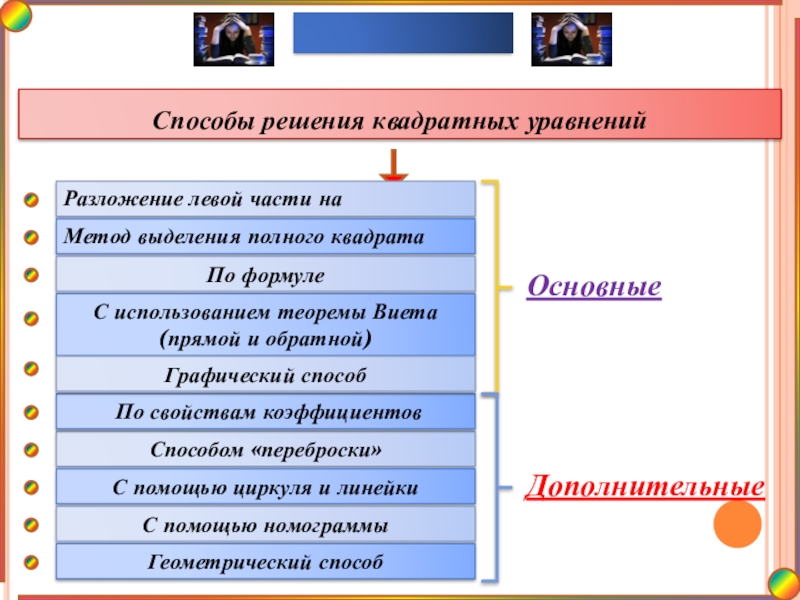
Способы решения квадратных уравнений
Разложение левой части на множители
Метод выделения полного квадрата
По
С использованием теоремы Виета (прямой и обратной)
Способом «переброски»
По свойствам коэффициентов
Графический способ
С помощью циркуля и линейки
С помощью номограммы
Геометрический способ
Основные
Дополнительные
Слайд 7
Способом «переброски»
Умножив обе части уравнения на а, получим
Пусть
, откуда
Тогда получим уравнение с новой переменной
Его корни у1 и у2. Окончательно
Слайд 8
С помощью циркуля и линейки
Данный способ заключается в том, чтобы при
отметить в системе координат точки
и А(0;1); провести окружность с центром в точке S и радиусом SA. Абсциссы точек пересечения с осью Ох есть корни исходного уравнения
Слайд 9
С помощью номограммы
Это старый и незаслуженно забытый способ решения квадратных уравнений.
Для этого надо на оси р взять точку M с координатой р, на оси q – точку N с координатой q и провести прямую MN. Каждая точка пересечения прямой MN с кривой Г даѐт положительный корень уравнения.
Построенная прямая MN может пересекаться с кривой Г:
в двух точках (в этом случае оба корня данного уравнения положительны);
в одной точке (в этом случае второй корень уравнения отрицателен);
может касаться кривой (в этом случае у уравнения кратный положительный корень);
может не иметь с кривой Г ни одной общей точки (в этом случае либо оба корня уравнения отрицательны, либо у него вообще нет действительных корней).
Слайд 10
Геометрический способ
Рассмотрим, как древние греки решали уравнение
Решение представлено на рисунке, где
Выражения
геометрически представляют собой один и тот же квадрат со стороной 5. Поэтому
или
и 16 + 9
Слайд 11
Разложение левой части
уравнения на множители
Обработка данных
Ответ: -4,5; 1.
Метод выделения
полного
Слайд 12
Обработка данных
Ответ: -4,5; 1.
По формуле
С использованием
формул Виета
имеет два разных
больший по модулю
корень отрицательный
Слайд 13
Обработка данных
Ответ: -4,5; 1.
Способом «переброски»
По свойству коэффициентов
Перебросим коэффициент а
из которого по формулам Виета
Корнями исходного уравнения будут
Так как
то
Слайд 14
Обработка данных
Ответ: -4,5; 1.
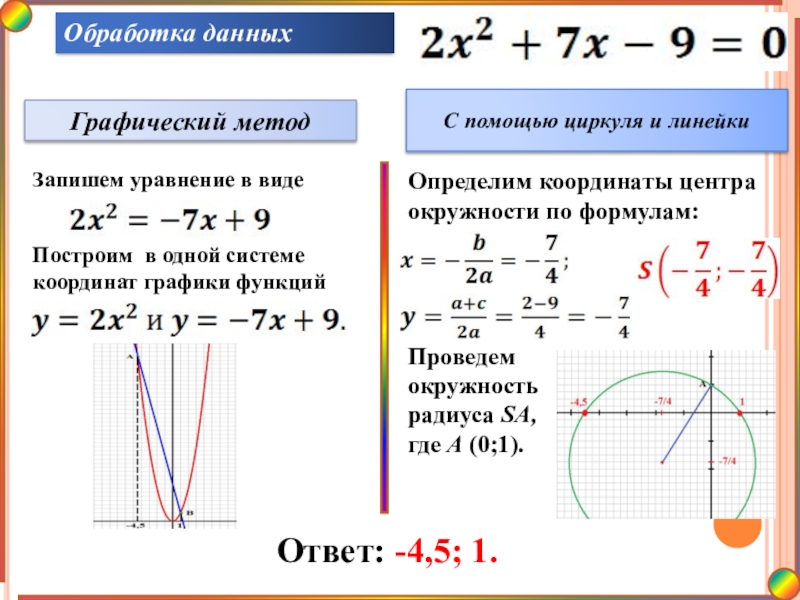
Графический метод
С помощью циркуля и линейки
Запишем уравнение в
Построим в одной системе координат графики функций
Определим координаты центра окружности по формулам:
Проведем окружность радиуса SA, где А (0;1).
Слайд 15
Обработка данных
Ответ: -4,5; 1.
С помощью номограммы
Геометрический способ
Представим уравнение в виде:
Номограмма дает
отрицательный корень
Представим уравнение в виде:
Площадь полученного квадрата:
Так как
, то:
Таким образом, получили уравнение:
Слайд 16Одни квадратные уравнения можно решить разными способами, а для других уравнений
Анализ данных
Основным в решении квадратных уравнений является правильно выбрать рациональный способ решения и применить алгоритм решения
Данные способы решения заслуживают внимания, поскольку они не все отражены в школьных учебниках математики. Овладение данными способами поможет учащимся экономить время и эффективно решать уравнения, так как потребность в быстром решении обусловлена применением тестовой системы вступительных экзаменов.
Слайд 18Плужников И.10 способов решения квадратных уравнений//Математика в школе.-2000.-№40
Гусев В. А., Мордкович
Глейзер Г. И. История математики в школе. – М.: просвещение, 1982
Брадис В. М. Четырехзначные математические таблицы для средней школы. – м., просвещение, 1990
Дидактические материалы по алгебре.
http://revolution.allbest.ru/
http://mat.1september.ru/2001/42/no42_01.htm
Список использованной литературы