Презентация
учителя математики
МБОУ «СШ №8»
г. Архангельска
Докуниной Марины Сергеевны
- Главная
- Разное
- Образование
- Спорт
- Естествознание
- Природоведение
- Религиоведение
- Французский язык
- Черчение
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, фоны, картинки для презентаций
- Экология
- Экономика
Презентация, доклад на тему Рациональные уравнения как математические модели реальных ситуаций
Содержание
- 1. Рациональные уравнения как математические модели реальных ситуаций
- 2. Тема урока«Рациональные уравнения как математические модели реальных ситуаций»
- 3. Цель урокаСформировать алгоритм решения текстовых задач помощью
- 4. Уравнения вида r(x)=0 называют рациональным, если r(x)-
- 5. В
- 6. Решим уравнение x2+10x=39
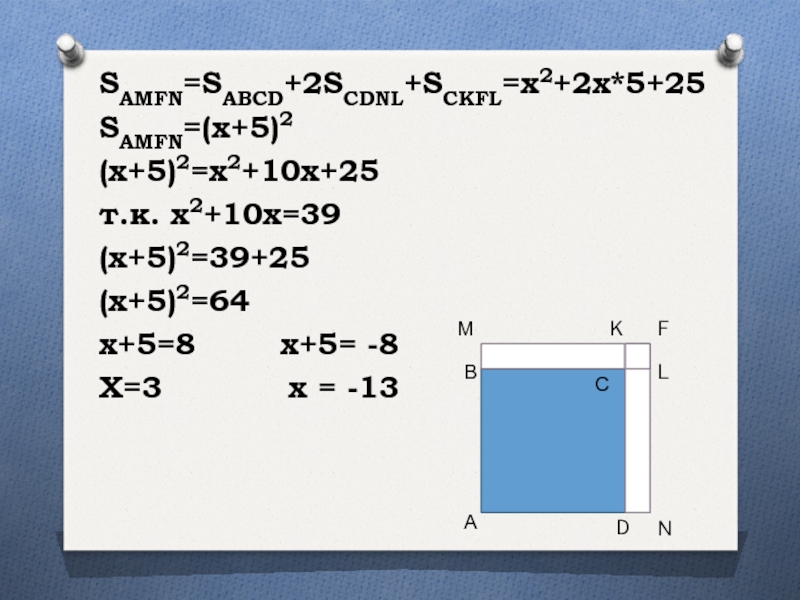
- 7. SAMFN=SABCD+2SCDNL+SCKFL=x2+2x*5+25SAMFN=(x+5)2(x+5)2=x2+10x+25т.к. x2+10x=39(x+5)2=39+25(x+5)2=64х+5=8 х+5= -8Х=3 х = -13АВСDМFNKL
- 8. Решение квадратных уравнений по формуле.
- 9. Решение квадратного уравнения по формуле
- 10. Реши уравнения и выбери правильный ответ
- 11. Ответы
- 12. Этапы решения задачи:1) Проанализируем текст задачи и
- 13. № 1
- 14. Из города А в город В, расстояние
- 15. РешениеПусть х км/ч – скорость второго велосипедистаИзвестно,
- 16. Решение
- 17. Реши самостоятельно
- 18. Из пунктов А и В навстречу друг
- 19. РешениеПо условию задачи время движения первого пешехода на 1 ч меньше времени движения второго.АВ
- 20. РешениеСоставим и решим уравнение:Число -5 противоречит смыслу
- 21. № 2
- 22. Катер, собственная скорость которого 8 км/ч, прошёл
- 23. РешениеИзвестно, что время, затраченное на весь путь, равно 4 ч.Пусть х км/ч – скорость течения реки.
- 24. РешениеСоставим и решим уравнение:Число -2 противоречит смыслу
- 25. Реши самостоятельно
- 26. Расстояние между пристанями по реке равно 21
- 27. РешениеПо условию задачи время, затраченное моторной лодкой
- 28. РешениеСоставим и решим уравнение:Число
- 29. --Я
- 30. Слайд 30
Тема урока«Рациональные уравнения как математические модели реальных ситуаций»
Слайд 3Цель урока
Сформировать алгоритм решения текстовых задач помощью рациональных уравнений, сводимых к
квадратным;
Закрепить навык решения квадратных уравнений с помощью формул
Закрепить навык решения квадратных уравнений с помощью формул
Слайд 4Уравнения вида r(x)=0 называют рациональным, если r(x)- алгебраическое уравнение, составленное из
чисел и переменной x с помощью операций сложения, вычитания, умножения, деления и возведения в степень.
Уравнения вида ax2+bx+c=0, где a≠0
называют квадратным уравнением.
Если а=1, то уравнение называют
приведенным квадратным уравнением.
Уравнения вида ax2+bx+c=0, где a≠0
называют квадратным уравнением.
Если а=1, то уравнение называют
приведенным квадратным уравнением.
Слайд 5
В Греции математики овладели искусством
решать квадратные уравнения путем использования геометрической алгебры.
Примеры геометрического решения квадратных уравнений приводятся в знаменитой «Алгебре Мухаммеда аль-Хорезми»
Примеры геометрического решения квадратных уравнений приводятся в знаменитой «Алгебре Мухаммеда аль-Хорезми»
Слайд 6Решим уравнение x2+10x=39
Построим квадрат ABCD со
стороной
х см и на его сторонах ВС и СD равные прямоугольники с высотой 5 см.
M K F
В С L
А D N
х см и на его сторонах ВС и СD равные прямоугольники с высотой 5 см.
M K F
В С L
А D N
Слайд 7SAMFN=SABCD+2SCDNL+SCKFL=x2+2x*5+25
SAMFN=(x+5)2
(x+5)2=x2+10x+25
т.к. x2+10x=39
(x+5)2=39+25
(x+5)2=64
х+5=8 х+5= -8
Х=3
х = -13
А
В
С
D
М
F
N
K
L
Слайд 12Этапы решения задачи:
1) Проанализируем текст задачи и составим ее модель (таблицу)
2) Работа с составленной моделью (решение рационального уравнения)
3)Проанализировать и выбрать ответ, соответствующий тексту задачи.
3)Проанализировать и выбрать ответ, соответствующий тексту задачи.
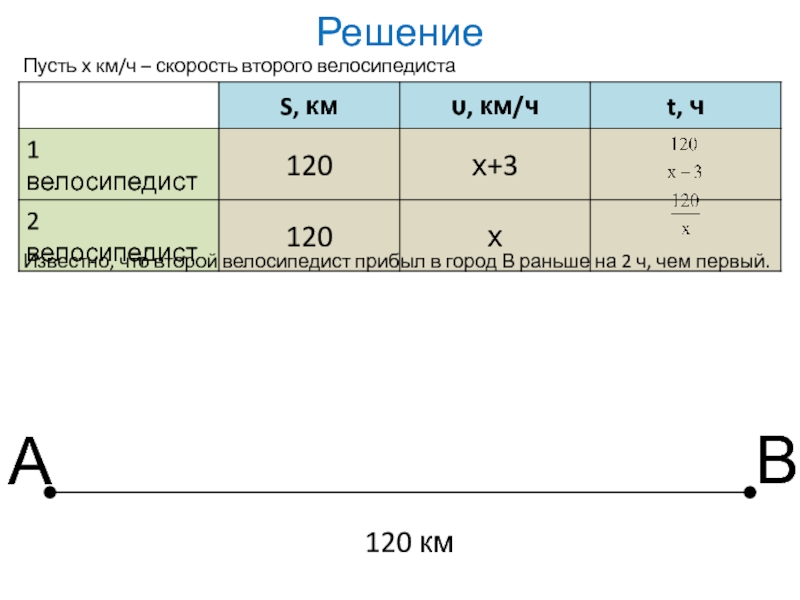
Слайд 14Из города А в город В, расстояние между которыми 120 км,
выехали одновременно два велосипедиста. Скорость первого на 3 км/ч больше скорости второго, поэтому он прибыл в город В на 2 ч раньше. Определите скорость велосипедистов.
Условие
А
В
120 км
Слайд 15Решение
Пусть х км/ч – скорость второго велосипедиста
Известно, что второй велосипедист прибыл
в город В раньше на 2 ч, чем первый.
А
В
120 км
Слайд 16Решение
Составим и решим уравнение:
Умножим обе части этого уравнения на x(x+3)
Ответ: 12 км/ч; 15 км/ч.
Число -15 противоречит смыслу задачи
Если х=12, то х(х+3)≠0, верно
12 км/ч – скорость второго велосипедиста
15 км/ч – скорость первого велосипедиста
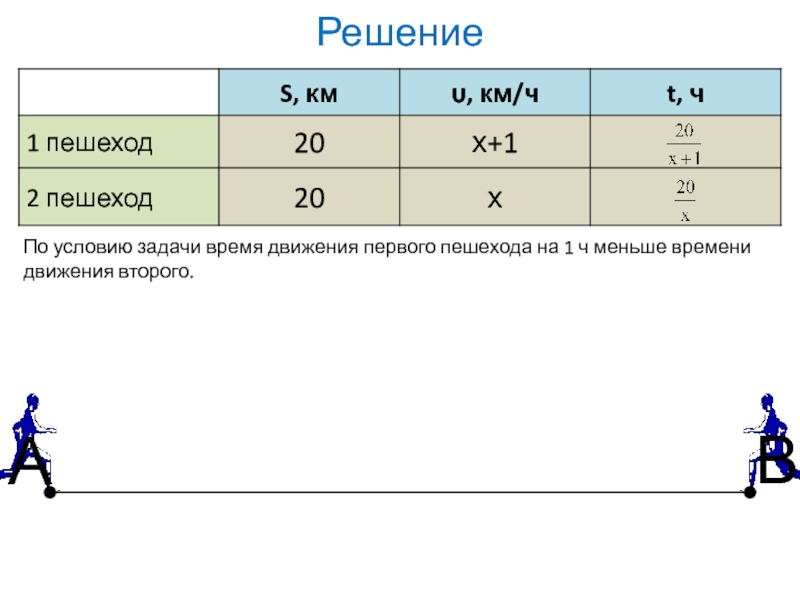
Слайд 18Из пунктов А и В навстречу друг другу одновременно вышли два
пешехода. Скорость первого на 1 км/ч больше скорости второго, поэтому он прибыл в пункт В на 1 ч раньше, чем второй в пункт А. Найдите скорости пешеходов, если расстояние между пунктами А и В равно 20 км.
Условие
А
В
Слайд 19Решение
По условию задачи время движения первого пешехода на 1 ч меньше
времени движения второго.
А
В
Слайд 20Решение
Составим и решим уравнение:
Число -5 противоречит смыслу задачи
Если х=4, то х(х+1)≠0,
верно
4 км/ч – скорость второго пешехода
5 км/ч – скорость первого пешехода
4 км/ч – скорость второго пешехода
5 км/ч – скорость первого пешехода
Ответ: 5 км/ч; 4 км/ч.
Слайд 22Катер, собственная скорость которого 8 км/ч, прошёл по реке расстояние, равное
15 км, по течению и такое же расстояние против течения. Найдите скорость течения реки, если время, затраченное на весь путь, равно 4 ч.
Условие
Слайд 23Решение
Известно, что время, затраченное на весь путь, равно 4 ч.
Пусть х
км/ч – скорость течения реки.
Слайд 24Решение
Составим и решим уравнение:
Число -2 противоречит смыслу задачи
Если х=2, то (8-х)(8+х)≠0,
верно
2 км/ч – скорость течения реки
2 км/ч – скорость течения реки
Ответ: 2 км/ч.
Слайд 26Расстояние между пристанями по реке равно 21 км. Моторная лодка отправилась
от одной к другой и через 4 ч вернулась назад, затратив 24 мин. на стоянку. Найти собственную скорость лодки, если скорость течения реки равна 2 км/ч.
Условие
Слайд 27Решение
По условию задачи время, затраченное моторной лодкой на весь путь по
реке, равно
Пусть х км/ч – собственная скорость моторной лодки.
Слайд 28Решение
Составим и решим уравнение:
Число противоречит смыслу задачи
Если
х=12, то (х-2)(х+2)≠0, верно
12 км/ч – собственная скорость моторной лодки
12 км/ч – собственная скорость моторной лодки
Ответ: 12 км/ч.
Слайд 29 --Я хорошо понял (а) тему
и домашнее
задание смогу выполнить без труда.
- Я плохо понял (а) тему и буду
затрудняться при выполнении
домашнего задания.
- Я ничего не понял (а) и не смогу выполнить домашнее задание.
задание смогу выполнить без труда.
- Я плохо понял (а) тему и буду
затрудняться при выполнении
домашнего задания.
- Я ничего не понял (а) и не смогу выполнить домашнее задание.
