- Главная
- Разное
- Образование
- Спорт
- Естествознание
- Природоведение
- Религиоведение
- Французский язык
- Черчение
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, фоны, картинки для презентаций
- Экология
- Экономика
Презентация, доклад на тему Рациональные и иррациональные числа.
Содержание
- 1. Рациональные и иррациональные числа.
- 2. ПовторениеЧисла 1, 2, 3 … - натуральные
- 3. ПовторениеМножество целых чисел =натуральные числа + противоположные
- 4. ПовторениеДробные числа
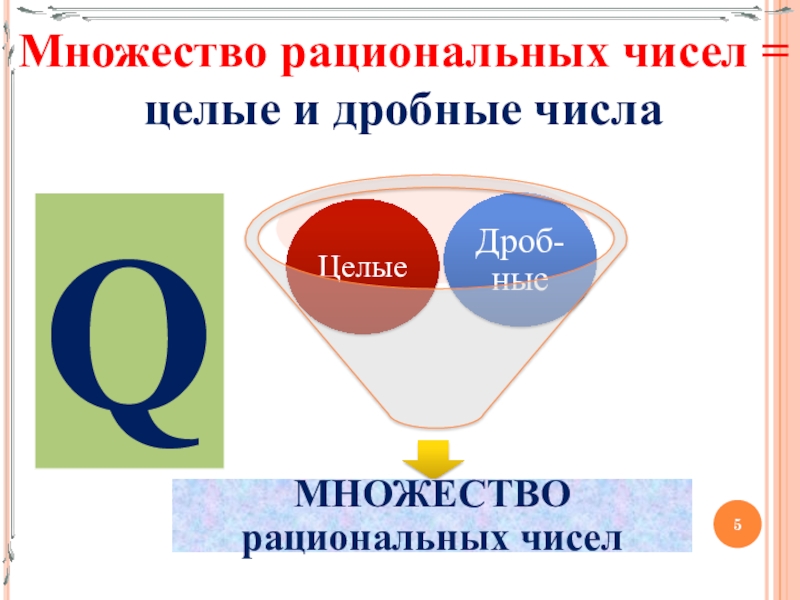
- 5. Множество рациональных чисел =целые и дробные числаQ
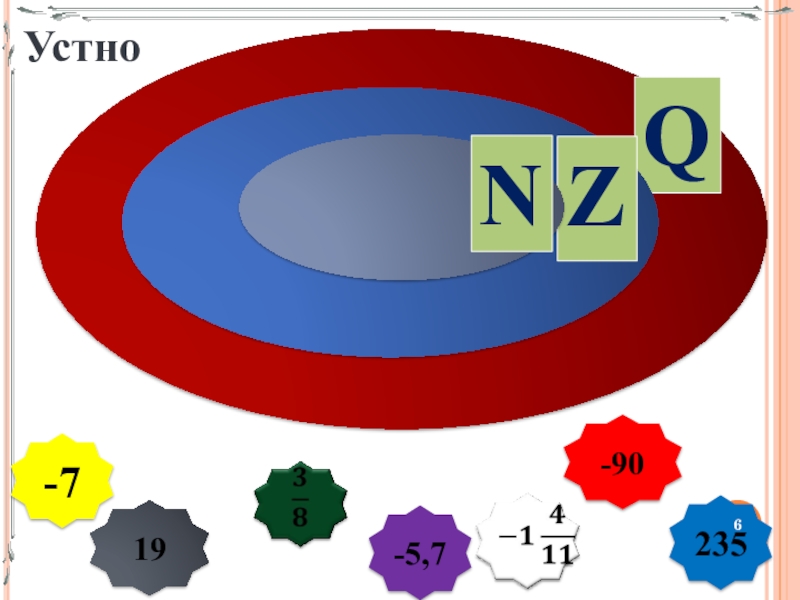
- 6. 235-719-5,7Устно-90
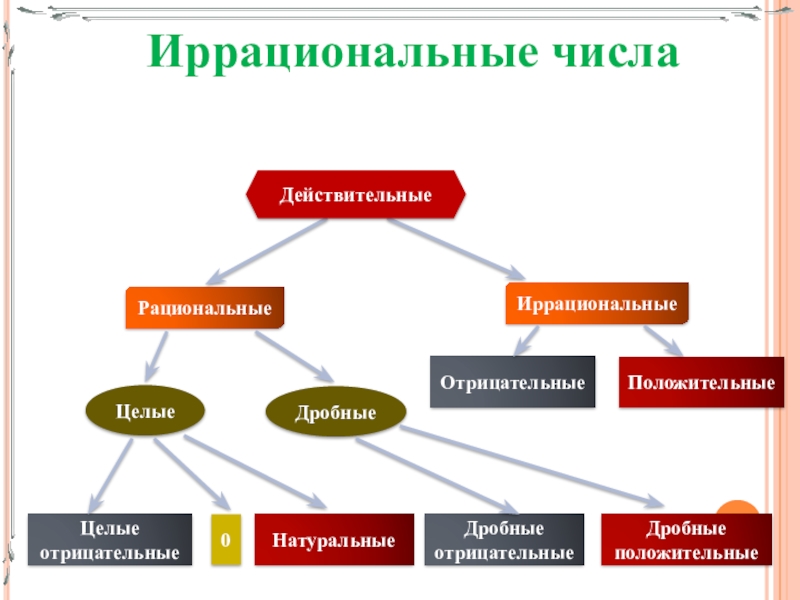
- 7. Иррациональные числаЦелые отрицательные0НатуральныеДробные отрицательныеДробные положительныеЦелыеДробныеРациональныеИррациональныеОтрицательныеПоложительныеДействительные
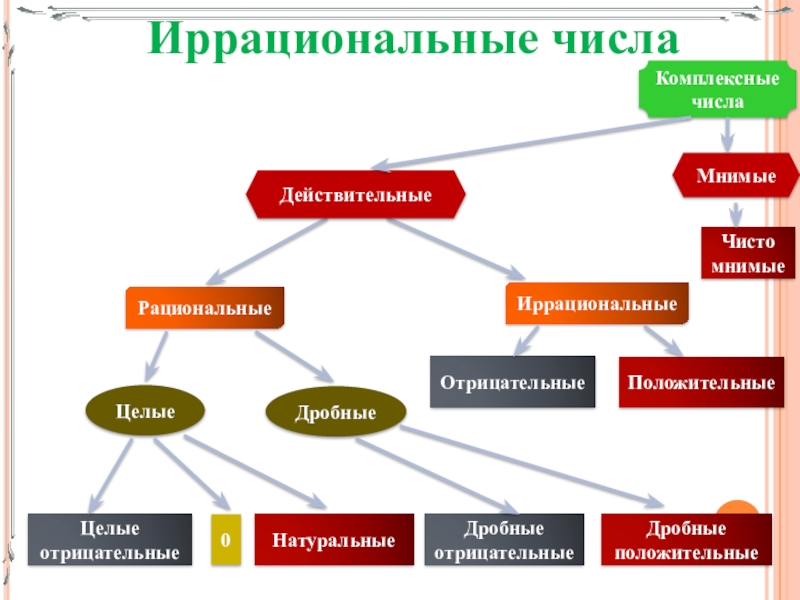
- 8. Иррациональные числа
- 9. ИсторияМатематики Древней Греции более двадцати веков тому
- 10. Измерение длин отрезков на координатной прямойРабота
- 11. Среди рациональных чисел нет такого числа, квадрат которого равен 2.
- 12. Число
- 13. Слайд 13
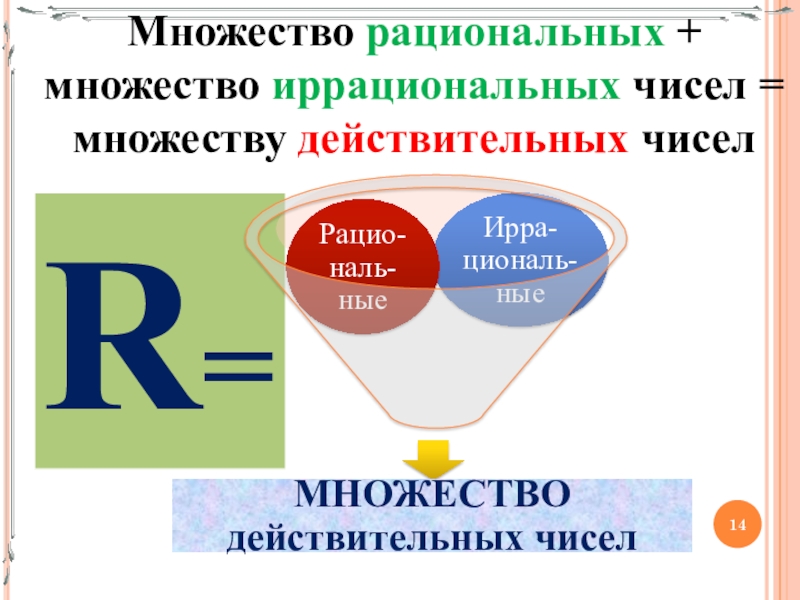
- 14. Множество рациональных + множество иррациональных чисел = множеству действительных чиселR=
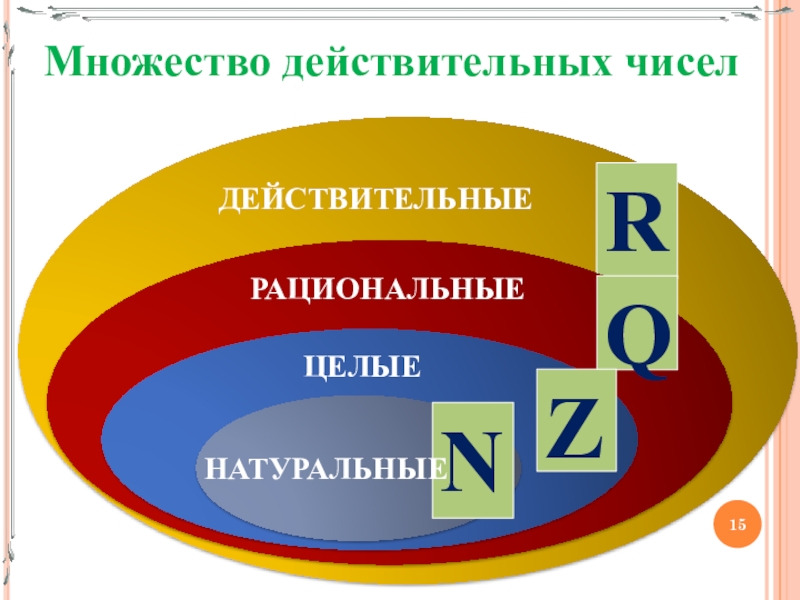
- 15. НАТУРАЛЬНЫЕЦЕЛЫЕРАЦИОНАЛЬНЫЕДЕЙСТВИТЕЛЬНЫЕМножество действительных чисел
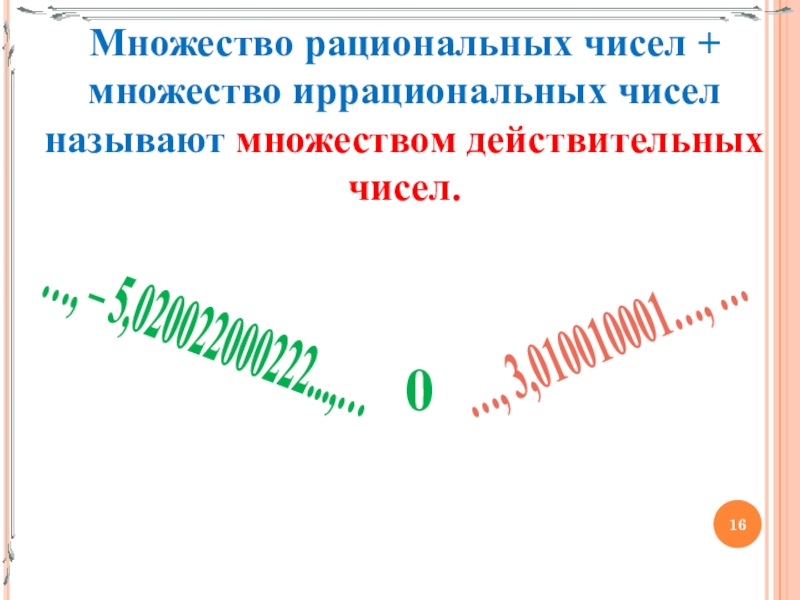
- 16. Множество рациональных чисел + множество иррациональных чисел называют множеством действительных чисел.…, 3,010010001…, …0…, – 5,020022000222...,…
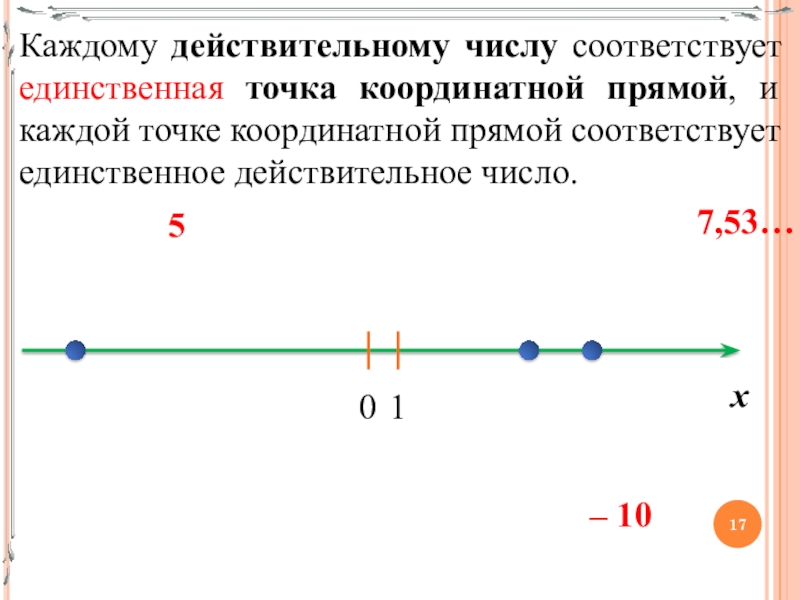
- 17. Каждому действительному числу соответствует единственная точка координатной
- 18. Между множеством действительных чисел и множеством точек координатной прямой существует взаимно однозначное соответствие.
- 19. Сравнение иррациональных чиселСравним числа 2,36366… и 2,37011…
- 20. Слайд 20
- 21. КластерИррациональные числаНатуральныечислаЦелые числаРациональныечисла907–6(3)7,020020002…345π1,24(53)
- 22. № 276, № 277, № 279№ 280, № 281 (а, в, д).№ 285, № 286.Упражнения
- 23. Задача на повторениеВ дивизионном полку за 20
- 24. Вопросы– Какие числа называются рациональными?– Какие числа называются иррациональными?– Из каких чисел состоит множество действительных чисел?
- 25. Задание на самоподготовку:№ 278, № 281 (б, г, е), № 282
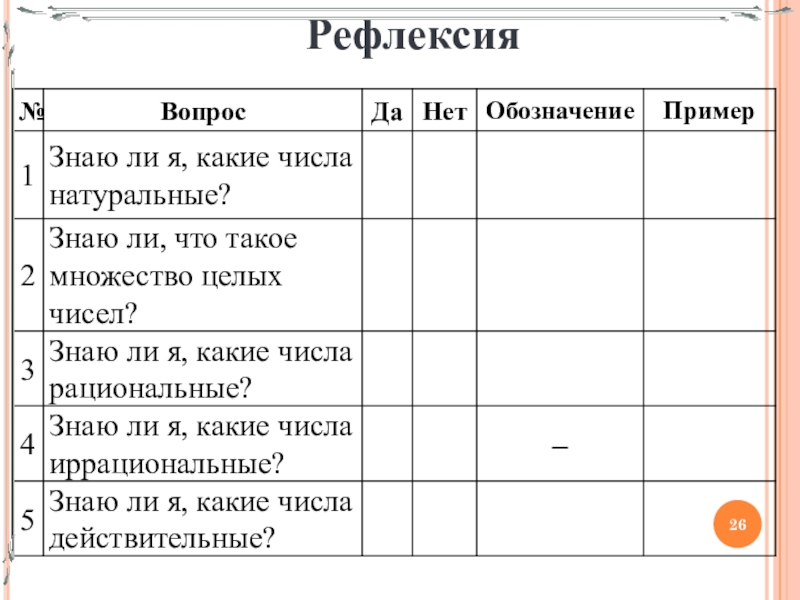
- 26. Рефлексия
ПовторениеЧисла 1, 2, 3 … - натуральные числаНатуральные числа – числа, возникающие естественным образом при счёте.Существуют два подхода к определению натуральных чисел — числа, используемые при:перечислении (нумеровании) предметов (первый, второй, третий, …);обозначении количества предметов (нет предметов, один предмет, два предмета, …).1-й танк2-й танк3-й
Слайд 2Повторение
Числа 1, 2, 3 … - натуральные числа
Натуральные числа – числа, возникающие
естественным образом при счёте.
Существуют два подхода к определению натуральных чисел — числа, используемые при:
перечислении (нумеровании) предметов
(первый, второй, третий, …);
обозначении количества предметов (нет предметов, один предмет, два предмета, …).
Существуют два подхода к определению натуральных чисел — числа, используемые при:
перечислении (нумеровании) предметов
(первый, второй, третий, …);
обозначении количества предметов (нет предметов, один предмет, два предмета, …).
1-й танк
2-й танк
3-й танк
N
Слайд 3Повторение
Множество целых чисел =
натуральные числа + противоположные им числа и нуль
-5,
-4, -3, -2, -1, 0, 1, 2, 3, 4, 5
Z
Слайд 7Иррациональные числа
Целые отрицательные
0
Натуральные
Дробные отрицательные
Дробные положительные
Целые
Дробные
Рациональные
Иррациональные
Отрицательные
Положительные
Действительные
Слайд 9История
Математики Древней Греции более двадцати веков тому назад пришли к выводу,
что нет ни целого, ни дробного числа, выражающего диагональ квадрата со стороной 1. Это вызвало кризис в математической науке: диагональ у квадрата есть, а длины у неё нет!
Математики нашли выход из этой ситуации: раз имеющегося запаса чисел – целых и дробных – не хватает для выражения длин отрезков, значит, нужны какие-то новые числа. Так появились иррациональные числа.
Математики нашли выход из этой ситуации: раз имеющегося запаса чисел – целых и дробных – не хватает для выражения длин отрезков, значит, нужны какие-то новые числа. Так появились иррациональные числа.
Слайд 10Измерение длин отрезков на координатной прямой
Работа с учебником стр.63 –
64
п. 11.
Устно ответить на вопросы:
Как можно измерить длину любого отрезка?
Как можно получить более точный результат (с точностью до 0,1; 0,01 и 0,001?
Какие числа окажутся в результате измерений?
п. 11.
Устно ответить на вопросы:
Как можно измерить длину любого отрезка?
Как можно получить более точный результат (с точностью до 0,1; 0,01 и 0,001?
Какие числа окажутся в результате измерений?
Иррациональные числа
Слайд 16Множество рациональных чисел + множество иррациональных чисел называют множеством действительных чисел.
…,
3,010010001…, …
0
…, – 5,020022000222...,…
Слайд 17Каждому действительному числу соответствует единственная точка координатной прямой, и каждой точке
координатной прямой соответствует единственное действительное число.
х
5
0
1
– 10
7,53…
Слайд 18Между множеством действительных чисел и множеством точек координатной прямой существует взаимно
однозначное соответствие.
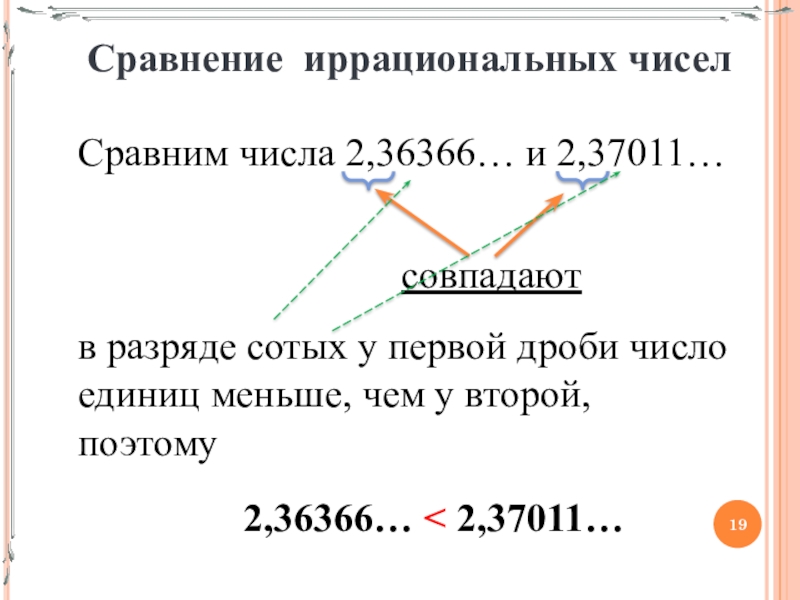
Слайд 19Сравнение иррациональных чисел
Сравним числа 2,36366… и 2,37011…
совпадают
в разряде сотых у
первой дроби число единиц меньше, чем у второй, поэтому
2,36366… < 2,37011…
Слайд 21Кластер
Иррациональные числа
Натуральные
числа
Целые
числа
Рациональные
числа
9
0
7
–6(3)
7,020020002…
345
π
1,24(53)
Слайд 23Задача на повторение
В дивизионном полку за 20 секунд выпускают 120 ракет.
Сколько ракет выпустят за 4 секунды.
Слайд 24Вопросы
– Какие числа называются рациональными?
– Какие числа называются иррациональными?
– Из каких
чисел состоит множество действительных чисел?