- Главная
- Разное
- Образование
- Спорт
- Естествознание
- Природоведение
- Религиоведение
- Французский язык
- Черчение
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, фоны, картинки для презентаций
- Экология
- Экономика
Презентация, доклад на тему Производная и ее применение (10-11 класс)
Содержание
- 1. Производная и ее применение (10-11 класс)
- 2. Причины невыполнения заданий на производную- во-первых, производная
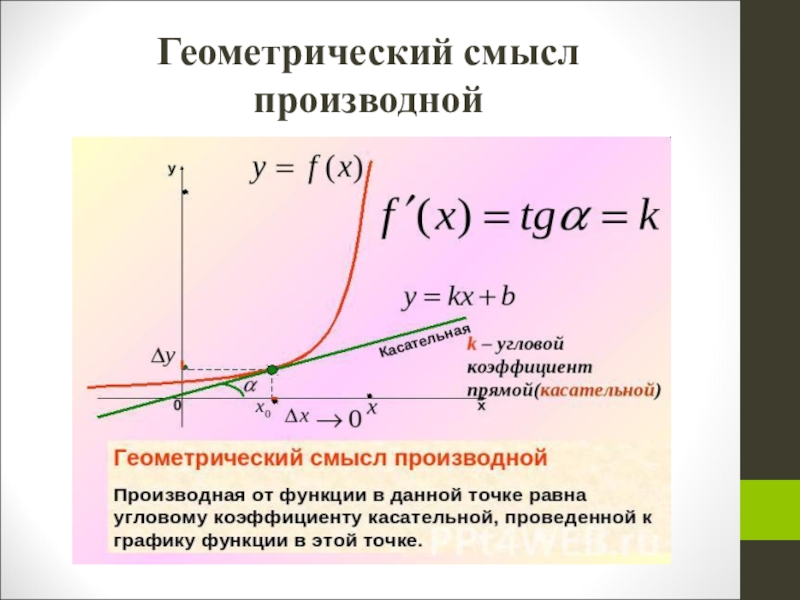
- 3. Геометрический смысл производной
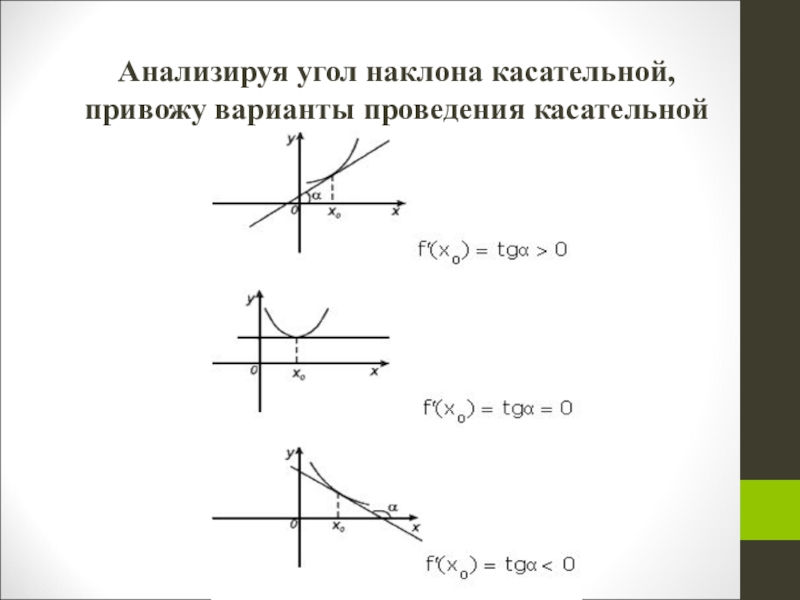
- 4. Анализируя угол наклона касательной, привожу варианты проведения касательной
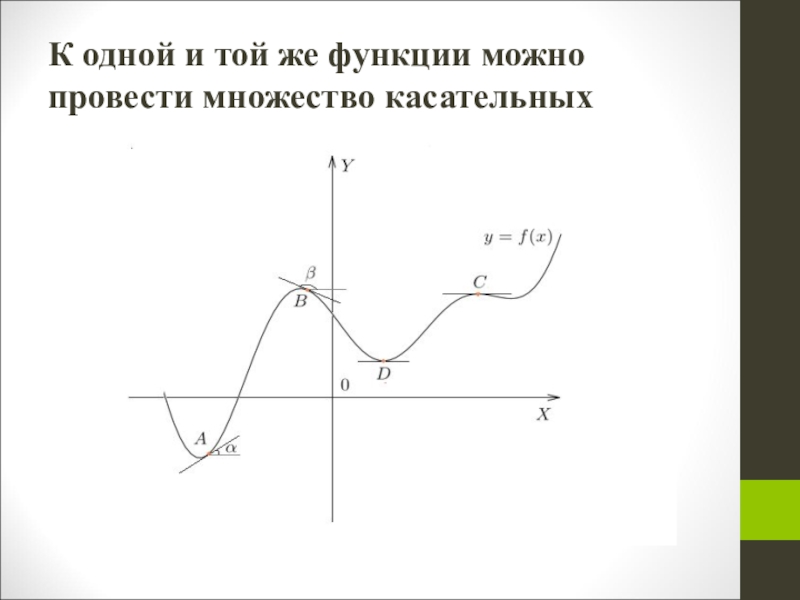
- 5. К одной и той же функции можно провести множество касательных
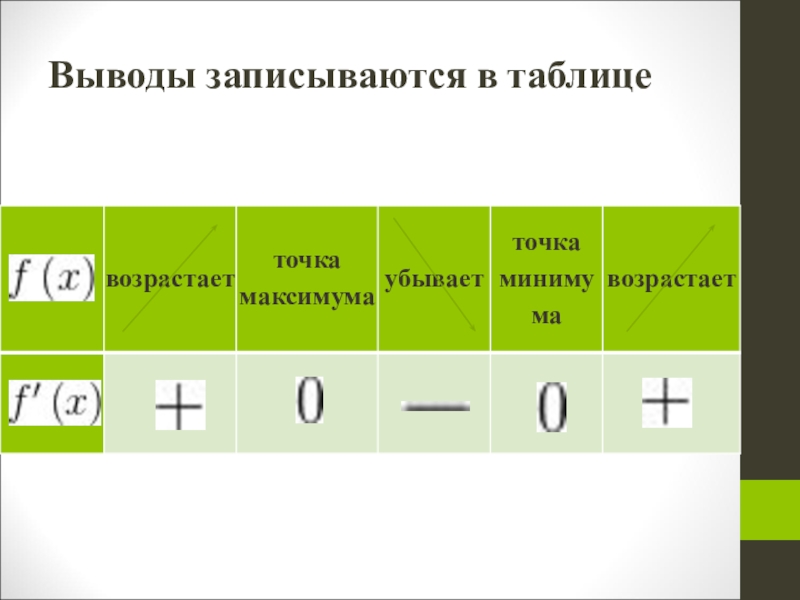
- 6. Выводы записываются в таблице
- 7. Физический смысл производнойпроизводная — это скорость изменения функции
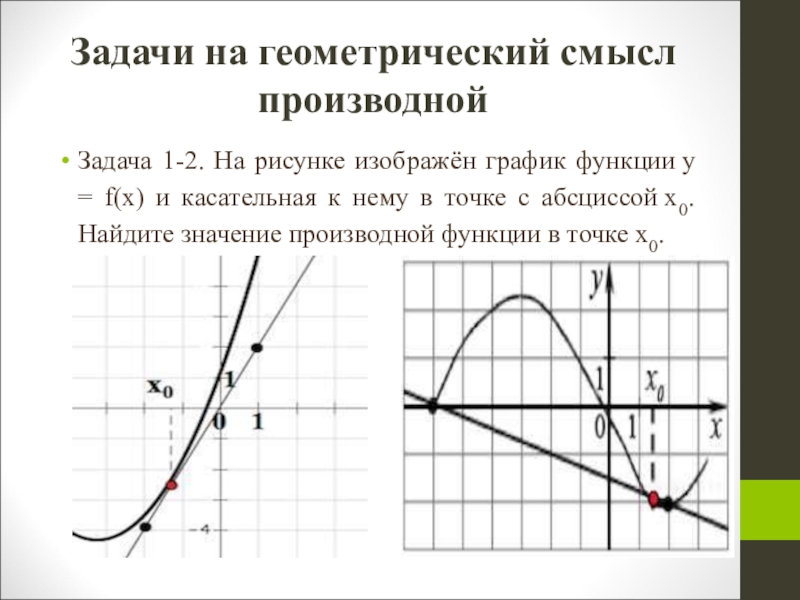
- 8. Задачи на геометрический смысл производнойЗадача 1-2. На
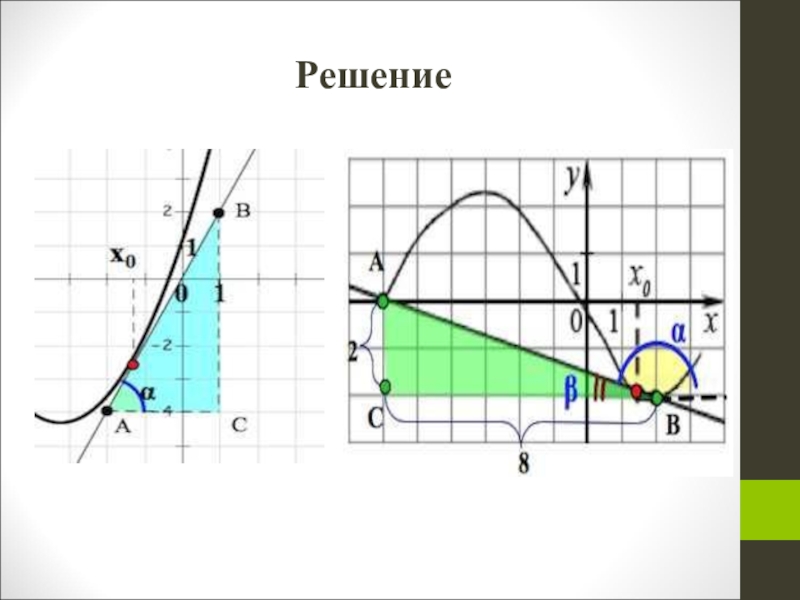
- 9. Решение
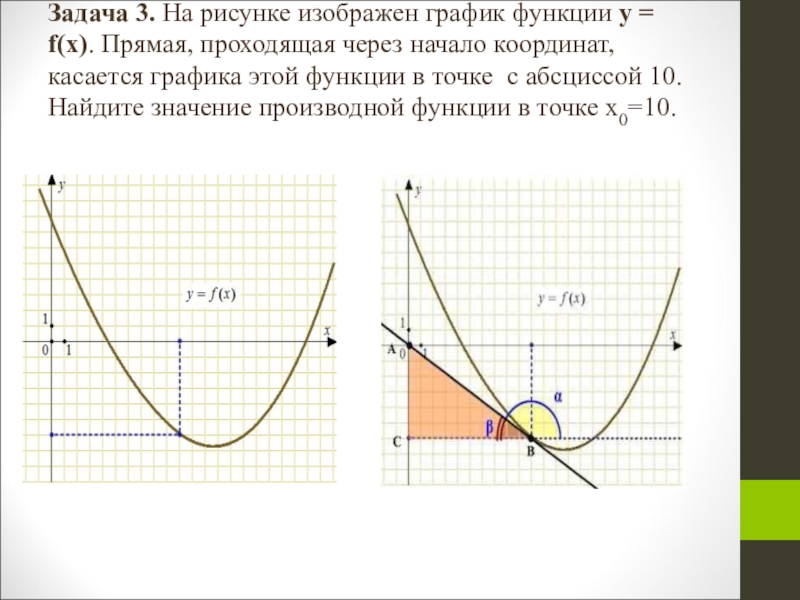
- 10. Задача 3. На рисунке изображен график функции у
- 11. Задача 4. Прямая y = 5x −
- 12. Задачи на физический смысл производнойЗадача 1Материальная точка
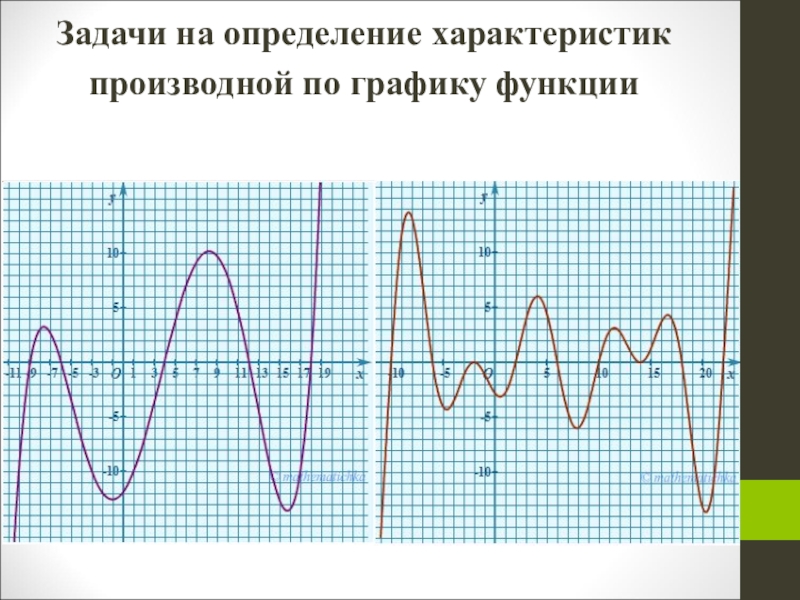
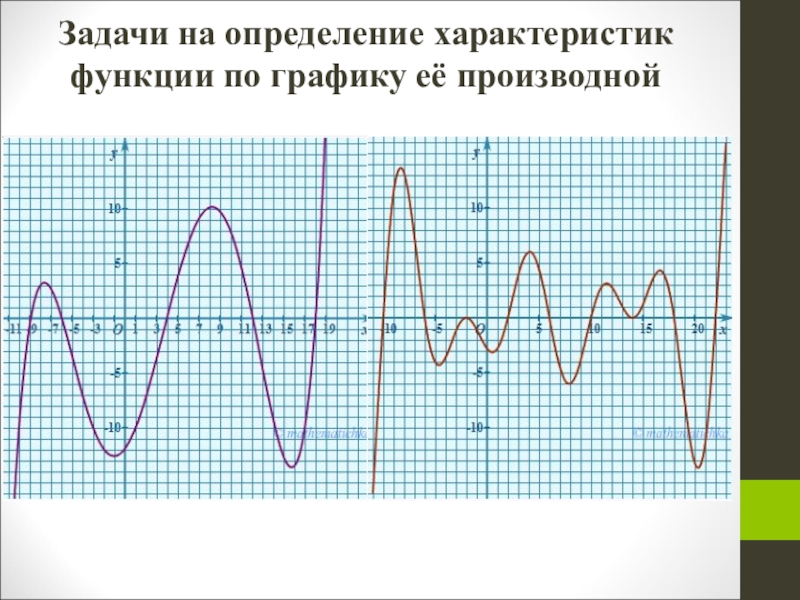
- 13. Задачи на определение характеристик производной по графику функции
- 14. Задачи на определение характеристик функции по графику её производной
- 15. Слайд 15
- 16. Задачи на нахождение точек экстремума функцииАлгоритм нахождения
- 17. Задачи на нахождение экстремумов функции 1) Находим
- 18. Задачи на определение наибольшего (наименьшего) значения функции
- 19. Утверждения, полезные для отыскания наибольшего или
Причины невыполнения заданий на производную- во-первых, производная - материал курса алгебры и начал 10-11 классов, для освоения которого необходима достаточная база знаний программы основной школы;- во-вторых, несмотря на невысокий уровень сложности самого задания, спектр проверки понимания
Слайд 2Причины невыполнения заданий на производную
- во-первых, производная - материал курса алгебры
и начал 10-11 классов, для освоения которого необходима достаточная база знаний программы основной школы;
- во-вторых, несмотря на невысокий уровень сложности самого задания, спектр проверки понимания темы «производная» в этом задании довольно широк – предлагаются и задачи на геометрический и физический смысл производной, и задачи с множеством ситуаций, описывающих связь между поведением функции и ее производной;
- в-третьих, для решения большинства задач на производную требуется не просто непосредственно применить алгоритм, а самостоятельно проанализировать ситуацию и сделать вывод.
- во-вторых, несмотря на невысокий уровень сложности самого задания, спектр проверки понимания темы «производная» в этом задании довольно широк – предлагаются и задачи на геометрический и физический смысл производной, и задачи с множеством ситуаций, описывающих связь между поведением функции и ее производной;
- в-третьих, для решения большинства задач на производную требуется не просто непосредственно применить алгоритм, а самостоятельно проанализировать ситуацию и сделать вывод.
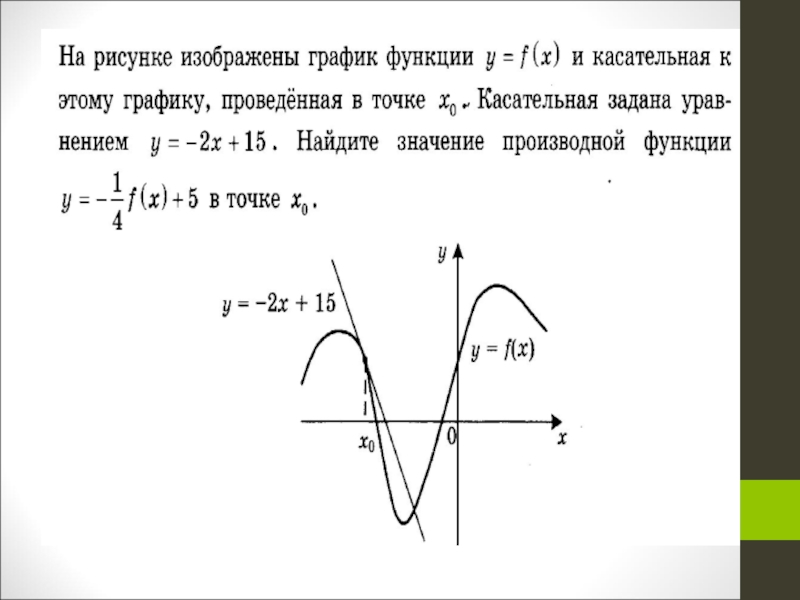
Слайд 8Задачи на геометрический смысл производной
Задача 1-2. На рисунке изображён график функции у
= f(x) и касательная к нему в точке с абсциссой x0. Найдите значение производной функции в точке x0.
Слайд 10Задача 3. На рисунке изображен график функции у = f(x). Прямая, проходящая
через начало координат, касается графика этой функции в точке с абсциссой 10. Найдите значение производной функции в точке x0=10.
Слайд 11 Задача 4. Прямая y = 5x − 3 параллельна касательной к графику функции y = x2 + 2x −
4. Найдите абсциссу точки касания.
Задача 5.
Прямая y = 3x + 1 является касательной к графику функции ax2 + 2x + 3. Найдите a.
Задача 6.
Прямая y = −5x + 8 является касательной к графику функции 28x2 + bx +15. Найдите b, учитывая, что абсцисса точки касания больше 0.
Задача 7.
Прямая y = 3x + 4 является касательной к графику функции 3x2 − 3x + c. Найдите c.
f/(x0)=k,
{ kx0+b=f(x0)
Слайд 12Задачи на физический смысл производной
Задача 1
Материальная точка движется прямолинейно по закону x(t)
= 6t2 − 48t + 17, где x - расстояние от точки отсчета в метрах, t - время в секундах, измеренное с начала движения. Найдите ее скорость (в метрах в секунду) в момент времени t = 9с.
Задача 2
Материальная точка движется прямолинейно по закону x(t) = t2 − 13t + 23, где x - расстояние от точки отсчета в метрах, t - время в секундах, измеренное с начала движения. В какой момент времени (в секундах) ее скорость была равна 3 м/с?
Задача 2
Материальная точка движется прямолинейно по закону x(t) = t2 − 13t + 23, где x - расстояние от точки отсчета в метрах, t - время в секундах, измеренное с начала движения. В какой момент времени (в секундах) ее скорость была равна 3 м/с?
Слайд 16Задачи на нахождение точек экстремума функции
Алгоритм нахождения точек экстремума
Найти область определения
функции.
Найти её производную f'(x).
Найти точки, в которых f'(x) не существует.
Найти точки, в которых f'(x) = 0.
Отметить на числовой прямой область определения функции и все точки, выявленные в п.3 и п.4 (критические точки). Получатся промежутки области определения, на которых производная сохраняет постоянный знак.
Определить знак f'(x) для каждого промежутка.
Определить по знакам производной участки возрастания и убывания функции и сделать выводы о наличии или отсутствии экстремума и его характере в каждой из критических точек.
Найти её производную f'(x).
Найти точки, в которых f'(x) не существует.
Найти точки, в которых f'(x) = 0.
Отметить на числовой прямой область определения функции и все точки, выявленные в п.3 и п.4 (критические точки). Получатся промежутки области определения, на которых производная сохраняет постоянный знак.
Определить знак f'(x) для каждого промежутка.
Определить по знакам производной участки возрастания и убывания функции и сделать выводы о наличии или отсутствии экстремума и его характере в каждой из критических точек.
Слайд 17Задачи на нахождение экстремумов функции
1) Находим точки экстремумов функции и определяем
их характер так же, как в задачах выше.
2) Определяем значения функции в точках максимума или минимума в соответствии с вопросом задачи.
3) Если точек максимума (минимума) на области определения функции несколько, то максимумы (минимумы) называются локальными, а самый большой (самый маленький) называется глобальным максимумом (минимумом) функции.
Ещё раз читаем вопрос задачи и выбираем нужный.
2) Определяем значения функции в точках максимума или минимума в соответствии с вопросом задачи.
3) Если точек максимума (минимума) на области определения функции несколько, то максимумы (минимумы) называются локальными, а самый большой (самый маленький) называется глобальным максимумом (минимумом) функции.
Ещё раз читаем вопрос задачи и выбираем нужный.
Слайд 18Задачи на определение наибольшего (наименьшего) значения функции на отрезке
1)Найти производную f'(x).
2)
Найти точки, в которых f'(x) не существует
3) Найти точки, в которых f'(x) = 0.
4) Отобрать точки, которые принадлежат данному отрезку.
5) Вычислить значение функции в критических точках и на концах отрезка, выбрать из них наибольшее или наименьшее значение.
Проговариваю, если критических точек нет, то наименьшее или наибольшее значение функция достигает на концах отрезка.
3) Найти точки, в которых f'(x) = 0.
4) Отобрать точки, которые принадлежат данному отрезку.
5) Вычислить значение функции в критических точках и на концах отрезка, выбрать из них наибольшее или наименьшее значение.
Проговариваю, если критических точек нет, то наименьшее или наибольшее значение функция достигает на концах отрезка.
Слайд 19Утверждения, полезные для отыскания наибольшего или наименьшего значения непрерывной функции y=f(x)
на промежутке (a; b)
1. Если функция y=f(x) имеет в промежутке (a; b) только одну точку экстремума с, причем эта точка максимума, то f(c) – наибольшее значение функции на промежутке.
2. Если функция y=f(x) имеет в промежутке (a; b) только одну точку экстремума с, причем эта точка минимума, то f(c) – наименьшее значение функции на промежутке.