- Главная
- Разное
- Образование
- Спорт
- Естествознание
- Природоведение
- Религиоведение
- Французский язык
- Черчение
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, фоны, картинки для презентаций
- Экология
- Экономика
Презентация, доклад на тему Проект на тему: Некоторые способы решения квадратных уравнений
Содержание
- 1. Проект на тему: Некоторые способы решения квадратных уравнений
- 2. Вступление.После изучения в школе квадратных уравнений мне
- 3. Квадратное уравнение.Квадратным уравнением называется уравнение вида ax²+bx+c=0,
- 4. Существует много способов решения квадратных уравнений. Среди
- 5. 1 способ. Решение по формуле. Сначала нужно
- 6. Пример.Решим квадратное уравнение 2x²-5x+2=0 по формулеD=b²-4ac=(-5)²-4*2*2=25-16=9X₁=-b-√D ;
- 7. 2 способ. Разложение левой части уравнения на
- 8. 3 способ. С использованием формул Виета. Этот
- 9. Пример.Решим квадратное уравнение x²+8x+7=0 по теореме Виета.Согласно
- 10. 4 способ. Способ «переброски».Если в квадратном уравнении
- 11. Пример.Решим квадратное уравнение 2x²-11x+15=0 способом «переброски». Перебросим
- 12. 5 способ. Графический способ. Если в квадратном
- 13. Пример.Решим уравнение x²-2x+1=0 графическим способом.X²=2x-1Построим параболу y=x²
- 14. Я решила дать ученикам 9 класса следующее
- 15. Результаты выполнения задания я занесла в таблицу.
- 16. Преимущества и недостатки применения некоторых способов решения квадратных уравнений.
- 17. Заключение.В ходе своей проектной работы я достигла
- 18. Использованная литература.В ходе своей исследовательской работы я
Слайд 2Вступление.
После изучения в школе квадратных уравнений мне стало интересно, сколько бывает
Цель работы:
Узнать, какие бывают способы решения квадратных уравнений, изучить их и научиться применять их на практике.
Задачи:
дать понятие квадратного уравнения;
изучить некоторые способы решения квадратных уравнений;
выявить наиболее удобные способы решения квадратных уравнений;
провести анкетирование среди учащихся 9 класса;
сделать вывод на основе представленного материала.
Слайд 3Квадратное уравнение.
Квадратным уравнением называется уравнение вида ax²+bx+c=0, где x- переменная, a,b,c-
Неполные квадратные уравнения бывают 3 видов:
ax²+c=0, где c не равно нулю
аx²+bx=0, где b не равно нулю
аx² = 0
Рассмотрим полные квадратные уравнения и способы их решения.
Слайд 4Существует много способов решения квадратных уравнений. Среди них:
Разложение левой части уравнения
Метод выделения полного квадрата
Решение по формуле
С использованием формул Виета
Способом «переброски»
По свойствам коэффициентов
Графический способ
С помощью циркуля и линейки
С помощью номограммы
Геометрический способ
Слайд 51 способ. Решение по формуле.
Сначала нужно найти дискриминант уравнения ax²+bx+c=0.
Если D > 0, то уравнение имеет 2 корня.
Если D < 0, то уравнение не имеет корней.
Если D = 0, то уравнение имеет один корень.
После этого можно найти корни уравнения. Они ищутся по формулам: x₁ = -b-√D ; x₂ = -b+√D
2a 2а
Полученные x₁ и x₂ и будут являться корнями уравнения.
Слайд 6Пример.
Решим квадратное уравнение 2x²-5x+2=0 по формуле
D=b²-4ac=(-5)²-4*2*2=25-16=9
X₁=-b-√D ; x₂=-b+√D
X₁=5-3/2*2=2/4=0,5
X₂=5+3/2*2=8/4=2
Ответ: корни квадратного уравнения: 0,5 и 2.
Слайд 72 способ. Разложение левой части уравнения на множители.
Для решения квадратного уравнения
Пример.
решим квадратное уравнение x²+10x-24=0 данным способом.
X²+12x-2x-24=0
X(x+12)-2(x+12)=0
(x+12)(x-2)=0
X+12=0 или x-2=0
X=-12 x=2
Ответ: корни квадратного уравнения: -12 и 2.
Слайд 83 способ. С использованием формул Виета.
Этот способ можно применять только
Согласно теореме Виета: сумма корней уравнения должна равняться коэффициенту b с противоположным знаком, а произведение корней должно равняться коэффициенту c.
x₁+x₂=-b
x₁*x₂=c
Слайд 9Пример.
Решим квадратное уравнение x²+8x+7=0 по теореме Виета.
Согласно теореме Виета:
x₁+x₂=-8
Значит: x₁=-7, а x₂=-1.
Проверка:
-7+(-1)=-8, верно
-7*(-1)=7, верно.
Слайд 104 способ. Способ «переброски».
Если в квадратном уравнении ax²+bx+c=0 умножить обе части
В выведенном квадратном уравнении нужно найти корни y₁ и y₂.
После этого можно найти корни x₁ и x₂ квадратного уравнения ax²+bx+c=0 по формуле x=y/a.
В данном способе решения квадратных уравнений коэффициент a умножается на свободный член, перебрасывается к нему, поэтому этот способ называется способом «переброски».
Слайд 11Пример.
Решим квадратное уравнение 2x²-11x+15=0 способом «переброски». Перебросим коэффициент 2 к свободному
По теореме Виета:
y₁+y₂=11
y₁*y₂=30
y₁=5, y₂=6
X=y/a
X₁=5/2=2,5
X₂=6/2=3 Ответ: корни квадратного
уравнения 2,5 и 3.
Слайд 125 способ. Графический способ.
Если в квадратном уравнении x²+bx+c=0 второй и
В одной системе координат нужно построить графики: y= x²(парабола) и y=-bx-c( прямая). Абсциссы точек пересечения будут являться корнями квадратного уравнения.
Если парабола и прямая имеют 2 точки пересечения, то квадратное уравнение имеет 2 корня.
Если парабола и прямая имеют 1 точку пересечения, то квадратное уравнение имеет только 1 корень.
Если парабола и прямая не пересекаются, то квадратное уравнение не имеет корней.
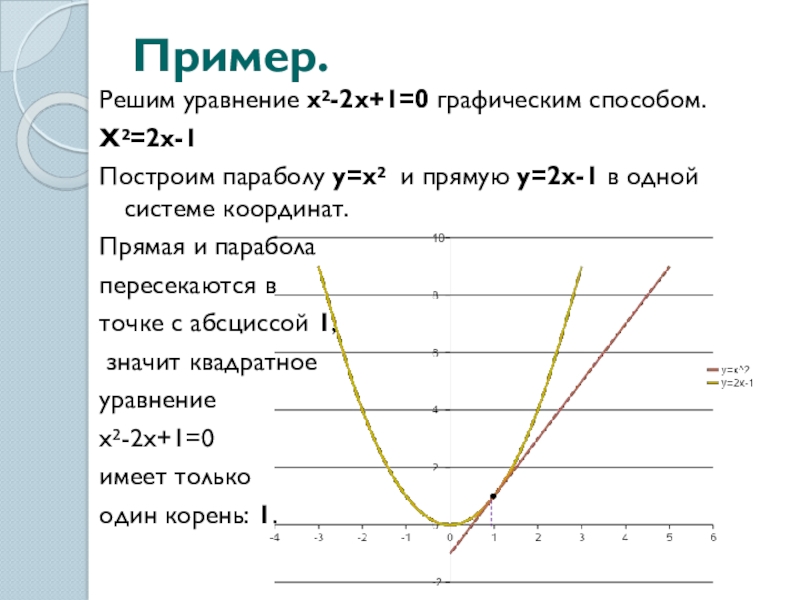
Слайд 13Пример.
Решим уравнение x²-2x+1=0 графическим способом.
X²=2x-1
Построим параболу y=x² и прямую y=2x-1 в
Прямая и парабола
пересекаются в
точке с абсциссой 1,
значит квадратное
уравнение
x²-2x+1=0
имеет только
один корень: 1.
Слайд 14Я решила дать ученикам 9 класса следующее задание.
Решите квадратные уравнения любым из перечисленных способов:
по формуле,
разложение левой части уравнения на множители,
способ «переброски»,
графический способ,
с использованием формул Виета.
Уравнения:
x²+6x+9=0
6x²+5x+1=0
4x²+12x+5=0
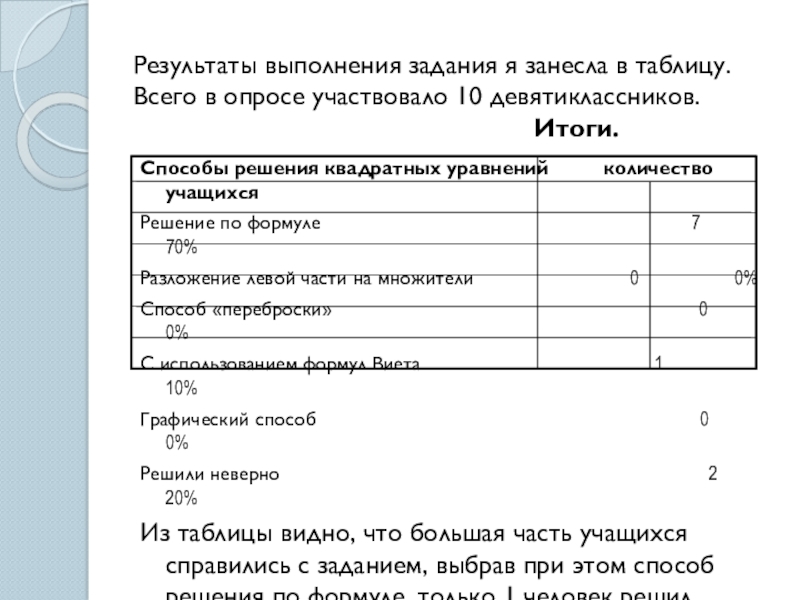
Слайд 15Результаты выполнения задания я занесла в таблицу. Всего в опросе участвовало
Способы решения квадратных уравнений количество учащихся
Решение по формуле 7 70%
Разложение левой части на множители 0 0%
Способ «переброски» 0 0%
С использованием формул Виета 1 10%
Графический способ 0 0%
Решили неверно 2 20%
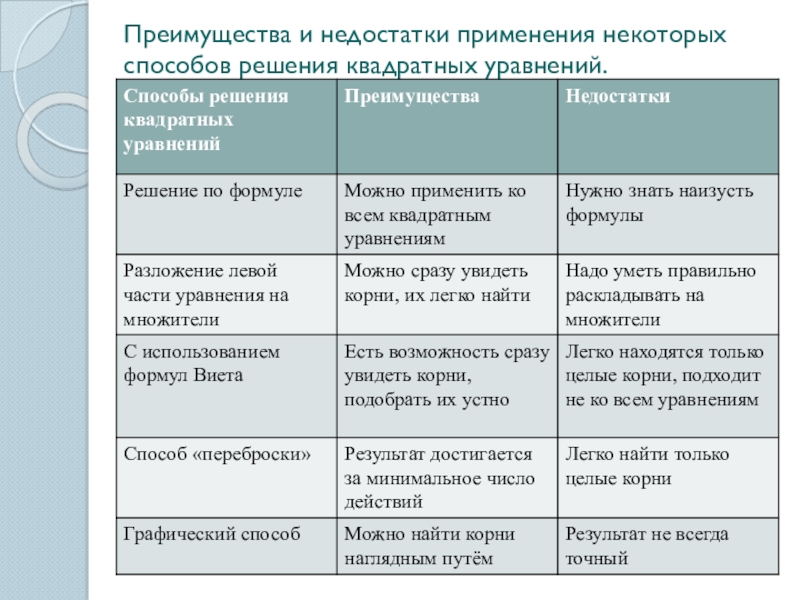
Из таблицы видно, что большая часть учащихся справились с заданием, выбрав при этом способ решения по формуле, только 1 человек решил уравнение с помощью теоремы Виета, и 20% учеников не справились с заданием. Рассмотрим преимущества и недостатки этих способов.