есть не только знание, но и сознание, т.е. Умение пользоваться знанием как следует.
Колючевский В.О.
- Главная
- Разное
- Образование
- Спорт
- Естествознание
- Природоведение
- Религиоведение
- Французский язык
- Черчение
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, фоны, картинки для презентаций
- Экология
- Экономика
Презентация, доклад на тему Призентация по математике на тему Преобразование графиков функции
Содержание
- 1. Призентация по математике на тему Преобразование графиков функции
- 2. Историческая справкаСлово «функция» происходит от латинского functio
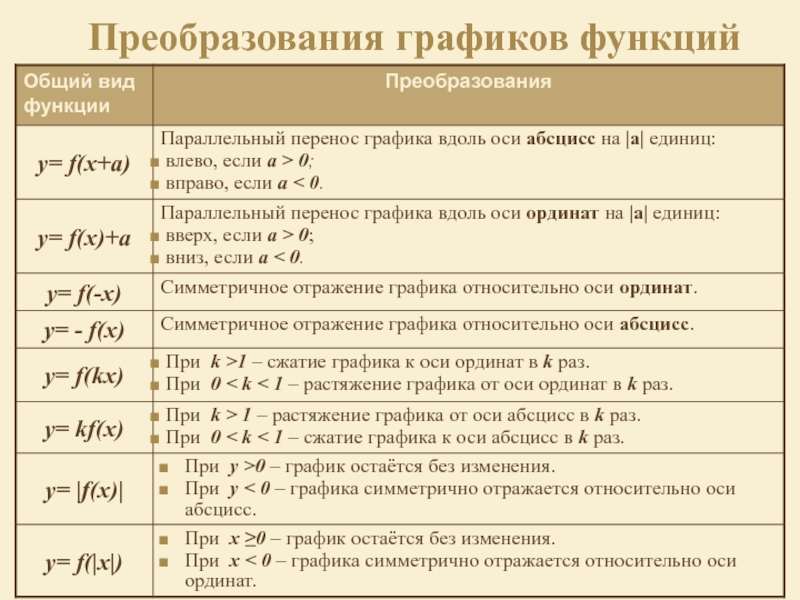
- 3. Преобразования графиков функций
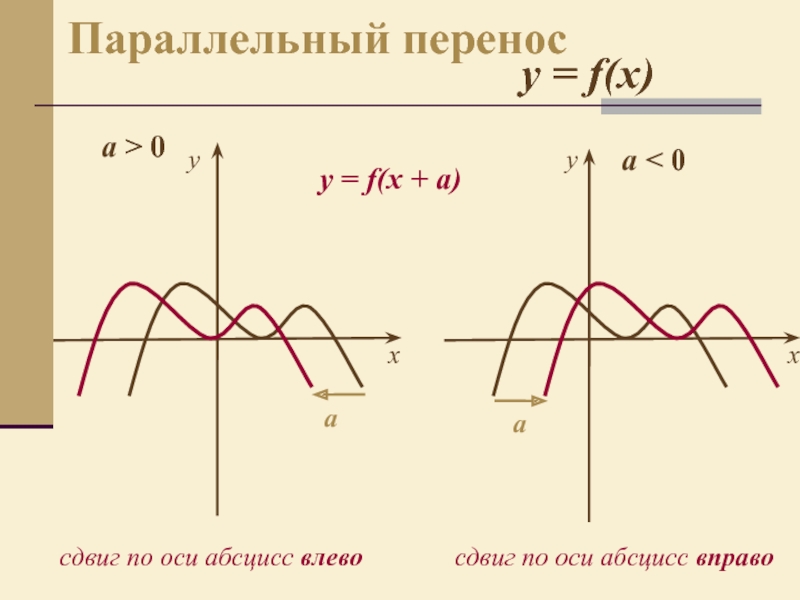
- 4. a > 0ayсдвиг по оси абсцисс вправоy
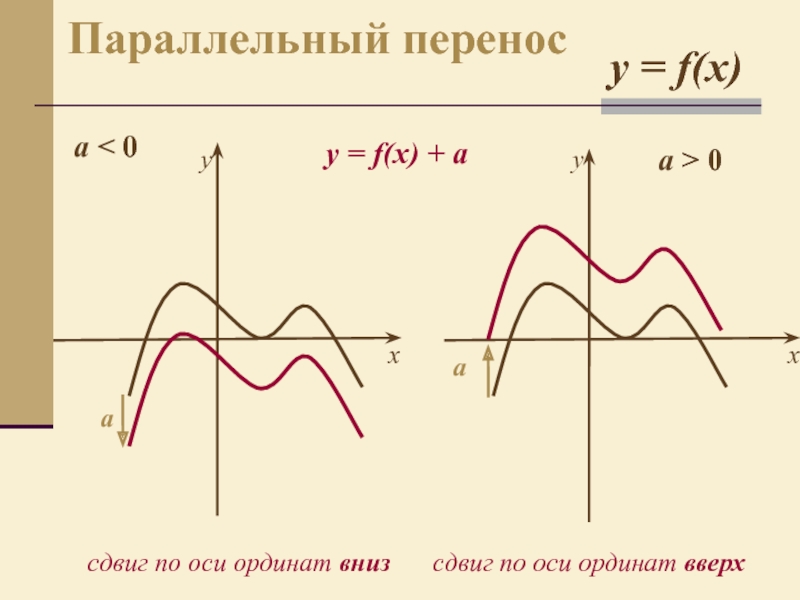
- 5. a > 0ayсдвиг по оси ординат внизy
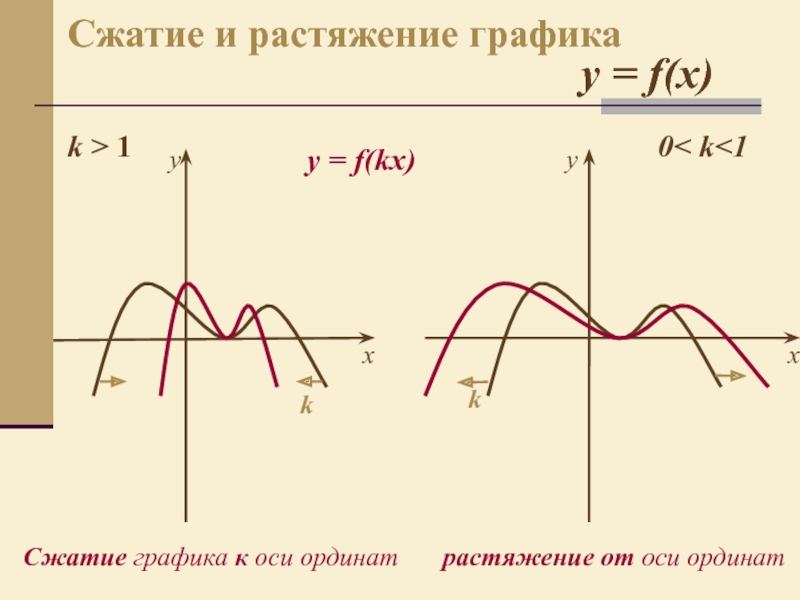
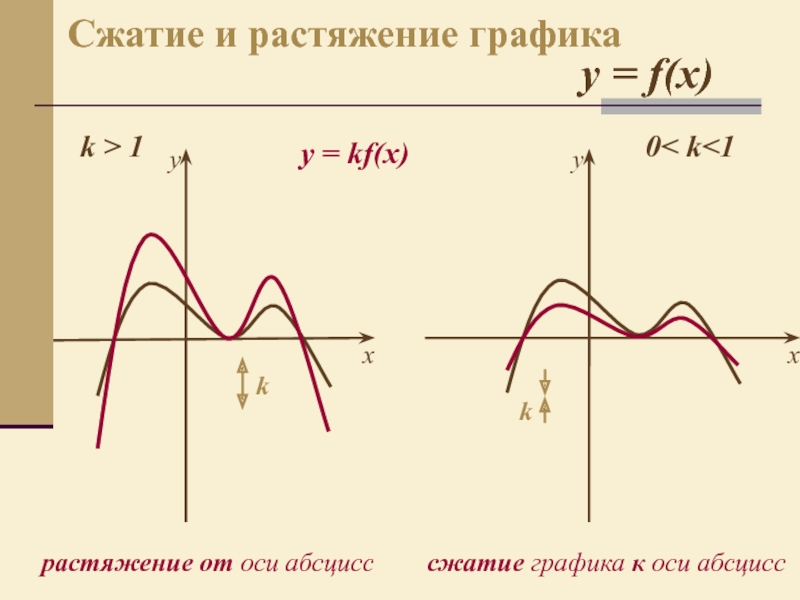
- 6. 0< k 1kСжатие и растяжение графикаk
- 7. 0< k 1kСжатие и растяжение графикаk
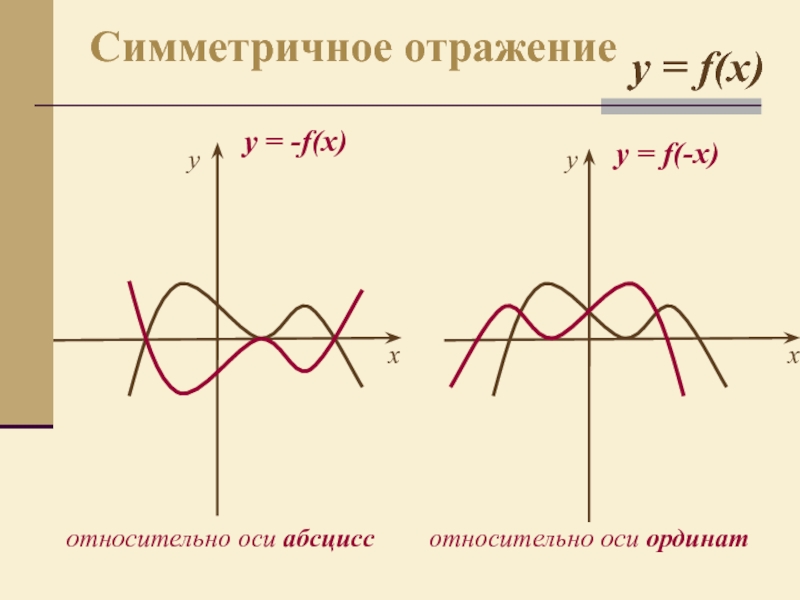
- 8. yотносительно оси абсциссy = -f(x) относительно оси ординат yххy = f(-x) Симметричное отражениеy = f(x)
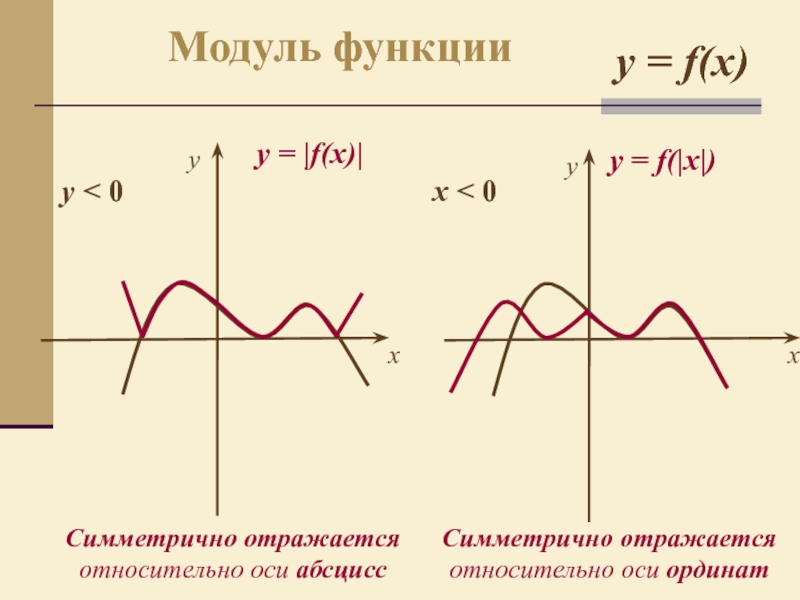
- 9. yy = f(|x|) Симметрично отражается относительно оси
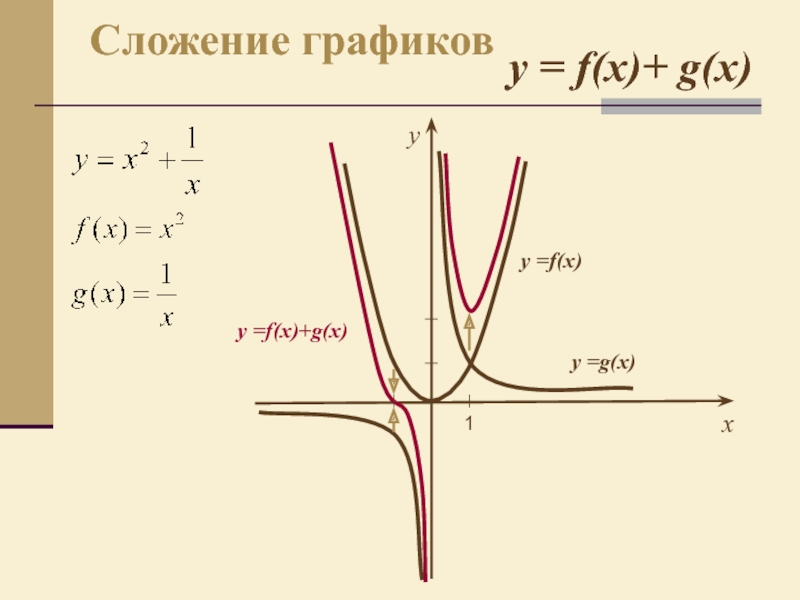
- 10. yх Сложение графиков y = f(x)+ g(x)у =f(x)у =g(x)у =f(x)+g(x)1
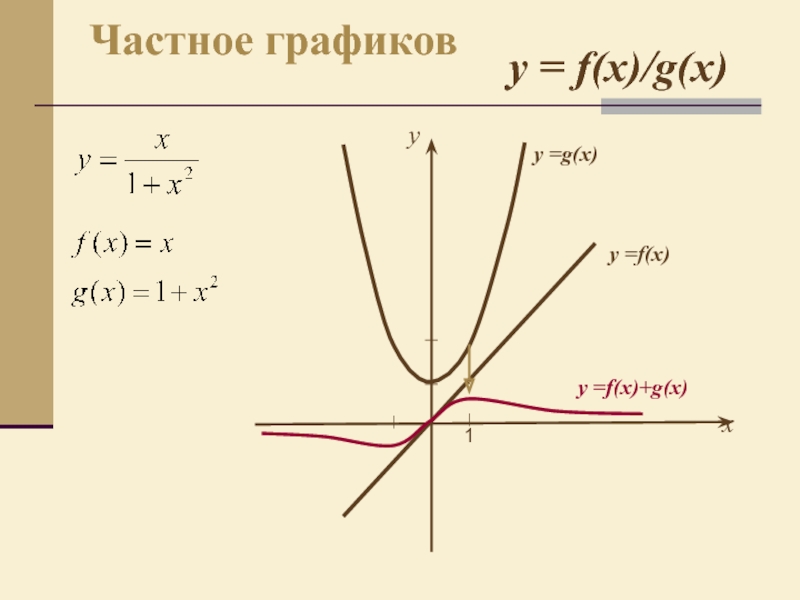
- 11. yх Частное графиков y = f(x)/g(x)у =g(x)у =f(x)у =f(x)+g(x)1
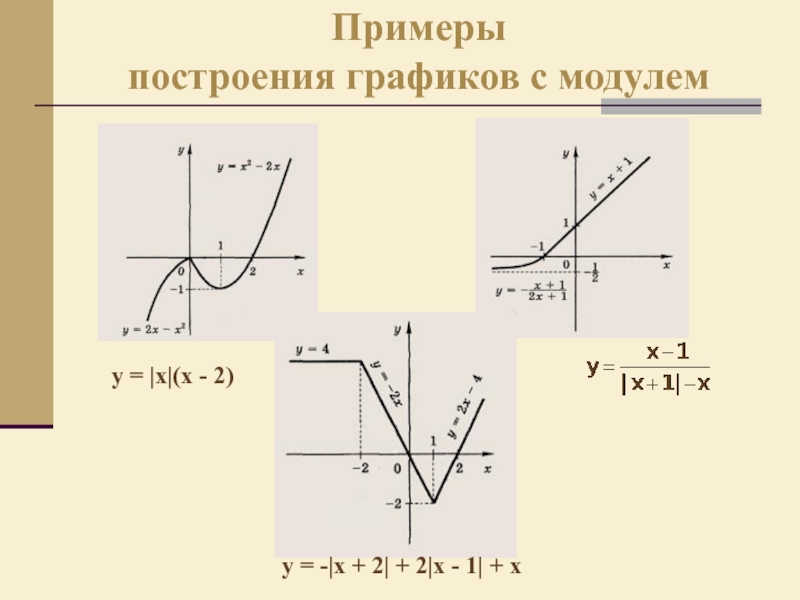
- 12. Примеры построения графиков с модулему =
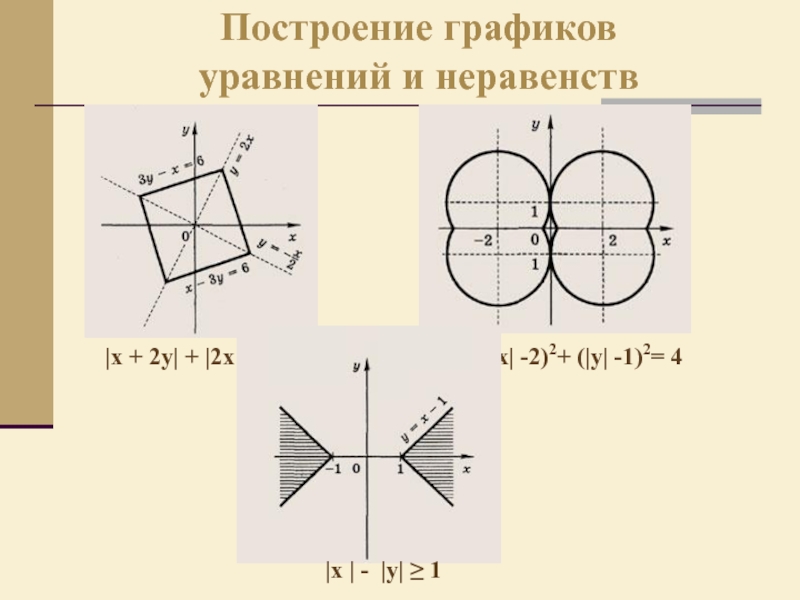
- 13. Построение графиков уравнений и неравенств|x +
- 14. Конец.Учитель математики МБОУ СОШ №85 Г.Воронеж Овчинникова Ольга Ильинична
Историческая справкаСлово «функция» происходит от латинского functio – исполнение, осуществление. Термин «функция» впервые появляется в 1692 году у Лейбница, и притом не совсем в современном его понимании. Лейбниц вначале называет функцией различные отрезки, связанные с какой-либо
Слайд 1Преобразование графиков функций
Науку часто смешивают с знанием. Это грубое недоразумение. Наука
Слайд 2Историческая справка
Слово «функция» происходит от латинского functio – исполнение, осуществление.
Термин
«функция» впервые появляется в 1692 году у Лейбница, и притом не совсем в современном его понимании. Лейбниц вначале называет функцией
различные отрезки,
связанные с
какой-либо
кривой (например,
абсциссы её точек).
различные отрезки,
связанные с
какой-либо
кривой (например,
абсциссы её точек).
Г.В. Лейбниц
Геродот
Слайд 4a > 0
a
y
сдвиг по оси абсцисс вправо
y = f(x)
сдвиг по оси
абсцисс влево
y
х
х
y = f(x + a)
a < 0
a
Параллельный перенос
Слайд 5a > 0
a
y
сдвиг по оси ординат вниз
y = f(x) + a
y
= f(x)
сдвиг по оси ординат вверх
y
х
х
a < 0
a
Параллельный перенос
Слайд 8
y
относительно оси абсцисс
y = -f(x)
относительно оси ординат
y
х
х
y = f(-x)
Симметричное отражение
y = f(x)
Слайд 9
y
y = f(|x|)
Симметрично отражается относительно оси абсцисс
y
х
х
y = |f(x)|
Модуль функции
y = f(x)
х < 0
y < 0
Симметрично отражается относительно оси ординат
Слайд 13Построение графиков
уравнений и неравенств
|x + 2y| + |2x - y|
= 6
(|х| -2)2+ (|у| -1)2= 4
|x | - |y| ≥ 1
