Шустрова Оксана Сергевна
- Главная
- Разное
- Образование
- Спорт
- Естествознание
- Природоведение
- Религиоведение
- Французский язык
- Черчение
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, фоны, картинки для презентаций
- Экология
- Экономика
Презентация, доклад на тему Применение производной к исследованию и построению графиков функций
Содержание
- 1. Применение производной к исследованию и построению графиков функций
- 2. Цель урока:научиться применять таблицу производных при исследовании функций и построении графиков
- 3. Математический диктантВариант 1.(Cu)’=……=(u’v-v’u)/v²(cos x)’=……=1/cos² x(ex)’=…Вариант 2.C’=……=(u’v+v’u)(sin x)’=……=-1/sin²
- 4. Классная работаОдной из основных задач, возникающих при
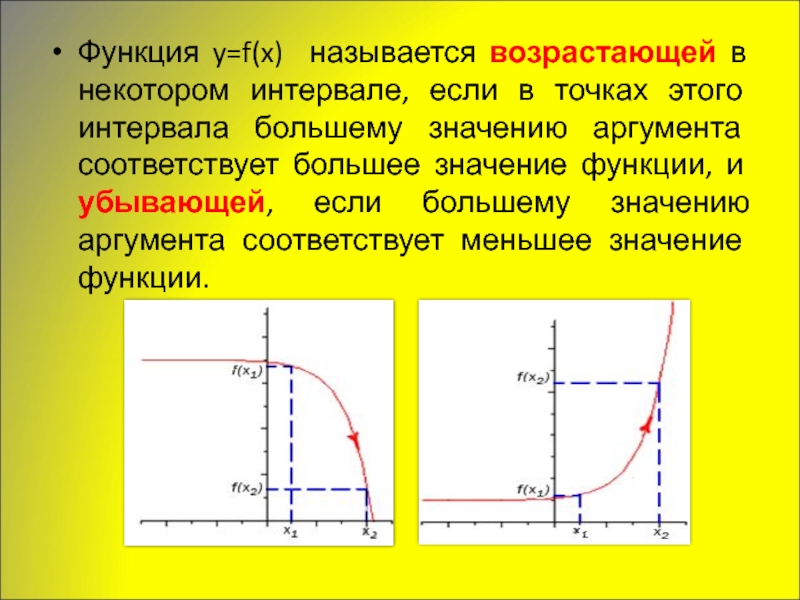
- 5. Функция y=f(x) называется возрастающей в некотором интервале,
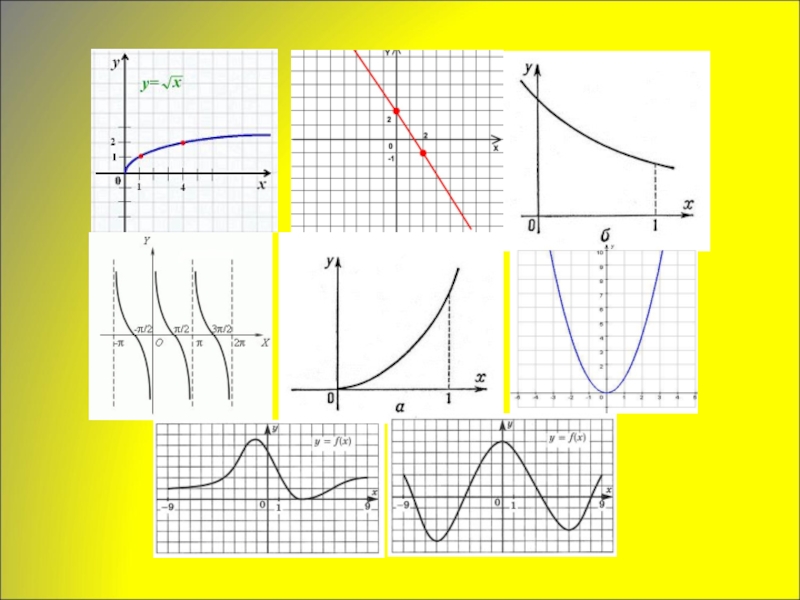
- 6. возрастающаяубывающаяубывающаяубывающаявозрастающаявозрастающая и убывающая на интервалахвозрастающая и убывающая на интервалахвозрастающая и убывающая на интервалах
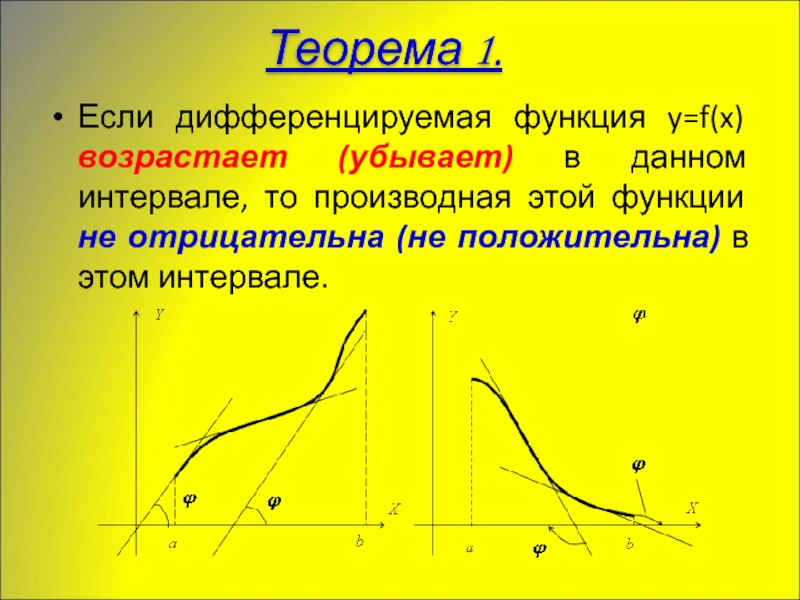
- 7. Если дифференцируемая функция y=f(x) возрастает (убывает) в
- 8. Если производная функции y=f(x) положительна (отрицательна) на
- 9. Находим область определения функции f(x).Вычисляем производную f’(x)
- 10. Область определения: R. Функция непрерывна.Вычисляем производную :
- 11. Область определения: R. Функция непрерывна.Вычисляем производную :
- 12. Точку x=x0 называют точкой минимума функции y=f(x),
- 13. Если функция y=f(x) имеет экстремум в точке
- 14. Если производная f’(x) при переходе через точку
- 15. Область определения: R. Функция непрерывна.Вычисляем производную :
- 16. Работа на уроке: № 564. Исследовать на
- 17. № 565. Исследовать на экстремум функцию
- 18. № 566. Исследовать на экстремум функцию
- 19. № 571. Исследовать на экстремум функцию
- 20. Учебник Лисичкин В. Т., Соловейчик И. Л.:
Слайд 1Урок-лекция «Применение производной к исследованию и построению графиков функций» урок
Слайд 2Цель урока:
научиться применять таблицу производных при исследовании функций и построении графиков
Слайд 3Математический диктант
Вариант 1.
(Cu)’=…
…=(u’v-v’u)/v²
(cos x)’=…
…=1/cos² x
(ex)’=…
Вариант 2.
C’=…
…=(u’v+v’u)
(sin x)’=…
…=-1/sin² x
(xn)’=…
Вариант 1.
(Cu)’=Cu’
(u/v)=(u’v-v’u)/v²
(cos x)’=-sin x
tg
(ex)’=ex
Вариант 2.
C’=0
(uv)’=(u’v+v’u)
(sin x)’=cos x
ctg x=-1/sin² x
(xn)’=n*xn-1
Слайд 4Классная работа
Одной из основных задач, возникающих при исследовании функции, является нахождение
Слайд 5Функция y=f(x) называется возрастающей в некотором интервале, если в точках этого
Слайд 6возрастающая
убывающая
убывающая
убывающая
возрастающая
возрастающая и убывающая
на интервалах
возрастающая и убывающая
на интервалах
возрастающая и убывающая
Слайд 7Если дифференцируемая функция y=f(x) возрастает (убывает) в данном интервале, то производная
Теорема 1.
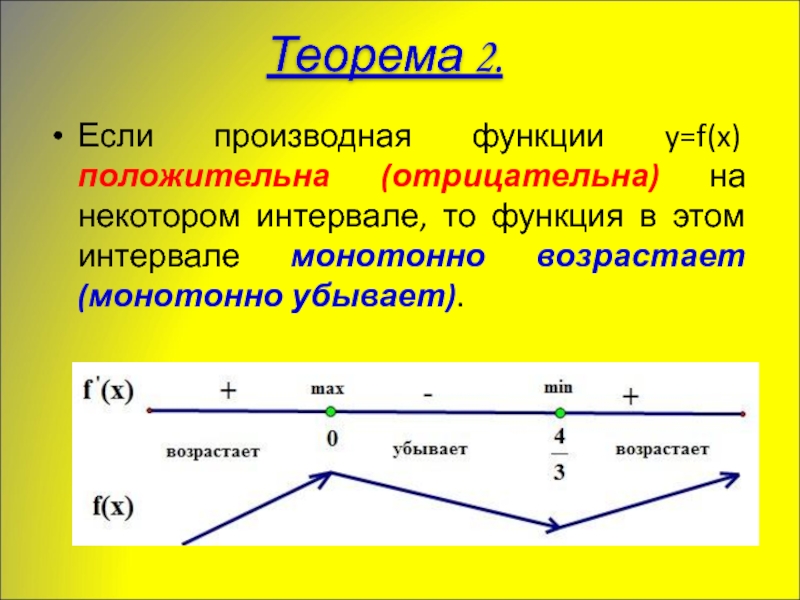
Слайд 8Если производная функции y=f(x) положительна (отрицательна) на некотором интервале, то функция
Теорема 2.
Слайд 9Находим область определения функции f(x).
Вычисляем производную f’(x) данной функции.
Находим точки, в
Делим область определения функции этими точками на интервалы. Они являются интервалами монотонности.
Исследуем знак f’(x) на каждом интервале. Если f’(x)›0, то на этом интервале f(x) возрастает; если f’(x)‹0, то на таком интервале функция f(x) убывает.
Правило нахождения интервалов
монотонности
Слайд 10Область определения: R. Функция непрерывна.
Вычисляем производную : y’=6x²-6x-36.
Находим критические точки: y’=0.
x²-x-6=0
Д=1-4*(-6)*1=1+24=25
Делим область определения на интервалы:
Функция возрастает при xϵ(-∞;-2]υ[3;+∞), функция убывает при xϵ[-2;3].
Пример №1. Найти промежутки монотонности функции y=2x³-3x²-36x+5
Слайд 11Область определения: R. Функция непрерывна.
Вычисляем производную : y’=3x²-6x.
Находим критические точки: y’=0.
x²-2x=0
x(x-2)=0
x1=0 и x2=2
Делим область определения на интервалы:
Функция возрастает при xϵ(-∞;0]υ[2;+∞), функция убывает при xϵ[0;2].
Пример №2. Найти промежутки монотонности функции y=x³-3x²
Слайд 12Точку x=x0 называют точкой минимума функции y=f(x), если у этой точки
Точку x=x0 называют точкой максимума функции y=f(x), если у этой точки существует окрестность, для всех точек которой выполняется неравенство f(x)≤f(x0).
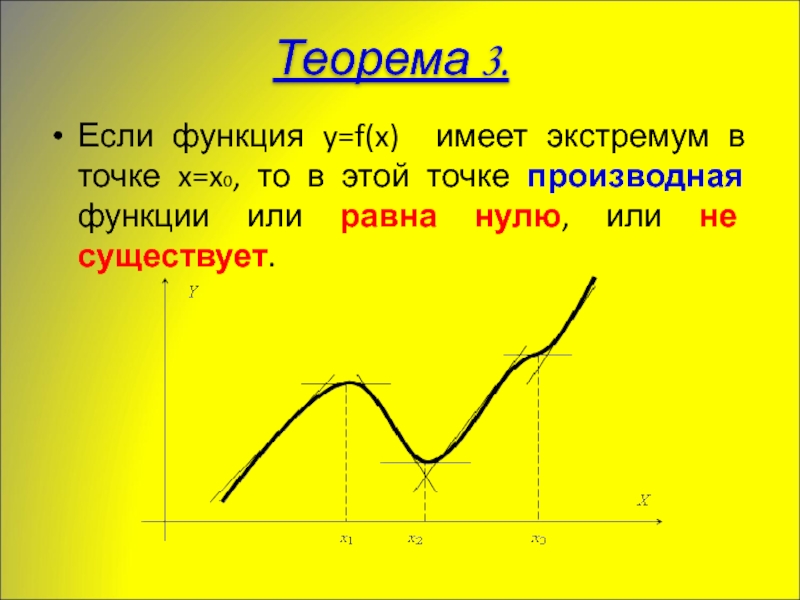
Слайд 13Если функция y=f(x) имеет экстремум в точке x=x0, то в этой
Теорема 3.
Слайд 14Если производная f’(x) при переходе через точку x0 меняет знак, то
Если производная меняет знак с + на –, то точка будет являться точкой максимума, если с – на +, то точка будет точкой минимума
Теорема 4.
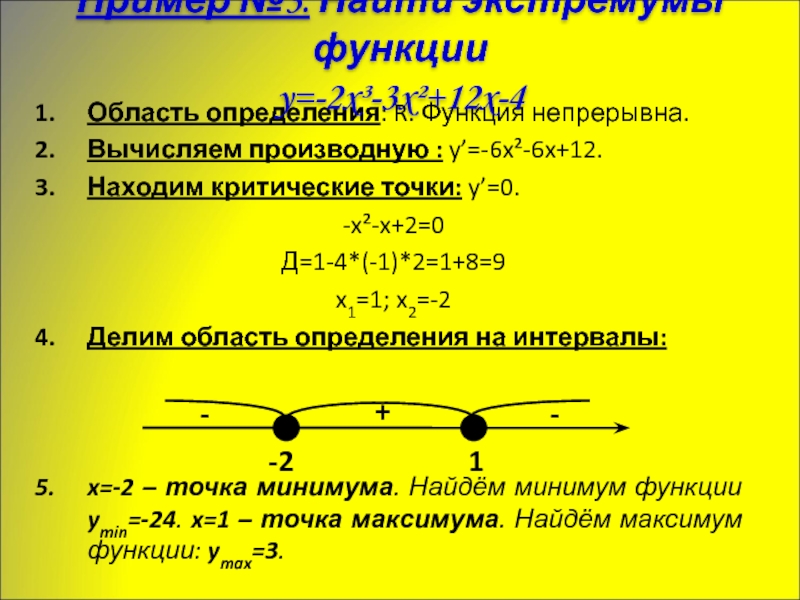
Слайд 15Область определения: R. Функция непрерывна.
Вычисляем производную : y’=-6x²-6x+12.
Находим критические точки: y’=0.
-x²-x+2=0
Д=1-4*(-1)*2=1+8=9
x1=1; x2=-2
Делим область определения на интервалы:
x=-2 – точка минимума. Найдём минимум функции ymin=-24. x=1 – точка максимума. Найдём максимум функции: ymax=3.
Пример №3. Найти экстремумы функции
y=-2x³-3x²+12x-4
Слайд 16Работа на уроке:
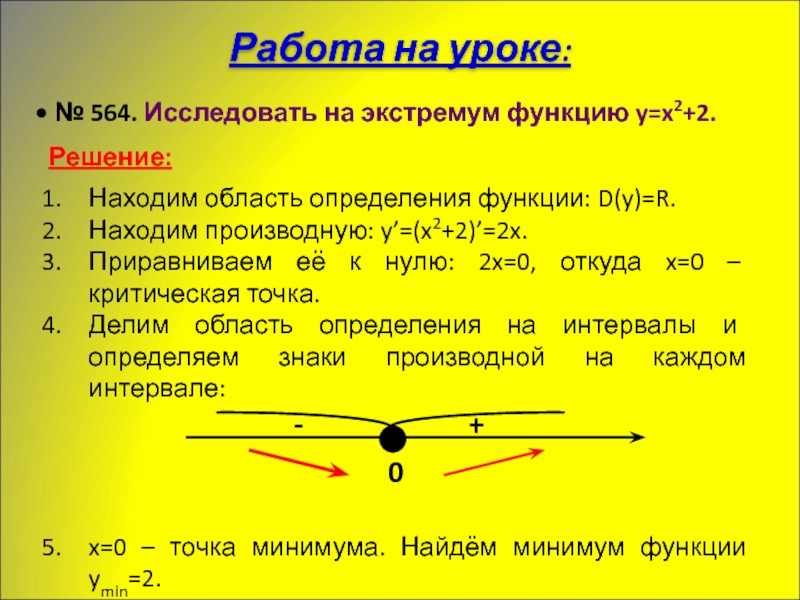
№ 564. Исследовать на экстремум функцию y=x2+2.
Решение:
Находим область
Находим производную: y’=(x2+2)’=2x.
Приравниваем её к нулю: 2x=0, откуда x=0 – критическая точка.
Делим область определения на интервалы и определяем знаки производной на каждом интервале:
x=0 – точка минимума. Найдём минимум функции ymin=2.
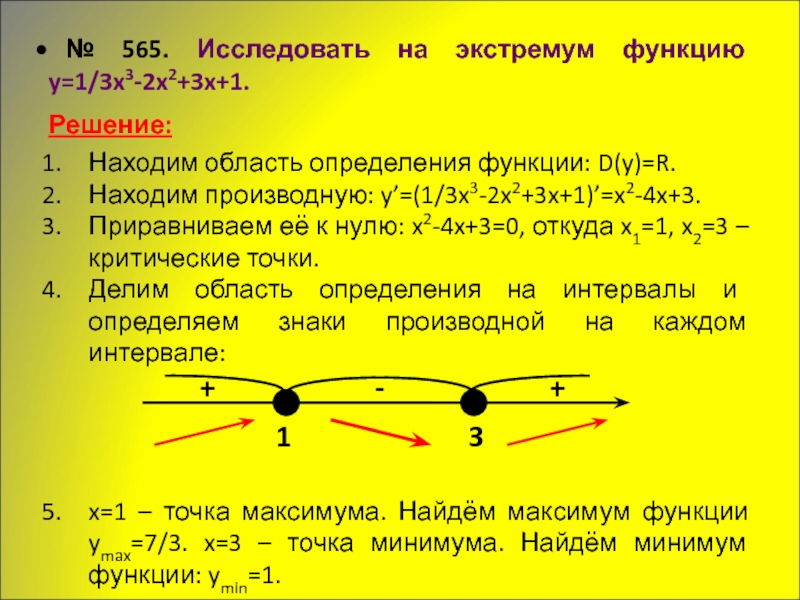
Слайд 17 № 565. Исследовать на экстремум функцию
y=1/3x3-2x2+3x+1.
Решение:
Находим область определения функции:
Находим производную: y’=(1/3x3-2x2+3x+1)’=x2-4x+3.
Приравниваем её к нулю: x2-4x+3=0, откуда x1=1, x2=3 – критические точки.
Делим область определения на интервалы и определяем знаки производной на каждом интервале:
x=1 – точка максимума. Найдём максимум функции ymax=7/3. x=3 – точка минимума. Найдём минимум функции: ymin=1.
Слайд 18 № 566. Исследовать на экстремум функцию
y=x3+3x2+9x-6.
Решение:
Находим область определения функции:
Находим производную: y’=(x3+3x2+9x-6)’=3x2+6x+9.
Приравниваем её к нулю: 3x2+6x+9=0, откуда D<0. То есть критических точек не существует.
Однако, функция возрастает на всей D(y), так как y’=3x2+6x+9 >0:
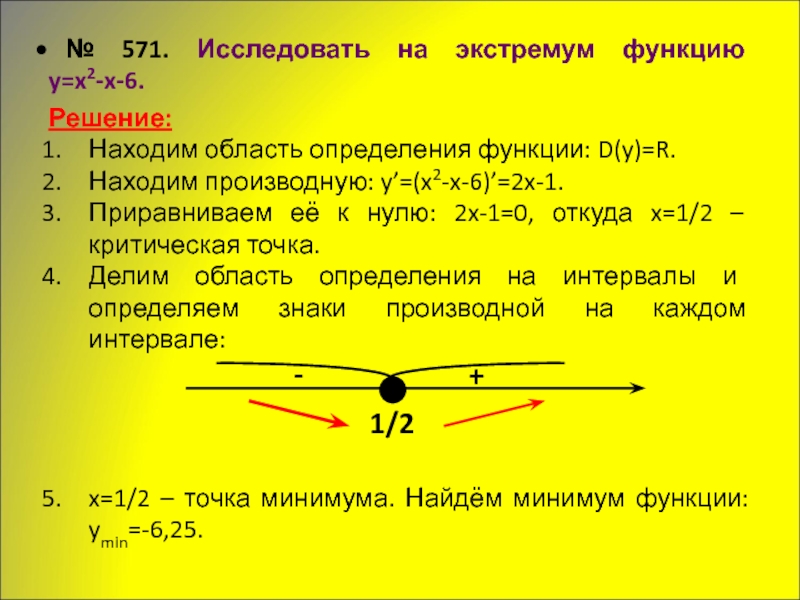
Слайд 19 № 571. Исследовать на экстремум функцию
y=x2-x-6.
Решение:
Находим область определения функции:
Находим производную: y’=(x2-x-6)’=2x-1.
Приравниваем её к нулю: 2x-1=0, откуда x=1/2 – критическая точка.
Делим область определения на интервалы и определяем знаки производной на каждом интервале:
x=1/2 – точка минимума. Найдём минимум функции: ymin=-6,25.
Слайд 20Учебник Лисичкин В. Т., Соловейчик И. Л.: № 572, 573, 575,
Выучить достаточные и необходимые условия монотонности и существования экстремумов функции.
Задание на дом: