- Главная
- Разное
- Образование
- Спорт
- Естествознание
- Природоведение
- Религиоведение
- Французский язык
- Черчение
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, фоны, картинки для презентаций
- Экология
- Экономика
Презентация, доклад Жизнь замечательных людей, Внеклассное мероприятие Леонард Эйлер
Содержание
- 1. Презентация, Жизнь замечательных людей, Внеклассное мероприятие Леонард Эйлер
- 2. Эйлер принадлежит к числу гениев, чьё творчество
- 3. Эйлер принадлежит к числу гениев, чьё творчество
- 4. Леонард родился 15 апреля 1707 г. в
- 5. Когда Леонарду едва исполнилось 13 лет,
- 6. Уже 17 лет от роду Леонард получил
- 7. Первыми в Санкт-Петербург перебрались Даниил и Николай,
- 8. В столице Российской Империи молодого спеца, меньше
- 9. 27 декабря 1733 года 26-летний Леонард Эйлер
- 10. За первый период пребывания в России он
- 11. В 1735 году Академия получила задание выполнить
- 12. Бывший учитель, Иоганн Бернулли, писал ему: «Я
- 13. В 1748 г. выходит в свет научный
- 14. Многочисленные статьи по отдельным вопросам печатаются в
- 15. В 1765 году опубликована «Теория движения твёрдых
- 16. 17 (28) июля 1766 года 60-летний Эйлер,
- 17. В эти же годы вышли трёхтомник «Диоптрика»
- 18. В 1771 году в жизни Эйлера произошли
- 19. В 1779 году опубликована «Всеобщая сферическая тригонометрия»,
- 20. Эйлер внес большой вклад в алгебру и
- 21. Используя специально подобранную символику, Эйлер облегчил язык
- 22. Функция Эйлера ϕ(n) показывает, сколько натуральных чисел
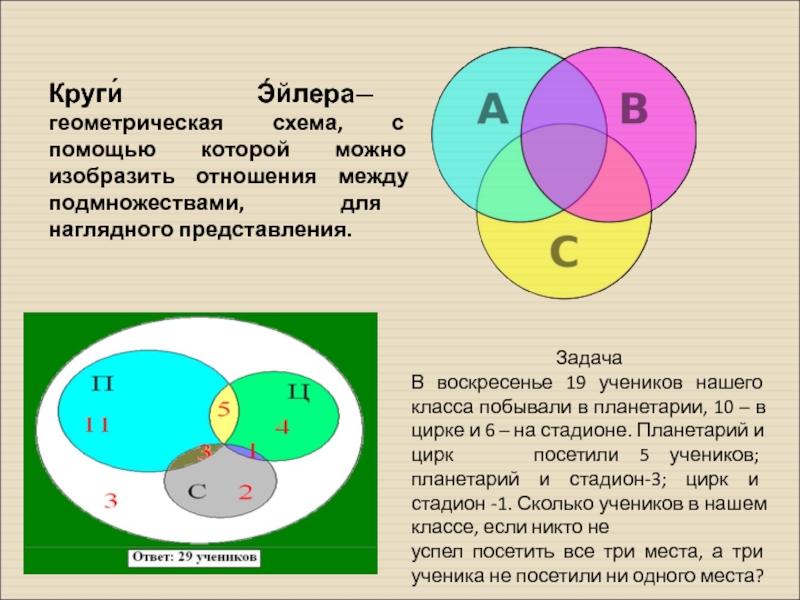
- 23. Круги́ Э́йлера— геометрическая схема, с помощью которой
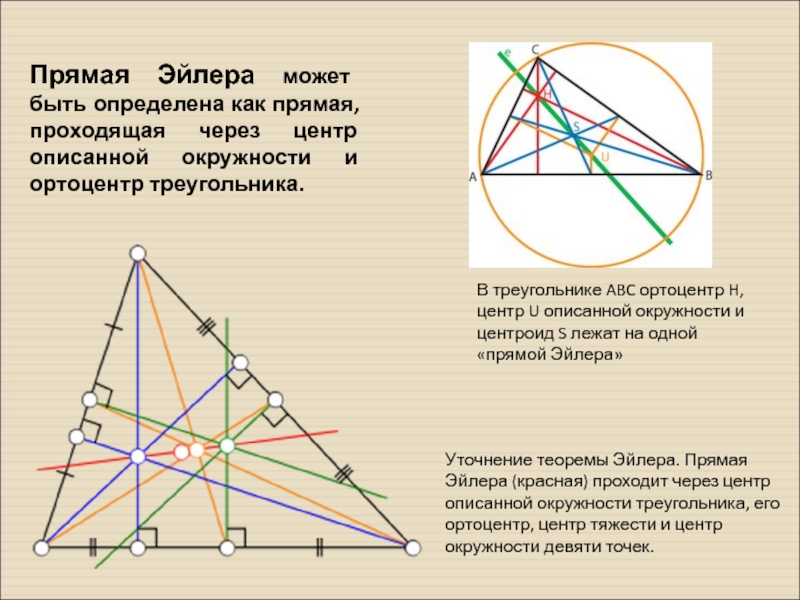
- 24. Прямая Эйлера может быть определена как прямая,
- 25. Теорема Эйлера о многогранниках:
- 26. Формула Эйлера для комплексных чисел
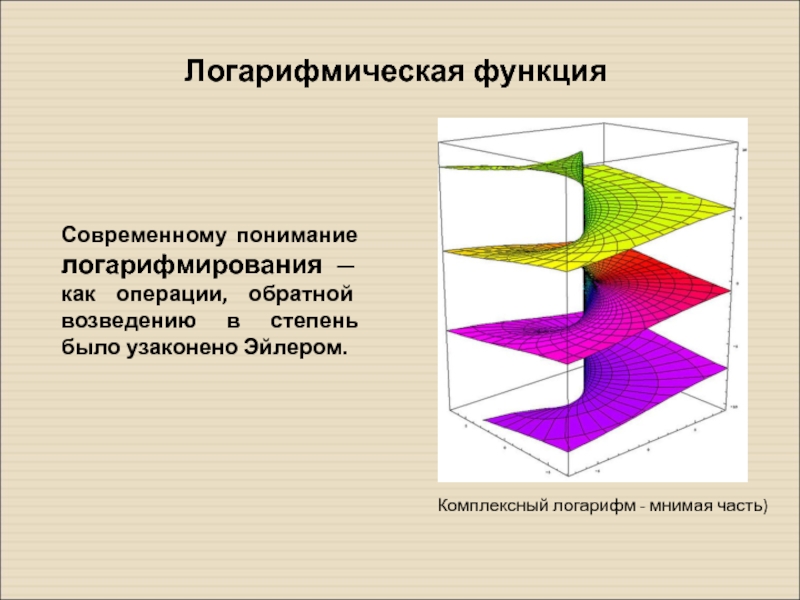
- 27. Комплексный логарифм - мнимая часть)Современному понимание
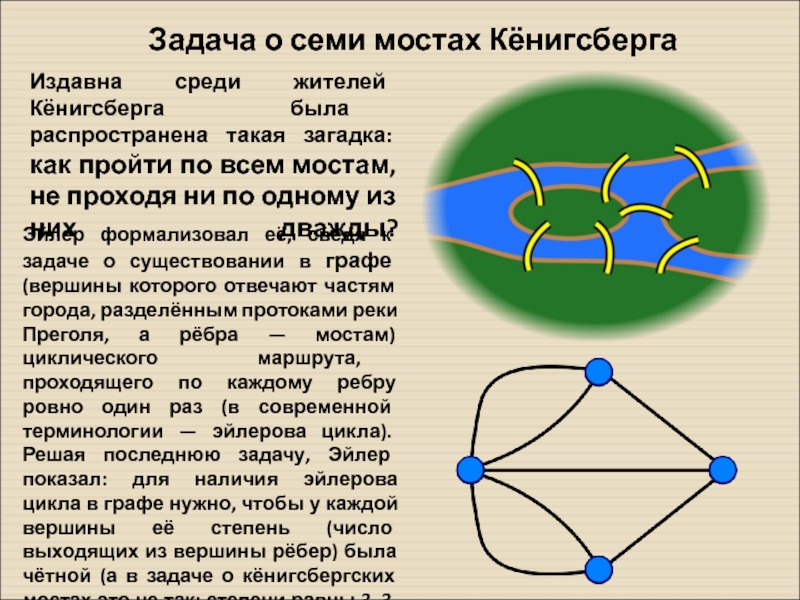
- 28. Задача о семи мостах КёнигсбергаИздавна среди жителей
- 29. Дети математика так и остались в России.
- 30. Источники иллюстрацийИнтернет :Google картинки - http://physiclib.ru,
Слайд 1Калейдоскоп интересных мгновений из жизни выдающихся математиков
Леонард Эйлер
Leonhard Euler
Подготовила преподаватель
Слайд 2Эйлер принадлежит к числу гениев, чьё творчество стало достоянием всего человечества.
До сих пор школьники всех стран изучают тригонометрию и
логарифмы в том виде, какой
придал им Эйлер. Студенты проходят высшую математику по руководствам, первыми образцами которых явились классические монографии Эйлера. Он был , прежде всего, математиком, но он знал, что
почвой, на которой расцветает математика, является
практическая деятельность.
(1707-1783)
Слайд 3Эйлер принадлежит к числу гениев, чьё творчество стало достоянием всего человечества.
Слайд 4Леонард родился 15 апреля 1707 г. в Швейцарии в семье пастора
Начальное обучение мальчик прошел дома под руководством отца, учившегося некогда математике у Якоба Бернулли. Пастор готовил сына к духовной карьере, однако занимался с ним и точными науками – как в качестве развлечения, так и для развития логического мышления. У мальчика проявился интерес к учёбе, и его направили для получения образования в Базельскую латинскую гимназию.
Якоб Бернулли
Иоганн Бернулли
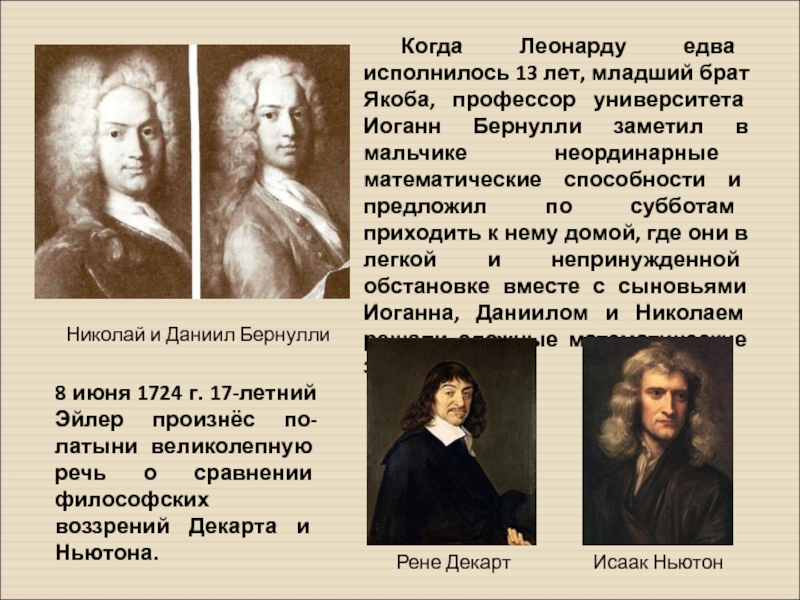
Слайд 5 Когда Леонарду едва исполнилось 13 лет, младший брат Якоба, профессор
Николай и Даниил Бернулли
8 июня 1724 г. 17-летний Эйлер произнёс по-латыни великолепную речь о сравнении философских воззрений Декарта и Ньютона.
Рене Декарт
Исаак Ньютон
Слайд 6Уже 17 лет от роду Леонард получил ученую степень магистра. Вскоре
Базельский университет
в XVII—XVIII веках
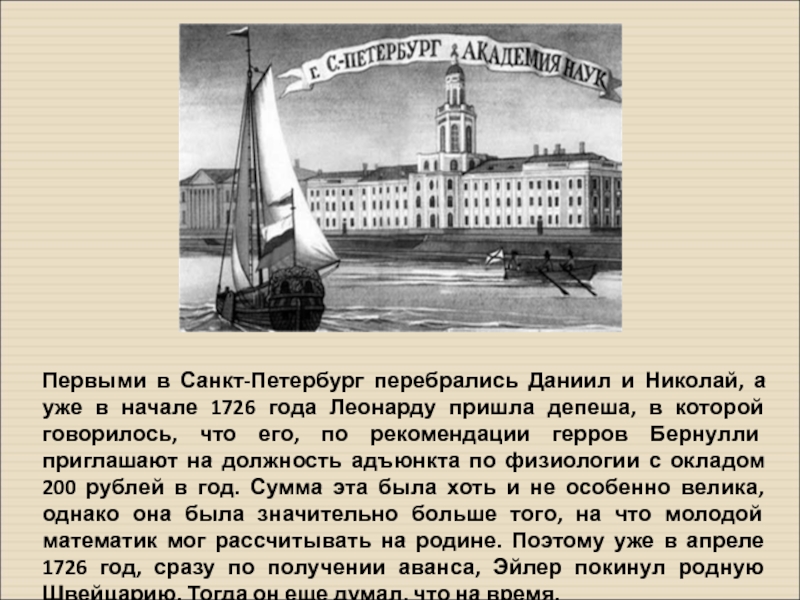
Слайд 7Первыми в Санкт-Петербург перебрались Даниил и Николай, а уже в начале
Слайд 8В столице Российской Империи молодого спеца, меньше чем за год научившегося
Слайд 927 декабря 1733 года 26-летний Леонард Эйлер женился на своей ровеснице
Слайд 10За первый период пребывания в России он написал более 90 крупных
Слайд 11В 1735 году Академия получила задание выполнить срочное и очень громоздкое
Двухтомное сочинение «Механика, или наука о движении, изложенная аналитически», изданное в 1736 году, принесло Эйлеру общеевропейскую известность. В этой монографии Эйлер с успехом применил методы математического анализа к общему решению проблем движения в пустоте и в сопротивляющейся среде.
«Тот, кто имеет достаточные навыки в анализе, сможет всё увидеть с необычайной лёгкостью и без всякой помощи прочитает работу полностью», - заканчивает Эйлер своё предисловие к книге.
Слайд 12Бывший учитель, Иоганн Бернулли, писал ему: «Я посвятил себя детству высшей
Фридрих II Прусский
29 мая 1741 года Академия наук отпустила Эйлера по его просьбе и утвердила почётным членом Академии с окладом 200 рублей. В июне 1741 года 34-летний Леонард Эйлер с женой, двумя сыновьями и четырьмя племянниками прибыл в Берлин. Он провёл там 25 лет и издал около 260 работ.
«Того ради нахожусь принужден, как ради слабого здоровья, так и других обстоятельств, искать приятнейшего климата и принять от его Королевского Величества Прусского учиненное мне призывание. Того ради прошу Императорскую Академию наук всеподданнейше меня милостиво уволить и снабдить для моего и домашних моих проезду потребным пашпортом»
Слайд 13В 1748 г. выходит в свет научный труд учёного «Введение в
«Морская наука» (1749 г.),
«Теория движения луны» (1753 г.),
«Наставление по дифференциальному исчислению» (1755 г.)
В 1757 г. Эйлер впервые в истории нашёл формулы для определения критической нагрузки при сжатии упругого стержня. Однако в те годы эти формулы не нашли применения.
Почти сто лет спустя, когда во многих странах – и прежде всего в Англии – стали строить железные дороги, потребовалось рассчитать прочность железнодорожных мостов. Модель Эйлера принесла практическую пользу в проведении экспериментов.
Слайд 14Многочисленные статьи по отдельным вопросам печатаются в изданиях Берлинской и Петербургской
Все годы пребывания в Германии Эйлер сохранял связь с Россией. Эйлер участвовал в публикациях Петербургской Академии, приобретал для неё книги и инструменты, редактировал математические отделы русских журналов. На его квартире, на полном пансионе, годами жили молодые русские учёные, командированные на стажировку. Известно об оживлённой переписке Эйлера с М. В. Ломоносовым, в творчестве которого он высоко ценил «счастливое сочетание теории с экспериментом». Этой высокой оценке не помешало даже то, что Ломоносов математических работ не писал и высшей математикой не владел.
Михаил Ломоносов
Слайд 15В 1765 году опубликована «Теория движения твёрдых тел», а годом позже
В 1762 году на русский престол вступила Екатерина II, которая осуществляла политику просвещённого абсолютизма. Хорошо понимая значение науки как для прогресса государства, так и для собственного престижа, она провела ряд важных, благоприятных для науки преобразований в системе народного просвещения и культуры. Императрица предложила Эйлеру управление математическим классом, звание конференц-секретаря Академии и оклад 1800 рублей в год. «А если не понравится, — говорилось в письме её представителю, — благоволит сообщить свои условия, лишь бы не медлил приездом в Петербург».
Эйлер сообщил в ответ свои условия:
оклад 3000 рублей в год и пост вице-президента Академии;
квартира, свободная от солдатского постоя;
оплачиваемые должности для троих его сыновей, в том числе пост секретаря Академии для старшего.
Екатерина II
Слайд 1617 (28) июля 1766 года 60-летний Эйлер, его семья и домочадцы
К несчастью, после возвращения в Петербург у Эйлера образовалась катаракта левого глаза — он перестал видеть. Вероятно, по этой причине обещанный пост вице-президента Академии он так и не получил (что не помешало Эйлеру и его потомкам в течение почти ста лет участвовать в управлении Академией.
Леонард Эйлер
Однако слепота не отразилась на работоспособности учёного, он лишь заметил, что теперь будет меньше отвлекаться от занятий математикой. До обретения секретаря Эйлер диктовал свои труды мальчику-портному, который всё записывал по-немецки.
Слайд 17В эти же годы вышли трёхтомник «Диоптрика» (лат. Dioptrica, 1769—1771) о
Огромную популярность приобрели в XVIII веке, а отчасти и в XIX, эйлеровские «Письма о разных физических и философических материях, написанные к некоторой немецкой принцессе…» (1768), которые выдержали свыше 40 изданий на 10 языках (в том числе 4 издания на русском). Это была научно-популярная энциклопедия широкого охвата, написанная ярко и общедоступно.
Слайд 18В 1771 году в жизни Эйлера произошли два серьёзных события. В
Второе событие: в сентябре того же года, по особому приглашению императрицы, в Санкт-Петербург прибыл для лечения Эйлера известный немецкий окулист барон Вентцель. После осмотра он согласился сделать Эйлеру операцию и удалил с левого глаза катаракту. Эйлер снова стал видеть. Врач предписал беречь глаз от яркого света, не писать, не читать — лишь постепенно привыкать к новому состоянию. Однако уже через несколько дней после операции Эйлер снял повязку и вскоре потерял зрение снова. На этот раз — окончательно.
1772: «Новая теория движения Луны». Эйлер наконец завершил свой многолетний труд, приближённо решив задачу трёх тел.
В 1773 году по рекомендации Даниила Бернулли в Петербург приехал из Базеля ученик Бернулли, Николаус Фусс. Это было большой удачей для Эйлера. Фусс, одарённый математик, сразу же после приезда взял на себя заботы о математических трудах Эйлера. Вскоре Фусс женился на внучке Эйлера. В последующие десять лет — до самой своей смерти — Эйлер преимущественно ему диктовал свои труды, хотя иногда пользовался «глазами старшего сына» и других своих учеников.
Слайд 19В 1779 году опубликована «Всеобщая сферическая тригонометрия», это первое полное изложение
Эйлер активно трудился до последних дней. В сентябре 1783 года 76-летний учёный стал ощущать головные боли и слабость.
7 (18) сентября после обеда, проведённого в кругу семьи, беседуя с академиком А. И. Лекселем о недавно открытой планете Уран и её орбите, он внезапно почувствовал себя плохо. Эйлер успел произнести: «Я умираю», — и потерял сознание. Через несколько часов, так и не приходя в сознание, он скончался от кровоизлияния в мозг
Надгробие Л. Эйлера, гранитный саркофаг
«Здесь покоятся останки знаменитого во всём свете Леонарда Эйлера, мудреца и праведника. Родился в Базеле 4 апреля 1707 года, умер 7 сентября 1783 года»
Leonhardo Eulero —
Academia Petropolitana
Слайд 20Эйлер внес большой вклад в алгебру и теорию чисел, где его
Слайд 21Используя специально подобранную символику, Эйлер облегчил язык математики, сделал ее более
Современная тригонометрия с определением тригонометрических функций как отношений и с принятыми в ней обозначениями берет начало с эйлеровского «Введение».
Слайд 22Функция Эйлера ϕ(n) показывает, сколько натуральных чисел из отрезка [1, n-1]
Первая тысяча значений Первая тысяча значений ϕ(n)
Слайд 23Круги́ Э́йлера— геометрическая схема, с помощью которой можно изобразить отношения между
Задача
В воскресенье 19 учеников нашего класса побывали в планетарии, 10 – в цирке и 6 – на стадионе. Планетарий и
цирк посетили 5 учеников; планетарий и стадион-3; цирк и стадион -1. Сколько учеников в нашем классе, если никто не
успел посетить все три места, а три ученика не посетили ни одного места?
Слайд 24Прямая Эйлера может быть определена как прямая, проходящая через центр описанной
В треугольнике ABC ортоцентр H, центр U описанной окружности и центроид S лежат на одной «прямой Эйлера»
Уточнение теоремы Эйлера. Прямая Эйлера (красная) проходит через центр описанной окружности треугольника, его ортоцентр, центр тяжести и центр окружности девяти точек.
Слайд 25Теорема Эйлера о многогранниках: Для любого многогранника
где В – число вершин, Р – число ребер, Г – число граней.
С помощью этой теоремы можно доказать, что существует не более пяти видов правильных многогранников : тетраэдр, куб, октаэдр, додекаэдр и икосаэдр.
Куб Тетраэдр Октаэдр Икосаэдр Додекаэдр
Слайд 27 Комплексный логарифм - мнимая часть)
Современному понимание логарифмирования — как операции,
Логарифмическая функция
Слайд 28Задача о семи мостах Кёнигсберга
Издавна среди жителей Кёнигсберга была распространена такая
Эйлер формализовал её, сведя к задаче о существовании в графе (вершины которого отвечают частям города, разделённым протоками реки Преголя, а рёбра — мостам) циклического маршрута, проходящего по каждому ребру ровно один раз (в современной терминологии — эйлерова цикла). Решая последнюю задачу, Эйлер показал: для наличия эйлерова цикла в графе нужно, чтобы у каждой вершины её степень (число выходящих из вершины рёбер) была чётной (а в задаче о кёнигсбергских мостах это не так: степени равны 3, 3, 3 и 5
Слайд 29Дети математика так и остались в России. Старший сын, тоже талантливый
Внук, Александр Христофорович (1773-1849) стал генералом от артиллерии, героем Отечественной войны 1812 года.
Еще один потомок, правда вернувшийся на родину предков, в Швецию, Ханс Карл Август Симон фон Эйлер-Хельпин (1873-1964) стал известным биохимиком, иностранным членом Академии Наук СССР, лауреатом Нобелевской премии по химии за 1929 год.
Другую Нобелевскую премию, только уже в 1970 году, получил его сын, шведский биолог Ульф фон Ойлер (1905-1983).
Слайд 30Источники иллюстраций
Интернет :Google картинки - http://physiclib.ru, http://www.aif.ru, http://www.bourabai.kz,
Источники текстовой информации
https://ru.wikipedia.org/wiki/Эйлер_Леонард
http://provizorii.ru/index.php/Леонард_Эйлер
http://physiclib.ru/books/ Библиотека по физике . Эйлер и его воззрения.
http://www.aif.ru Леонард Эйлер: никогда не отвлекаться на внешние красоты, не связанные с математикой
http://www.eduspb.com ЭЙЛЕР Леонард (Euler Leonard)
Е.Ф. Литвинова. Леонард Эйлер. Его жизнь и научная деятельность. Жизнь замечательных людей. Биографическая библиотека Ф.Павленкова
В. Котек. Леонард Эйлер. Пособие для учителей. М. 1961
А.Я. Яковлев. Леонард Эйлер. Пособие для учащихся. Серия "Люди науки". М. "Просвещение". 1983



















![Презентация, Жизнь замечательных людей, Внеклассное мероприятие Леонард Эйлер Функция Эйлера ϕ(n) показывает, сколько натуральных чисел из отрезка [1, n-1] Функция Эйлера ϕ(n) показывает, сколько натуральных чисел из отрезка [1, n-1] имеют n только один общий делитель](/img/thumbs/dad8fc6ae4fd19f7efd8e656db002f79-800x.jpg)