- Главная
- Разное
- Образование
- Спорт
- Естествознание
- Природоведение
- Религиоведение
- Французский язык
- Черчение
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, фоны, картинки для презентаций
- Экология
- Экономика
Презентация, доклад Задания с параметром в ОГЭ
Содержание
- 1. Презентация Задания с параметром в ОГЭ
- 2. Некоторые типы заданий с параметрами
- 3. Что значит решить уравнение с параметром?
- 4. Решить уравнение Решение:При а=-3 уравнение не имеет
- 5. При каких значениях а следующее уравнение имеет
- 6. При каких значениях параметра k уравнение x2-6x+8=k
- 7. При каких значениях параметра а уравнение |2x+4|=ax+1
- 8. При каких значениях а уравнение |x+1| +
- 9. Найти все значения параметра а при которых
- 10. Решить уравнение ||х|-2|-|х-4|=аЗададим функцию а(х)= ||х|-2|-|х-4|
- 11. При каких значениях параметра m график функции
- 12. При каких значениях корни квадратного трехчлена действительны и оба больше ½)?
- 13. Расположение корней квадратного трехчлена
- 14. При каких значениях корни квадратного трехчлена действительны
- 15. Найти все действительные значения k , при
- 16. Для каждого действительного числа а решить уравнение
- 17. При каких значениях k верно следующее утверждение:
- 18. Для каждого значения a решить неравенство Решение:Простроим
- 19. Слайд 19
- 20. При каких значения параметра a уравнение имеет
- 21. Выяснить при каких значениях параметра a уравнение
Слайд 1
Задания с
параметром В ОГЭ
учитель Шадрина Татьяна Михайловна
МБОУ Городская гимназия
Слайд 2 Некоторые типы заданий
с параметрами в гиа
1.Решить уравнение, неравенство или
2.Определить количество корней уравнения при различных значениях параметра;
3.Найти все значения параметра, при которых уравнение
( неравенство, система) имеет единственное решение, ровно два решения, не имеет решений, выполняется при всех х и т.д.;
4. Найти все значения параметра, при которых данные уравнения или неравенства равносильны, одно является следствием другого, имеют хотя бы один общий корень и т.д.
5. Найти все значения параметра, при которых корни квадратного уравнения удовлетворяют поставленным условиям ( один корень меньше данного числа а, оба корня больше а и т. д .)
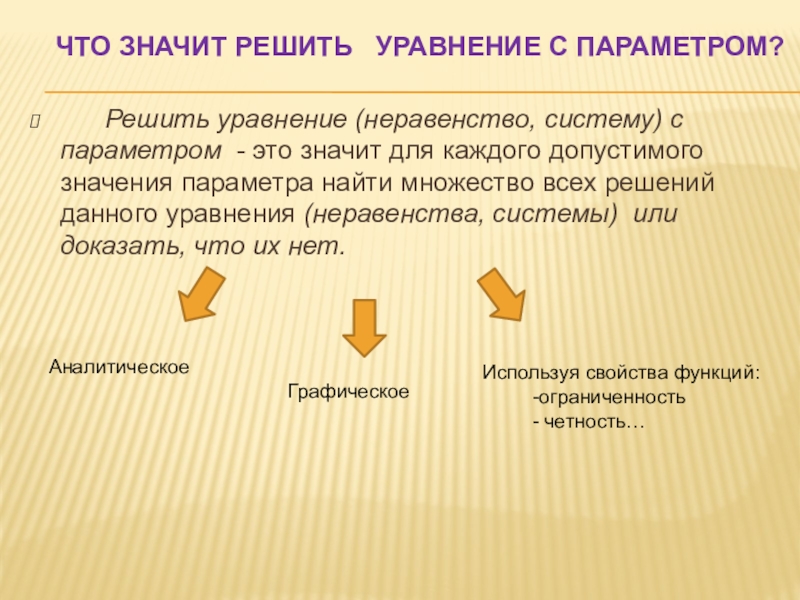
Слайд 3Что значит решить уравнение с параметром?
Решить уравнение
Аналитическое
Графическое
Используя свойства функций:
-ограниченность
- четность…
Слайд 4Решить уравнение
Решение:
При а=-3 уравнение не имеет решений
При а=4 уравнение не
При а≠-3, а≠4 уравнение имеет корень равный х=а.
Ответ:
нет решений при а=-3 и а=4
х=а, при а≠-3, а≠4.
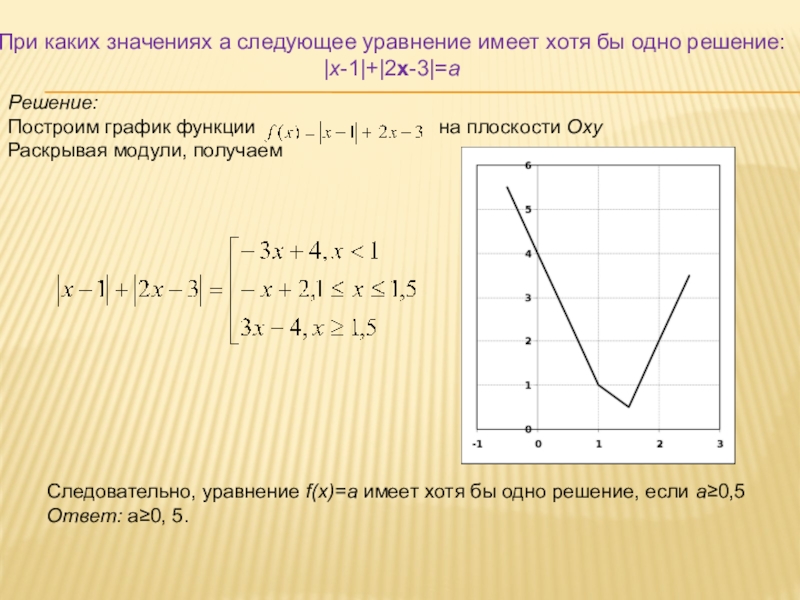
Слайд 5При каких значениях а следующее уравнение имеет хотя бы одно решение:
|x-1|+|2x-3|=a
Решение:
Построим график функции
на плоскости Oxy
Раскрывая модули, получаем
Следовательно, уравнение f(x)=a имеет хотя бы одно решение, если a≥0,5
Ответ: а≥0, 5.
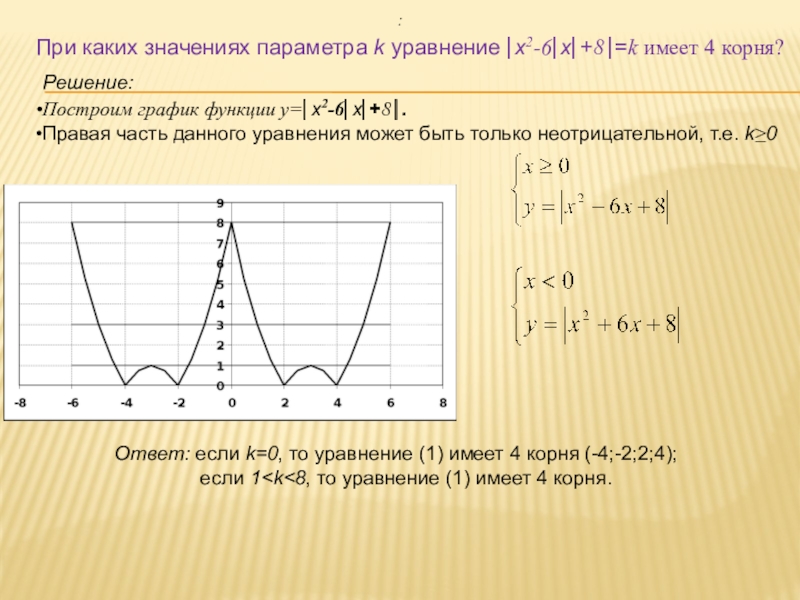
Слайд 6При каких значениях параметра k уравнение x2-6x+8=k имеет 4 корня?
Построим график
Правая часть данного уравнения может быть только неотрицательной, т.е. k0
:
Решение:
Ответ: если k=0, то уравнение (1) имеет 4 корня (-4;-2;2;4);
если 1
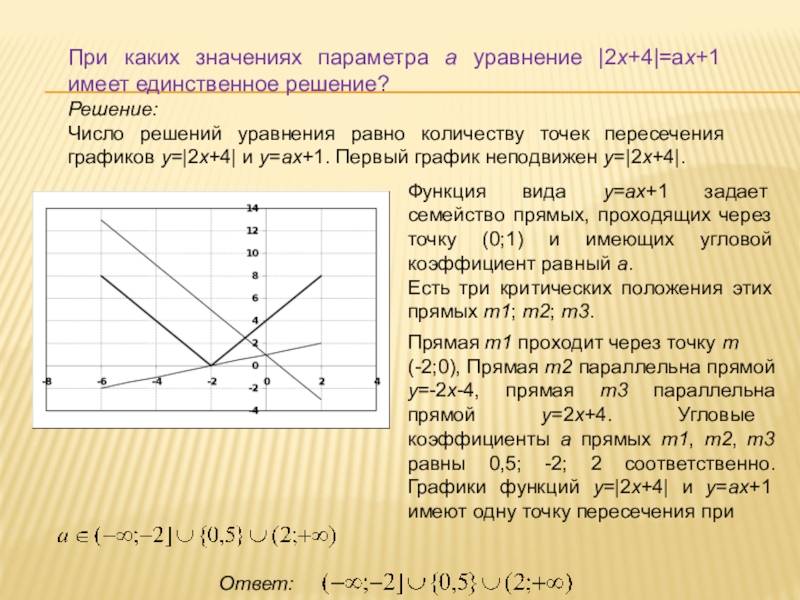
Слайд 7При каких значениях параметра а уравнение |2x+4|=ax+1 имеет единственное решение?
Решение:
Число решений
Функция вида у=ах+1 задает семейство прямых, проходящих через точку (0;1) и имеющих угловой коэффициент равный а.
Есть три критических положения этих прямых m1; m2; m3.
Прямая m1 проходит через точку m
(-2;0), Прямая m2 параллельна прямой у=-2х-4, прямая m3 параллельна прямой у=2х+4. Угловые коэффициенты а прямых m1, m2, m3 равны 0,5; -2; 2 соответственно. Графики функций y=|2x+4| и y=ax+1 имеют одну точку пересечения при
.
.
Ответ:
Слайд 8При каких значениях а уравнение |x+1| + |x-a|=3
имеет хотя бы
Решение:
Данное уравнение равносильно |x+1| -3 = -|x-a|. Воспользуемся методом графической интерпретации.
Построим график y=|x+1|-3
Функция вида
задает семейство графиков, получающихся из графика а функции y= -|x| сдвигом на а единиц вдоль оси Ox.
Уравнение имеет хотя бы одно решение при -4≤a≤2
Ответ: -4≤a≤2.
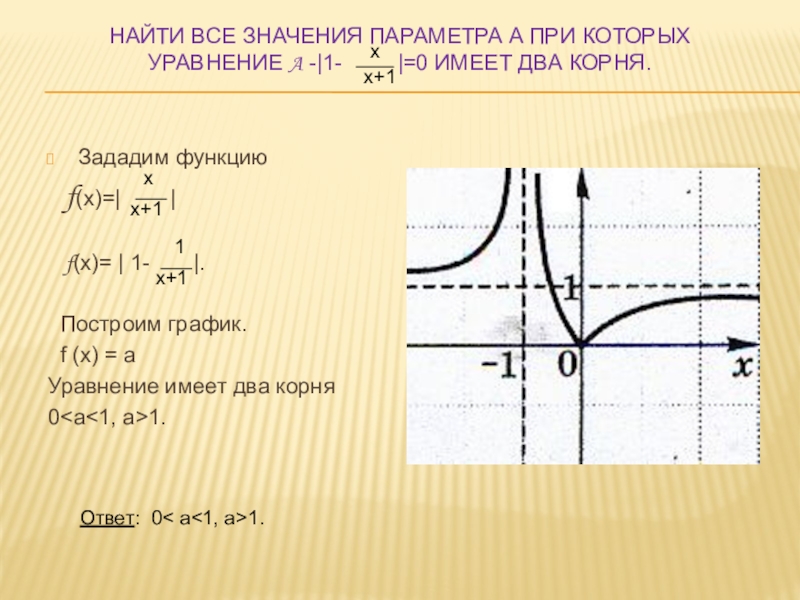
Слайд 9Найти все значения параметра а при которых уравнение a -|1-
Зададим функцию х х+1 х х+1 1 х+1 Ответ: 0< а<1, а>1. а
f(х)=| |
f(х)= | 1- |.
Построим график.
f (x) = a
Уравнение имеет два корня
0
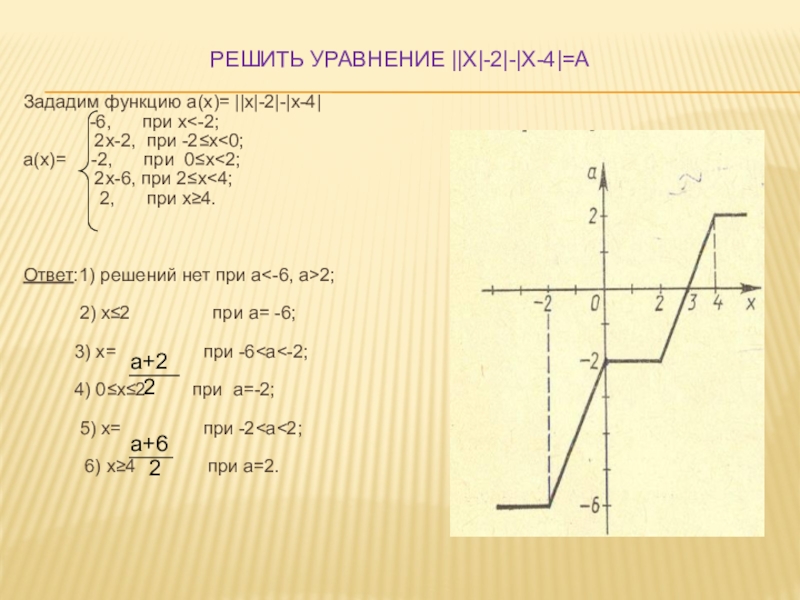
Слайд 10Решить уравнение ||х|-2|-|х-4|=а
Зададим функцию а(х)= ||х|-2|-|х-4|
2х-2, при -2≤х<0;
а(х)= -2, при 0≤х<2;
2х-6, при 2≤х<4;
2, при х≥4.
Ответ:1) решений нет при а<-6, а>2;
2) х≤2 при а= -6;
3) х= при -6<а<-2;
4) 0≤х≤2 при а=-2;
5) х= при -2<а<2;
6) х≥4 при а=2.
а+2
2
а+6
2
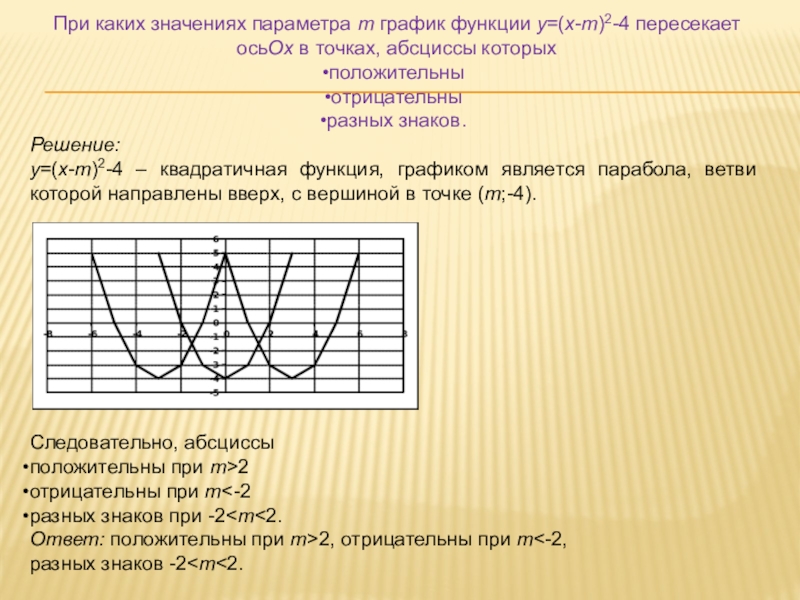
Слайд 11При каких значениях параметра m график функции y=(x-m)2-4 пересекает осьOx в
положительны
отрицательны
разных знаков.
Решение:
y=(x-m)2-4 – квадратичная функция, графиком является парабола, ветви которой направлены вверх, с вершиной в точке (m;-4).
Следовательно, абсциссы
положительны при m>2
отрицательны при m<-2
разных знаков при -2
разных знаков -2
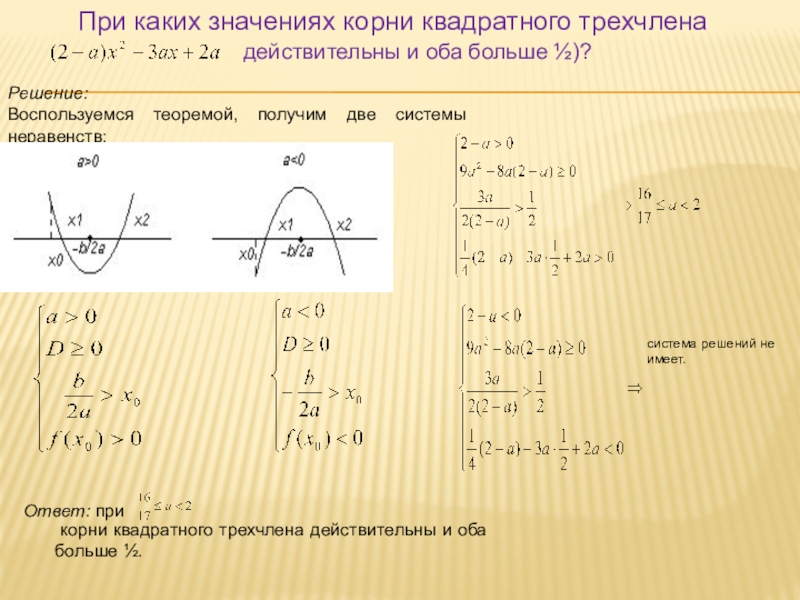
Слайд 14При каких значениях корни квадратного трехчлена
действительны и оба больше
Решение:
Воспользуемся теоремой, получим две системы неравенств:
система решений не имеет.
Ответ: при
корни квадратного трехчлена действительны и оба больше ½.
Слайд 15Найти все действительные значения k , при которых квадратный трехчлен
.
Решение:
Условие задачи выполняется тогда и только тогда, когда интервал будет расположен между корнями параболы, т.е. если
Подставляем значение 1 и 2 в данный трехчлен, получим систему
двух квадратных неравенств.
Решая систему, получим
Ответ:
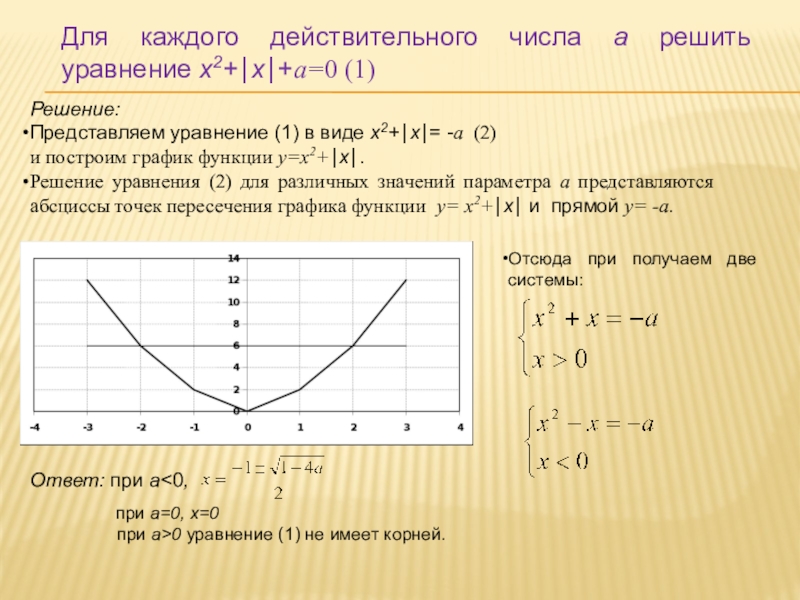
Слайд 16Для каждого действительного числа а решить уравнение х2+х+а=0 (1)
Решение:
Представляем уравнение (1)
и построим график функции у=х2+х.
Решение уравнения (2) для различных значений параметра а представляются абсциссы точек пересечения графика функции у= х2+х и прямой у= -а.
Отсюда при получаем две системы:
Ответ: при a<0,
при a=0, x=0
при a>0 уравнение (1) не имеет корней.
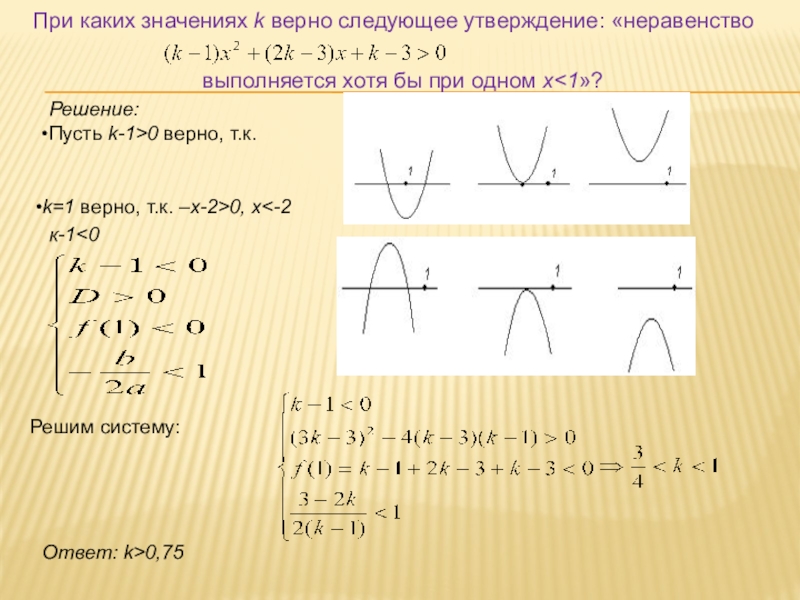
Слайд 17При каких значениях k верно следующее утверждение: «неравенство
выполняется хотя
Решение:
Пусть k-1>0 верно, т.к.
k=1 верно, т.к. –x-2>0, x<-2
Решим систему:
Ответ: k>0,75
к-1<0
Слайд 18Для каждого значения a решить неравенство
Решение:
Простроим график функций стоящих в
График функции
получается из графика функции
сдвигом вдоль оси Ox на a единиц и имеет три критических положения, соответствующих значением параметра a , равным -2; -1/4; 4 соответственно.
Исходному неравенству удовлетворяют координаты точек x, при которых график функций
расположен выше графика функции
. Абсциссы точек пересечения указанных графиков определяются из уравнения
.
Если
, то
Если
, то
Если
,то
Если
.
,то
Ответ:
Слайд 19
в зависимости от a.
Найти решение уравнения в случае, когда оно единственное.
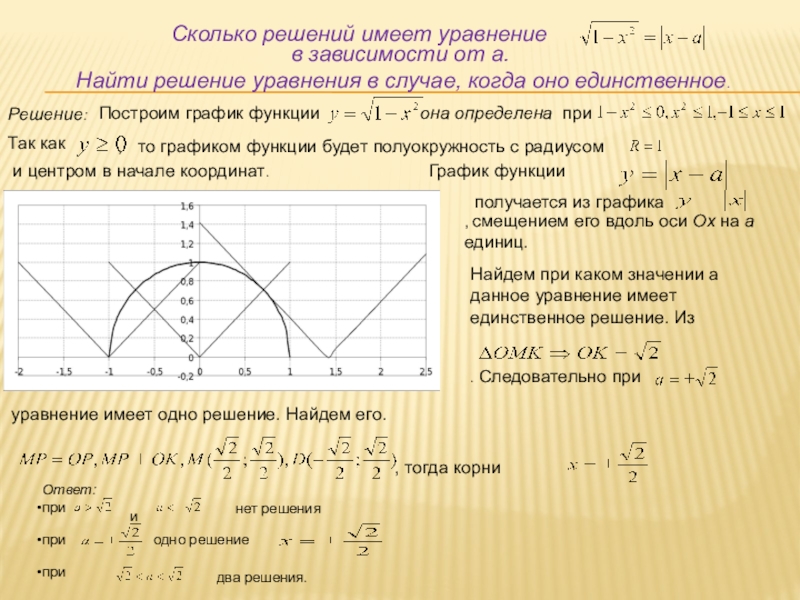
Решение:
Построим график функции
она определена при
Так как
, то графиком функции будет полуокружность с радиусом
и центром в начале координат.
График функции
получается из графика
, смещением его вдоль оси Ox на a единиц.
Найдем при каком значении a данное уравнение имеет единственное решение. Из
. Следовательно при
уравнение имеет одно решение. Найдем его.
, тогда корни
.
Ответ:
при
и
нет решения
при
одно решение
при
два решения.
Слайд 20При каких значения параметра a уравнение
имеет три решения?
Решение.
Пусть
,
по теореме обратной теореме Виета имеем:
Следовательно, данное уравнение равносильно совокупности уравнений
Так как второе уравнение имеет два решения, тогда уравнение имеет три решения тогда и толок тогда, когда уравнение (1) имеет одно решение, отличное от корней второго уравнения. Это возможно тогда, когда a=0.
Ответ: a=0.
Слайд 21Выяснить при каких значениях параметра a уравнение
имеет три различных
Решение:
Если
является корнем уравнения, то -
- корень уравнения, т.е. переменная в четной степени. Чтобы уравнение имело три корня, один из них должен равняться нулю, а два противоположных. Если
, то уравнение имеет вид
Проверим, достаточно ли этих значений а , чтобы уравнение имело три различных корня.
Если
то уравнение имеет вид
Если
,
то
Ответ: при
,
данное уравнение имеет три различных корня.