- Главная
- Разное
- Образование
- Спорт
- Естествознание
- Природоведение
- Религиоведение
- Французский язык
- Черчение
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, фоны, картинки для презентаций
- Экология
- Экономика
Презентация, доклад Задачи на оптимизацию
Содержание
- 1. Презентация Задачи на оптимизацию
- 2. Определяя точки минимума функции, ученик
- 3. Определяя точки минимума функции, ученик
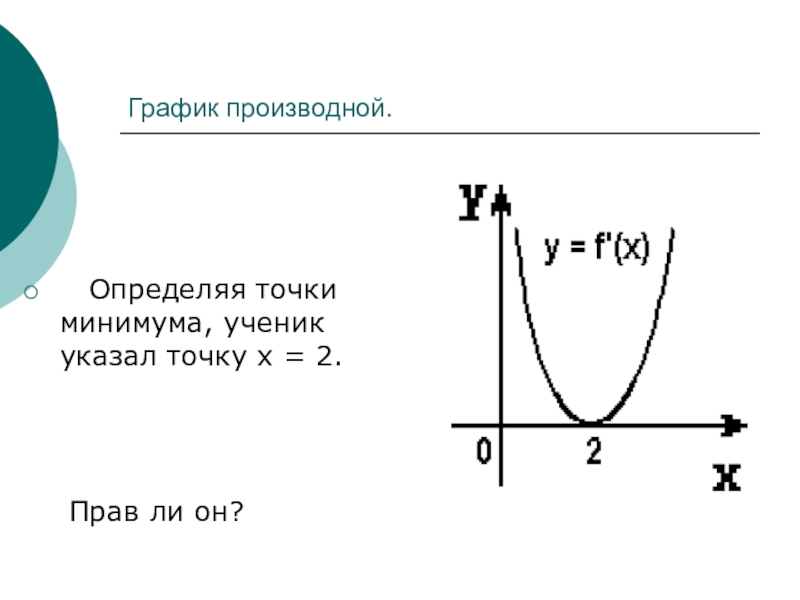
- 4. График производной. Определяя точки минимума, ученик
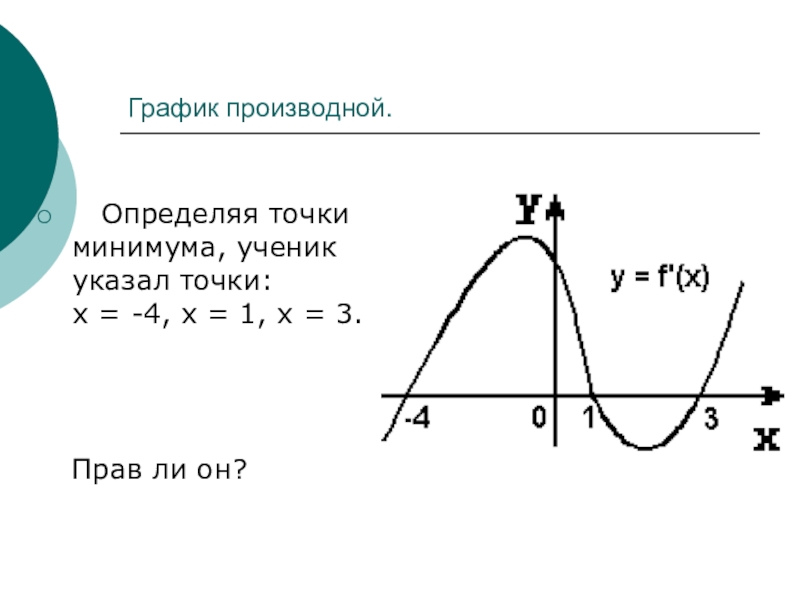
- 5. График производной. Определяя точки минимума, ученик
- 6. На промежутке (0;2) у`(x)
- 7. Является ли точка х = 2 критической для функции у(х), если D(y) = [-3;2]?
- 8. На отрезке [a;b] функция имеет
- 9. Непрерывная на отрезке [a;b] функция
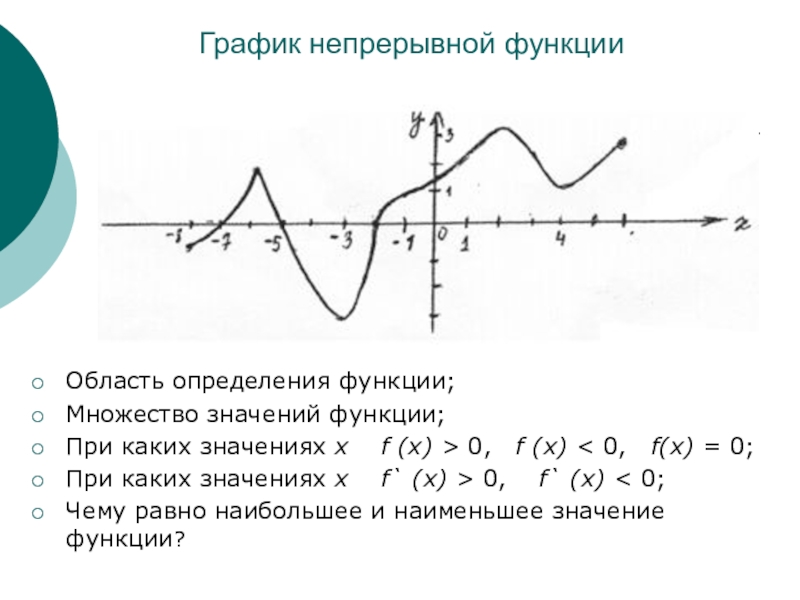
- 10. График непрерывной функцииОбласть определения функции; Множество
- 11. Алгоритм нахождения наибольшего и наименьшего значений функции.Найти
- 12. Проверка домашнего задания Найти наибольшее значение
- 13. Решение задачи V(x) = (12
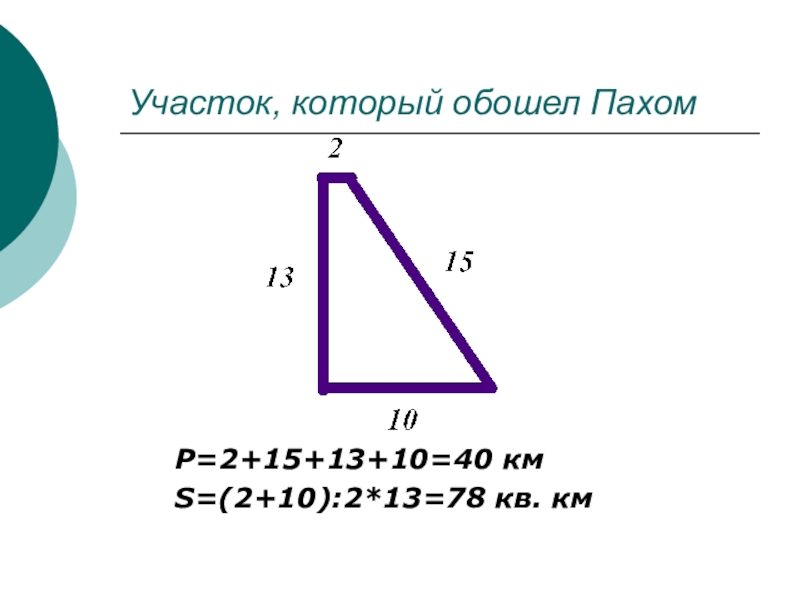
- 14. Л.Н. Толстой «Много ли человеку земли надо?»
- 15. Участок, который обошел ПахомP=2+15+13+10=40 кмS=(2+10):2*13=78 кв. км
- 16. «Особенную важность имеют те методы науки, которые
- 17. Задачи на оптимизацию. Оптимизация, (от лат. optimum- наилучший). Выбор наилучшего из возможных вариантов.
- 18. Цели урокаЗнать алгоритм решения практических задач на
- 19. Схема решения задач на оптимизациюСоставление математической модели выбирается
- 20. Периметр прямоугольника равен 40 см. Какую длину должны иметь стороны прямоугольника, чтобы площадь была наибольшей?
- 21. Задача: Периметр прямоугольника равен 40 см. Какую
- 22. Слайд 22
- 23. Проверка домашнего заданияПусть MN=X, тогда AM= (12-х)/2.
- 24. Слайд 24
- 25. Задача Открытый металлический бак с квадратным
- 26. Решение: Пусть х –
- 27. ЗадачаСтроители решили пристроить к стене школы физкультурный
- 28. Решение задач в группах.1 группа.
- 29. Ответы1 группа. (12; 12).2 группа. (12, 24, 18 )3 группа. (50, 100, 50)
- 30. Однажды в разговоре П.Л. Чебышев заметил: «В
- 31. Домашнее задание.1 группа – учебник:
Слайд 2
Определяя точки минимума функции, ученик нашел, при каких значениях
Прав ли он?
Слайд 3
Определяя точки минимума функции, ученик нашел те значения аргумента,
Прав ли он?
Слайд 5График производной.
Определяя точки минимума, ученик указал точки:
Прав ли он?
Слайд 6
На промежутке (0;2) у`(x) > 0,
Является ли точка х = 2 точкой максимума?
Слайд 8
На отрезке [a;b] функция имеет максимум, равный 5 и
Верно ли, что наибольшее значение функции равно 5, а наименьшее – равно 2?
Слайд 9
Непрерывная на отрезке [a;b] функция f(х) имеет единственную точку
Верно ли, что наибольшее значение функции на отрезке [a;b] равно 7?
Слайд 10 График непрерывной функции
Область определения функции;
Множество значений функции;
При каких
При каких значениях x f` (x) > 0, f` (x) < 0;
Чему равно наибольшее и наименьшее значение функции?
Слайд 11Алгоритм нахождения наибольшего и наименьшего значений функции.
Найти производную функции и критические
Вычислить значения функции в отобранных критических точках и на концах отрезка
Выбрать наибольшее и наименьшее значение функции
Слайд 12Проверка домашнего задания
Найти наибольшее значение функции V(x) =
При каком х достигается это значение?
Слайд 13 Решение задачи
V(x) = (12 – x) • х2
V(0)=0
V(8) =128
V(12)=0
Наибольшее значение функции
равно 128. Это значение функция принимает при х=8
Слайд 16
«Особенную важность имеют те методы науки, которые позволяют решать задачу, общую
П.Л. Чебышев
Слайд 17Задачи на оптимизацию.
Оптимизация,
(от лат. optimum- наилучший). Выбор наилучшего из
Слайд 18Цели урока
Знать алгоритм решения практических задач на оптимизацию;
Уметь применять алгоритм поиска
Осознать, насколько в жизни важны и необходимы математические знания.
Слайд 19Схема решения задач на оптимизацию
Составление математической модели
выбирается независимая переменная, через которую
Работа с моделью
находится наибольшее или наименьшее значение полученной функции
Ответ на вопрос задачи
по результатам, полученным в предыдущем пункте, записывается конкретный ответ на вопрос задачи
Слайд 20
Периметр прямоугольника равен 40 см. Какую длину должны иметь стороны прямоугольника,
Слайд 21Задача: Периметр прямоугольника равен 40 см. Какую длину должны иметь стороны
Решение: х 20 - х
Составляем математическую модель. Пусть х – ширина прямоугольника, тогда длина – 20 - х. Функция будет иметь следующий вид: S(x) = x • (20 - x) = 20x - x2 , где 0
Ответ:
Длина и ширина прямоугольника равны 10 см.
Вывод:
Наибольшую площадь среди четырехугольников при заданном периметре имеет квадрат
Слайд 23Проверка домашнего задания
Пусть MN=X, тогда AM= (12-х)/2. Функция примет вид V
Вывод:
объём коробки будет наибольшим при длине основания равном 8 см
Слайд 25Задача Открытый металлический бак с квадратным основанием должен вмещать 32 л
Слайд 26 Решение:
Пусть х – длина основания, тогда
S`=2х – 128/х2 2х3 - 128 = 0 х3 = 64 х = 4
х=4 – единственная точка минимума на отрезке, значит в ней функция принимает наименьшее значение.
Ответ: наименьшее количество металла потребуется для бака с размерами 4х4х2 дм.
Слайд 27Задача
Строители решили пристроить к стене школы физкультурный зал прямоугольной формы. Оказалось,
Какие размеры пристройки выбрать?
Слайд 28Решение задач в группах.
1 группа.
Сумма двух целых
2 группа.
Число 54 представьте в виде суммы трёх положительных слагаемых, два из которых пропорциональны числам 1 и 2, таким образом, чтобы произведение всех слагаемых было наибольшим.
3 группа.
Для стоянки машин выделили площадку прямоугольной формы, примыкающую одной стороной к стене здания. Площадку обнесли с трех сторон металлической сеткой длиной 200 м, и площадь ее при этом оказалась наибольшей. Каковы размеры площадки?
Слайд 30
Однажды в разговоре П.Л. Чебышев заметил: «В старину математические задачи задавали
Слайд 31Домашнее задание.
1 группа – учебник: задачи
2 и 3 группа - творческое задание. Составить вместе с родителями и оформить решение в тетради задачу на оптимизацию, с которой вам или вашим родителям пришлось столкнуться на практике.




![Презентация Задачи на оптимизацию Является ли точка х = 2 критической для функции у(х), если D(y) = [-3;2]? Является ли точка х = 2 критической для функции у(х), если D(y) = [-3;2]?](/img/tmb/5/479518/3978340f339c63d772849ca5fce761d5-800x.jpg)
![Презентация Задачи на оптимизацию На отрезке [a;b] функция имеет максимум, равный 5 и минимум, На отрезке [a;b] функция имеет максимум, равный 5 и минимум, равный 2, причем у(а)](/img/thumbs/a5ef07e3d3a77eaf9c415d3994e3de13-800x.jpg)
![Презентация Задачи на оптимизацию Непрерывная на отрезке [a;b] функция f(х) имеет единственную точку максимума Непрерывная на отрезке [a;b] функция f(х) имеет единственную точку максимума х=2, причём](/img/thumbs/230c6212212445e617c052f1c7715028-800x.jpg)
![Презентация Задачи на оптимизацию Алгоритм нахождения наибольшего и наименьшего значений функции.Найти производную функции и критические Алгоритм нахождения наибольшего и наименьшего значений функции.Найти производную функции и критические точки, лежащие внутри отрезка [a;b]Вычислить значения](/img/thumbs/4ca770b29e206cebab795100205f6a47-800x.jpg)